Jeżeli powstrzyma się od ruchu oscylatory z przesunięciem fazy miedzy nimi, spowoduje to deformacje pola falowego i przesunięcie węzłów względem oscylatorów.



Il. 107. Im większe przesunięcie fazy, tym większe względne przesunięcie oscylatorów i węzłów.
Węzły (dziury potencjału) odsuwają się od oscylatorów, podczas, gdy zmienione pole falowe wywiera siłę, zmuszają oscylatory do powrotu do węzłów. Gdy usunie się czynnik powstrzymujący, oscylatory zostaną popchnięte przez pole w kierunku do dziur potencjału. Jednak ze sztywnym przesunięciem fazowym jaką prędkość powinien posiadać układ, aby oscylatory pozostały w węzłach?
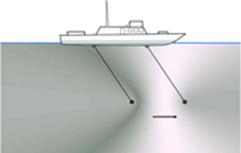
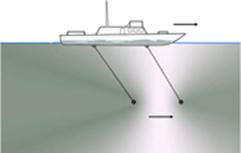
Il. 108. Jeżeli łódź jest przytrzymywana, będzie przyłożona do niej siła. b) Jeżeli łódź nie jest powstrzymywana, po wpływem tej siły zacznie przyspieszać, aż osiągnie pewną ustaloną prędkość.
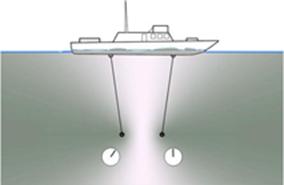
Il. 109. Oto, jak wygląda wyidealizowana sytuacja (brak oporów ośrodka), w której prędkość łodzi jest równa prędkości węzłów i oscylatorów.
Rozwiążmy problem, zaczynając od analizy stanu pola pomiędzy oscylatorami, i znalezienia warunków współgrania węzłów i oscylatorów.
Gdzie
l – dystans pomiędzy źródłami.
Rozwiązanie dla ogólnego przypadku:
- ,
- (4.03)
Rozwiazanie w badanym przypadku, gdy l = λst:
- ,
- (4.04)
Rozwiążmy problem odwrotny:
Załóżmy, że mamy dwa zgodne źródła fal elektromagnetycznych, między którymi powstaje elektromagnetyczna fala stojąca. Jakie powinno powstać miedzy nimi przesunięcie fazy, aby układ poruszał się z prędkością 8 km/s i 100 km/s, a źródła znajdowały się w węzłach?
Mamy:
V1 = 8 km/s; V2 = 100 km/s
c = 300000 km/s; π = 180°
Mamy obliczyć:
Δφ1 = ?, Δφ2 = ?
Rozwiązanie:
math>
Odpowiedź:
Δφ1 = 0,0048°; Δφ1 = 0,06°
Jak bardzo różnią się te wartości? Można to zobaczyć na ilustracji poniżej.


Il. 110. Górny obrazek pokazuje brak przesunięcia fazowego (Δφ = 0°), podcas gdy niższy pokazuje Δφ = 1°, co odpowiada prędkości V = 1666,6 km/s. Gołym okiem prawie nie widać różnicy.
Yuri N. Iwanow
Rytmodynamika – 4.06
Przetłumaczono z http://rhythmodynamics.com/rd_2007en.htm#4.06