Ukończyłem tłumaczenie pracy naukowej o nieznanym mi wcześniej zjawisku – „strahlu elektronowym”, rodzaju strumienia elektronów w wietrze słonecznym. Praca ta jest pierwszą z listy, którą planuję przetłumaczyć w ramach pogłębiania obecnego stanu wiedzy o wietrze słonecznym – w szczególności w poszukiwaniu przesłanek na wykrycie (lub przeoczenie) istnienia w nim prądu elektrycznego, postulowanego przez Model Elektrycznego Słońca.
Oryginalna praca jest dostępna na licencji CC tutaj: Exploring the Properties of the Electron Strahl at 1 AU as an Indicator of the Quality of the Magnetic Connection Between the Earth and the Sun
Tłumaczenie: PDF ODF. Układ trochę mi się rozjechał, wybaczcie. Chętnie przyjmę rady kogoś obeznanego w darmowym pakiecie biurowym.
Poniżej wersja w formacie HTML.
frontiers in Astronomy and Space Science
ORIGINAL RESEARCH
published: 05 March 2021
doi: 10.3389/fspas.2021.646443
Zgłębianie właściwości strahlu elektronów w odległości 1 jednostki astronomicznej jako wskaźnik jakości połączenia magnetycznego między Ziemią a Słońcem
Joseph E. Borovsky
Center for Space Plasma Physics, Space Science Institute, Boulder, CO, United States
Otwarty dostęp
Redaktor:
Daniele Telloni,
National Institute of Astrophysics
(INAF), Italy
Recenzjemci:
Daniel Verscharen,
University College London,
United Kingdom
Allan Macneil,
University of Reading, United Kingdom
Curt A. De Koning,
University of Colorado, Boulder, CO,
United States
*Kontakt:
Joseph E. Borovsky
jborovsky@spacescience.org
Specjalizacja:
Artykuł ten wysłano do
Space Physics,
sekcji czasopisma
Frontiers in Astronomy and
Space Sciences
Otrzymano: 26 grudnia 2020
Zaakceptowano: 29 stycznia 2021
Opublikowano: 05 marca 2021
Cytowanie:
Borovsky JE (2021) Exploring the
Properties of the Electron Strahl at 1
AU as an Indicator of the Quality of the
Magnetic Connection Between the
Earth and the Sun.
Front. Astron. Space Sci. 8:646443.
doi: 10.3389/fspas.2021.646443
W tym raporcie badane są niektóre własności strahlu (strumienia) elektronowego w odległości 1 AU w celu oceny strahlu o energii 272 eV jako wskaźnika jakości połączenia magnetycznego wiatru słonecznego w pobliżu Ziemi z Słońcem. Brak strahlu uznaje się za oznakę braku magnetycznego połączenia z koroną lub że strahl nie przetrwał do 1 AU z powodu rozpraszania. Jako wskaźniki dobrego połączenia magnetycznego mogą być wykorzystane zdarzenia słoneczno-energetyczno-elektronowe (SEE). Połączenie magnetyczne: badanie 216 impulsowych zdarzeń SEE pokazuje, że wszystkie one charakteryzują się silnymi strahlami. Intensywność strahli w 1 AU jest badana statystycznie dla różnych typów plazmy wiatru słonecznego: okazuje się, że strahl jest charakterystycznie słaby w plazmie obszaru odwracania. W plazmie regionu odwracania i innych powolnych wiatrów, czasowe zmiany intensywności strahlu w 1 AU badane są z rozdzielczością 64 s i ustalono statystyczne związki zmian strahlu z jednoczesnymi zmianami właściwości plazmy. Zmiany intensywności strahlu współwystępują z arkuszami prądu (nieciągłości kierunkowe) i silnymi zmianami w kierunku pola magnetycznego. Zmiany intensywności strahla w 1 AU są pozytywnie skorelowane ze zmianami entropii właściwej protonów, temperatury protonów i natężenia pola magnetycznego; zmiany intensywności strahlu są antyskorelowane ze zmianami gęstości liczbowej protonów, kąta pola magnetycznego w stosunku do kierunku pola magnetycznego w stosunku do kierunku spirali Parkera oraz stosunku liczbowo-gęstościowego alfa do liczby protonów. Zmniejszenie intensywności strahlu nie jest zgodne z oczekiwaniami dla prostego modelu rozpraszania turbulencyjno-gwizdowego. Zmniejszenie intensywności strahlów są w niewielkim stopniu zgodne z oczekiwaniami dla rozpraszania Coulomba, jednakże najsilniejsze zaobserwowane korelacje między plazmą a zmianami są niezwiązane z rozpraszaniem Coulomba i rozpraszaniem gwizdowym. Implikacje analizy zmian intensywności strahla są takie, że zmiana w kierunku pola magnetycznego przy zmianie strahla reprezentuje zmianę połączenia magnetycznego z koroną, co skutkuje inną intensywnością strahla i innymi właściwościami plazmy. Pozostaje pytanie: Czy brak strahla elektronowego reprezentuje magnetyczne odłączenie od Słońca lub słabe źródło strahlu w jakimś regionie korony?
Słowa kluczowe: wiatr słoneczny, heliosfera, korona, strahl, pogoda kosmiczna
Wprowadzenie
Znajomość połączeń magnetycznych pomiędzy Ziemią a Słońcem jest pożądana z kilku powodów: np. 1) aby uzyskać globalne zrozumienie struktury magnetycznej heliosfery, (np McComas et al., 1989 [67]; Crooker et al., 2002; Crooker and Pagel, 2008 [29]; Crooker and Owens, 2012 [28]; Lockwood, 2013 [60]; Viall and Borovsky, 2020 [99]), 2) dla zrozumienia zdarzeń związanych z energetycznymi cząstkami Słońca (protonami i elektronami) oraz ich transportem (Mazur et al., 2000 [65]; Chollet and Giacalone, 2011 [22]; Trenchi et al., 2013 [95]), oraz 3) dla oceny prawdopodobieństwa, że Ziemia będzie lub nie będzie poddana zdarzeniu z energetycznymi cząstkami.
Jedną z obiecujących metod oceny łączności magnetycznej pomiędzy wiatrem słonecznym w pobliżu Ziemi a Słońcem jest interpretacja obserwacji strumienia elektronów w wietrze słonecznym w pobliżu Ziemi. Strumień (strahl) elektronów to wiązka elektronów, pochodzących z korony słonecznej, wyrównana z polem magnetycznym, która rozchodzi się od Słońca (Feldman et al., 1976 [31]; Pilipp et al., 1987 [79]; Maksimovic et al., 2005 [64]). Silny strahl jest sygnaturą dobrego połączenia magnetycznego ze Słońcem; brak strahlu został historycznie zinterpretowany jako oznaka albo 1) braku połączenia magnetycznego ze Słońcem (McComas et al., 1989 [67]; Gosling et al., 2005 [41]) albo 2) strahl nie przetrwał drogi od Słońca do obserwatora (Pagel et al., 2005a [74]; Crooker and Pagel, 2008 [29]; Chollet et al., 2010 [23]).
W niniejszej pracy zmierzono intensywność strumienia elektronów o energii 272 eV. Lin i Kahler (1992) [59] zbadali szereg zdarzeń, które zostały uznane za magnetyczne rozłączenia przez brak niskoenergetycznego strahlu i stwierdzili obecność strahli o wyższej energii (2 keV-8.5 keV), poddając w wątpliwość czy brak strahli o niższej energii jest wskaźnikiem magnetycznego odłączenia od Słońca. Jednakże Gosling et al., (2005) [41] zbadali przypadki rozłączenia magnetycznego rekoneksyjnego wyczerpaniare i stwierdzili, że mieszanie się elektronów z halo może sprawiać wrażenie, że mamy do czynienia z bardziej energetycznym strahlem, nawet jeśli te linie pola magnetycznego były zdecydowanie odłączone od Słońca (Zobacz również analizę Crookera i Pagela (2008) [29]).
W odległości 1 AU od Słońca, intensywność elektronowego strahlu zmienia się na wielu skalach czasowych, z nagłymi skokami intensywności strahlu, które obserwuje się jako współwystępujące z silnymi arkuszami prądowymi (magnetycznymi nieciągłościami kierunkowymi) (Gosling et al., 2004a [39]; Borovsky, 2020a [14],b [15]). Stąd, czasowe skoki intensywności strahla są związane z nagłymi zmianami orientacji pola magnetycznego.
Niniejszy raport bada niektóre właściwości strumienia elektronów, które wpływają na możliwość oceny połączenia magnetycznego między Ziemią a Słońcem, wykorzystując obserwacje strumienia w wietrze słonecznym w pobliżu Ziemi. W sekcji Strahl elektronowy i rodzaje plazmy wiatru słonecznego badana jest zależność intensywności strahlu od rodzaju plazmy wiatru słonecznego. W Impulsywne zdarzeniach SEE, strahl elektronowy i typ plazmy badana jest intensywność strahlu elektronowego w 1 AU podczas impulsowych zdarzeń słoneczno-energetyczno-elektronowych (SEE), czyli w czasie, gdy musi istnieć dobre połączenie magnetyczne między Ziemią a Słońcem. W Analiza strahlu, nagłe zmiany w intensywności elektronowego strahla w 1 AU są badane statystycznie w odniesieniu do nagłych zmian innych parametrów plazmy, a wyniki statystyczne są dyskutowane w odniesieniu do pomysłów na zniszczenie strahla przez rozpraszanie Coloumba oraz testowane jest rozpraszanie gwizdowo-turbulencyjne. Dyskusja: interpretacja zmian intensywności strahla, ocena połączenia Słońce-Ziemia i przyszłość zawiera omówienie 1) interpretacji zmian intensywności strahla, 2) ocenę zdolności do określenia magnetycznego połączenia Słońce-Ziemia oraz 3) sugestie dotyczące przyszłych badań.
Strahl elektronowy i rodzaje plazmy wiatru słonecznego
Różne rodzaje plazmy słonecznej są emitowane do heliosfery z różnych typów regionów na obracającym się Słońcu. Te różne typy plazmy mają systematycznie różniące się parametry w 1 AU, (np. entropia właściwa protonów, prędkość, stosunek ładunków ciężkich jonów, prędkość Alfvena, itp.), co pozwala skategoryzować wiatr słoneczny na różne typy plazmy (por. Neugebauer et al., 2003 [72], 2016 [71]; Reisenfeld et al., 2003 [81]; Zhao et al., 2009 [109]; Xu and Borovsky, 2015 [108]; Camporeale et al., 2017 [21]; Veselovsky et al., 2018 [98]; Li et al., 2020 [58]; Amaya et al., 2020 [1]; Heidrich-Meisner et al., 2020 [44]; Bloch et al., 2020 [7]). Jedną z charakterystycznych różnic pomiędzy różnymi typami plazmy na wysokości 1 AU jest intensywność strumienia elektronów (Borovsky, 2018 [13]). Na ilustracji 1 ukazana jest uśredniona godzinowo intensywność strahlu elektronowego, zmierzona przez instrument SWEPAM (McComas et al., 1998 [66]) na sondzie kosmicznej ACE na wysokości L1 przed Ziemią. Składa się ona z czterech typów plazmy wiatru słonecznego w schemacie kategoryzacji plazmy Xu i Borovsky’ego (2015) [108]. I272 jest logarytmem o podstawie 10 gęstości fazowo-przestrzennej f272 (w jednostkach s2cm-5) strumienia elektronów w kierunku dominującym (równolegle do B lub antyrównolegle do B) przy energii 272 eV, zmierzonej przez ACE SWEPAM (Patrz: Borovsky. (2017) [12] dla dyskusji tworzenia uśrednionego godzinowo indeksu I272.). Na ilustracji 1 szara przerywana krzywa to rozkład występowania uśrednionej godzinowo intensywności strahlu I272 dla wszystkich danych w latach 1998-2013. Pozostałe cztery krzywe to rozkłady występowania uśrednionego godzinowo natężenia strahla w czterech typach plazmy wiatru słonecznego: plazma pochodząca z dziur koronalnych (czerwony), plazma pochodząca z pasa wstęgowego (zielony), plazma z regionu sektorowa zawracania (fioletowy) oraz plazma wyrzutowa (niebieski). Plazma wyrzutowa (niebieski) ma systematycznie bardziej intensywny strahl, plazma regionu sektorowo zawracania (fioletowy) ma systematycznie słabszy strahl, a plazma pochodząca z dziury koronalnej (czerwony) i plazma pochodząca z pasa wstęgowego (zielony) mają bardziej typowe wartości natężenia strahla.
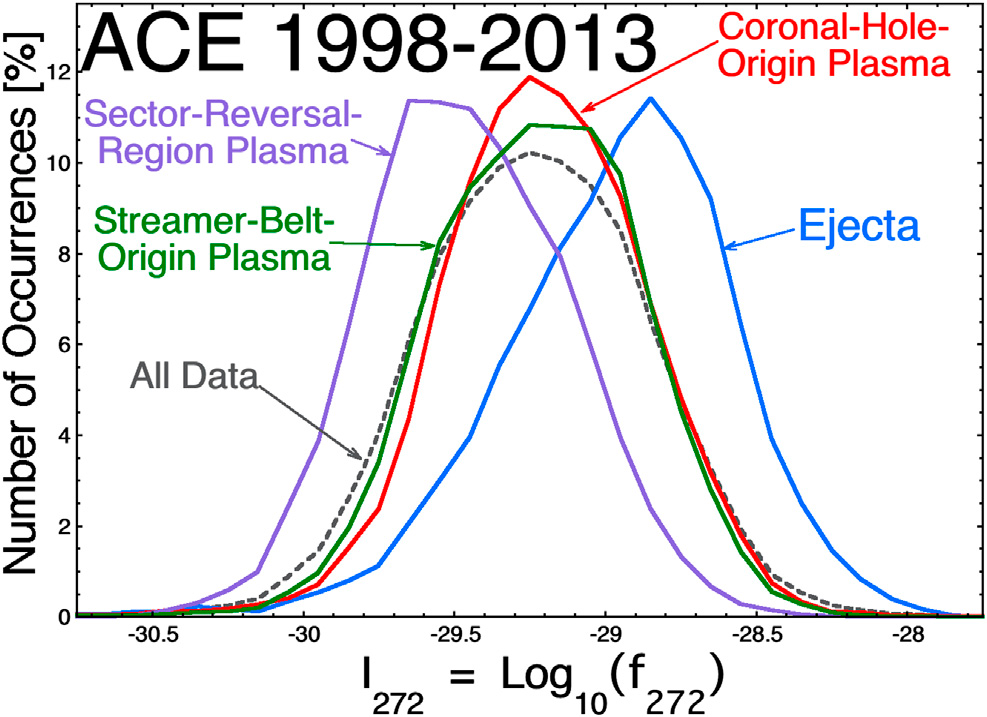
Ze względu na mocne intensywności strahlu na rysunku 1, (np. większe niż ∼ -29.75), można założyć, że plazma pochodząca z dziur koronalnych, pasa wstęgowego i wyrzutów w 1 AU jest, ogólnie rzecz biorąc, dobrze połączona magnetycznie ze Słońcem. Nie można tego zakładać dla plazmy regionu sektora zawracania, która na rysunku 1 ma zakres intensywności mogący być dość słabym, (np. mniejszy niż -29.75). W literaturze omawiane są dwa źródła plazmy regionu sektora zawracania. Pierwszym z nich jest rozłączenie pola magnetycznego spowodowane rekoneksją pomiędzy otwartym strumieniem po obu stronach odnogi strumienia (Wang et al., 1999 [104]; Sanchez-Diaz et al., 2019 [86]; Lavraud et al., 2020 [53]), co skutkuje emisją plam plazmy w rejonie strumień-odgałęzienie. Odłączenia z pewnością spowodują zmniejszenie intensywności strahla. Drugim źródłem jest rekoneksja wymienna pomiędzy otwartymi liniami pola i zamkniętymi pętlami streamerów (Wang et al., 2000 [105]; Crooker et al., 2004 [27]; Rouillard et al., 2020 [84]). Pojedyncze zdarzenia rekoneksji wymiennej, które zmieniają połączenie magnetyczne w pętle o różnych wysokościach i temperaturach elektronowych, prawie na pewno spowodują zmianę intensywności strahlu. Plazma w regionie sektora zawracania zawiera takie cechy, jak plamy i pufy w kształcie odgałęzień strumieni (Wang et al., 2000 [105]; Bemporad et al., 2005 [3]; Sheeley et al., 2009 [89]; Rouillard et al., 2010 [83]; Sheeley and Rouillard, 2010 [90]; Foullon et al., 2011 [34]) oraz okresowe struktury gęstości (Viall et al., 2010 [101]; Viall and Vourlidas, 2015 [102]), które są interesujące ze względu na ich wpływ na Ziemię (Kepko and Spence, 2003 [47]; Viall et al., 2009 [100]; Kepko and Viall, 2019 [49]). Te struktury plazmy w obszarze sektora zawracania mogą być związane z odłączeniami magnetycznymi od Słońca (Wang et al., 1999 [104]; Kepko et al., 2016 [48]). W sąsiedztwie heliosferycznego arkusza prądowego w plazmie sektora zawracania występują również zdarzenia rekoneksyjne-dyskoneksyjne (np. Gosling et al., 2005 [41]; Lavraud et al., 2009 [54], 2020 [53]; Sanchez-Diaz et al., 2019 [86]). Na podstawie słabszego strahla, plazma pochodząca z pasa wstęgowego jest najbardziej prawdopodobnym typem wiatru słonecznego, który jest słabo związany ze Słońcem.

Innym możliwym wskaźnikiem magnetycznego połączenia ze Słońcem jest to, czy pole magnetyczne w plazmie ma orientację spirali Parkera, czy nie. Plazma, która jest stale emitowana z danego miejsca na Słońcu, będzie miała w przybliżeniu pole magnetyczne o orientacji Parkera (Parker, 1958 [76]; Fisk, 2001 [32]; Georgieva et al., 2005 [37]); plazma emitowana impulsywnie, która może zawierać odłączenia magnetyczne, nie musi mieć pola magnetycznego o orientacji Parkera. Nawet dla stale emitowanego wiatru słonecznego może wystąpić niedokręcenie (np. Gosling and Skoug, 2002 [42]; Murphy et al., 2002 [69]; Riley and Gosling, 2007 [82]) lub przekręcenie (np. Smith and Bieber, 1991 [91]; Bruno and Bavassano, 1997 [18]) spirali Parkera, spowodowane przez wielkoskalowe ściśnięcia i rozrzedzenia, wokół kierunku spirali Parkera zawsze występują również duże fluktuacje kierunku pola magnetycznego (Ness and Wilcox, 1966 [70]; Forsyth et al., 1996 [33]; Burlaga and Ness, 1997 [20]; Borovsky, 2010 [10]). Na rysunku 2 pogrupowano uśredniony godzinowo kąt pomiędzy orientacją linii pola magnetycznego w wietrze słonecznym na Ziemi a kierunkiem spirali Parkera, przy czym kierunek spirali Parkera jest obliczany co godzinę przy użyciu uśrednionej godzinowo prędkości wiatru słonecznego (Ta orientacja linii pola nie uwzględnia znaku B ani nie bierze pod uwagę znaku B w stosunku do struktury sektora w kierunku do lub od). Wykorzystano zbiór danych OMNI (King and Papitashvili, 2005 [50]) dla lat 1963-2013. Na rysunku 2 rozkład wartości typu dziur koronalnych (krzywa czerwona) jest najbardziej wyrównany do spirali Parkera, a rozkład wartości typu obszaru sektora zawracania (krzywa fioletowa) jest najmniej wyrównany do spirali Parkera. Zauważmy, że z powodu fluktuacji kierunku pola magnetycznego wokół średniego kierunku Parkera-spirali, chwilowy kierunek pola magnetycznego (i uśredniony godzinowo kierunek pola) rzadko jest dokładnie wyrównany ze spiralą Parkera (Borovsky, 2010 [10]). Fakty 1) że pole magnetyczne jest mniej zorientowane na spiralę Parkera w plazmie regionu sektora zawracania i 2) że intensywność strahla jest mniejsza w plazmie regionu sektora zawracania wzmacniają koncepcję, że intensywność strahla i orientacja pola mogą być wskaźnikami dobrego lub słabego połączenia magnetycznego ze Słońcem. Jak zobaczymy w Analizie Strahla, intensywność strahla i kąt pola magnetycznego od spirali Parkera są słabo antyskorelowane w wietrze słonecznym w odległości 1 AU.
Impulsywne zdarzeniach SEE, strahl elektronowy i typ plazmy
Impulsowe energetyczne wydarzenia słoneczne (SEE) w odległości 1 AU są związane z rentgenowskimi rozbłyskami słonecznymi (np. Kallenrode and Svestka, 1994 [46]; Cliver and Ling, 2007 [24]) lub zdarzeniami w pobliżu Słońca (Li et al., 2013 [57]) i przyspieszonymi w pobliżu Słońca elektronami, podróżującymi wzdłuż pola magnetycznego wiatru słonecznego do sondy pomiarowej w odległości 1 AU. Jeśli można założyć, że impulsowe zdarzenia SEE są dobrymi wskaźnikami magnetycznej łączności ze Słońcem, to badanie intensywności strahla podczas wczesnych okresów impulsowych zdarzeń SEE vs. intensywność strahla, gdy zdarzenia SEE nie są widoczne, może być testem możliwości wykorzystania intensywności strahla jako miernika magnetycznej łączności ze Słońcem. Dobra łączność ze Słońcem może być ważnym założeniem dla impulsowych zdarzeń SEE (por. rysunek 2.3b Reamesa (1999) [80]) lub może nim nie być (por. rysunek 6 Wibberenza i Cane’a (2006) [107]).
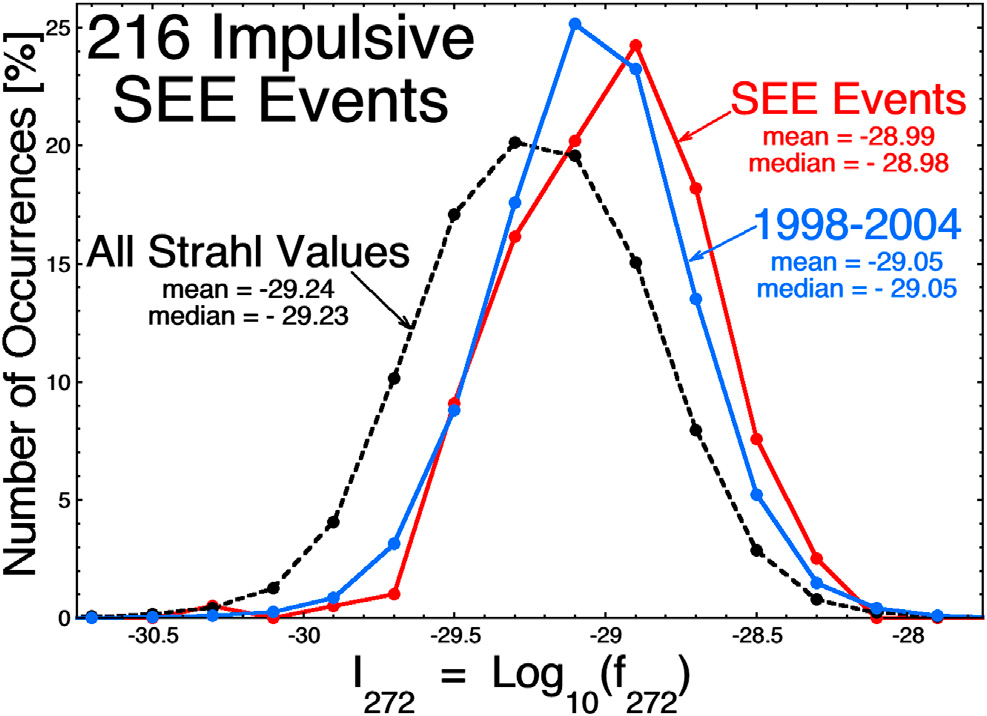
Ilustracja 4: Wykreślono rozkład intensywności strahlu dla 216 impulsowych zdarzeń SEE (czerwona krzywa). Wykreślono również rozkład występowania uśrednionych godzinowo natężeń strahlu w maksimum słonecznym 1998-2004 (krzywa niebieska) oraz dla sumy z lat 1998-2013 (krzywa czarna przerywana). Zakładając, że zdarzenia SEE są dobrze połączone ze Słońcem we wczesnym okresie, do zbadania innych warunków dobrego połączenia magnetycznego użyto 216 impulsowych zdarzeń bliskich Ziemi SEE z katalogu Wang et al., (2012) [106]: konkretnie, 216 zdarzeń w katalogu, które miały szczytowe energie kinetyczne elektronów 310 keV lub wyższe.
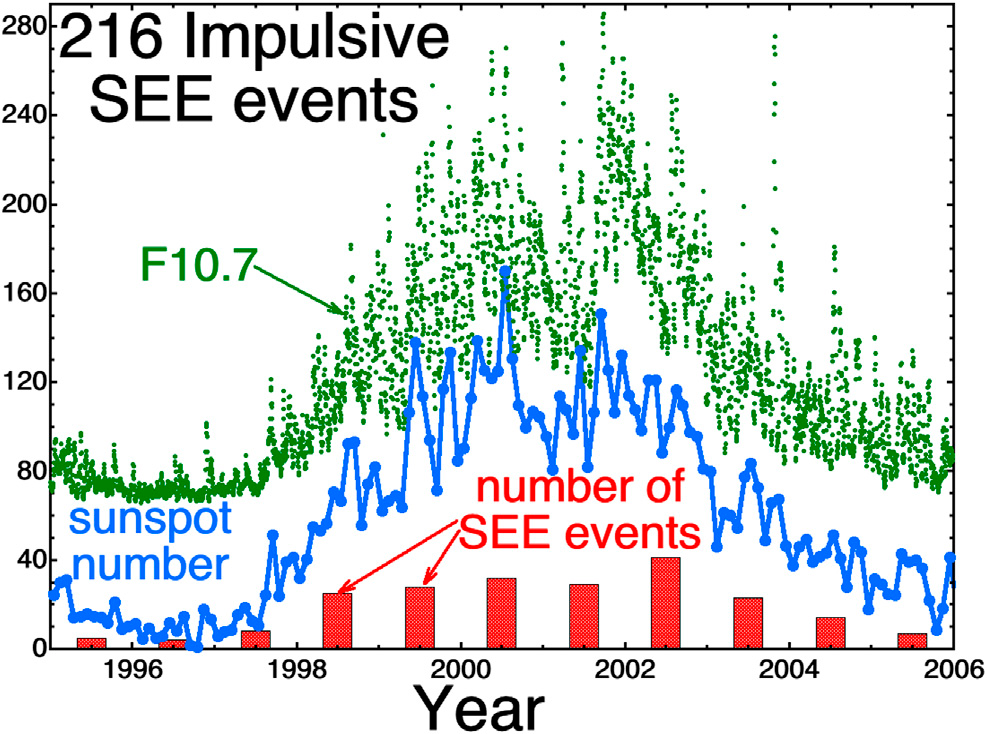
Na ilustracji 3 rozkład 216 zdarzeń SEE względem czasu jest wykreślony jako czerwone słupki, wraz z miesięczną liczbą plam słonecznych (niebieski) i dziennym uśrednionym strumieniem F10.7 (zielony). Jak można było się spodziewać, ponieważ zdarzenia SEE są związane z rozbłyskami słonecznymi, występowanie zdarzeń SEE jest skoncentrowane podczas maksimum słonecznego.
Na ilustracji 4 czerwona krzywa przedstawia rozkład występowania natężeń strahlu elektronowego przy Ziemi podczas 216 zdarzeń SEE przy użyciu uśrednionych godzinowo wartości natężeń strahlu z ACE SWEPAM. Czarna przerywana krzywa kreśli rozkład natężeń strahla dla lat 1998-2013, a niebieska krzywa kreśli rozkład dla przedziału maksimum słonecznego 1998-2004 (który jest również wykreślony na ilustracji 1). Stąd prawdopodobnie nie istnieją zdarzenia SEE przy Ziemi, które zostały pominięte, ponieważ Ziemia nie była magnetycznie połączona ze Słońcem: wydaje się, że Ziemia ma tendencję do posiadania dobrych połączeń magnetycznych podczas maksimum słonecznego. Jak widać na ilustracji 4, intensywności strahlu dla 216 zdarzeń SEE są mocne w porównaniu z czarnym rozkładem dla wszystkich czasów w latach 1998-2013. Można by pomyśleć, że strahl elektronowy powinien być intensywny, gdy obecne są energetyczne elektrony słoneczne, ponieważ są to dwie energie z tej samej funkcji rozkładu elektronów, ale tak nie jest: strahl jest reprezentacją temperatury elektronów koronalnych (Bercic et al., 2020 [5]; Boldyrev et al., 2020 [8]), a energetyczne elektrony słoneczne są produkowane przez specyficzne czasowe procesy przyspieszania (Kallenrode and Svestka, 1994 [46]; Cliver and Ling, 2007 [24]; Liet al., 2013 [57]). Również dla wczesnych etapów impulsywnych zdarzeń SSE, elektrony 272 eV z obserwowanego strahla na 1 AU opuściły Słońce ponad 4,3 h przed wystąpieniem rozbłysku.
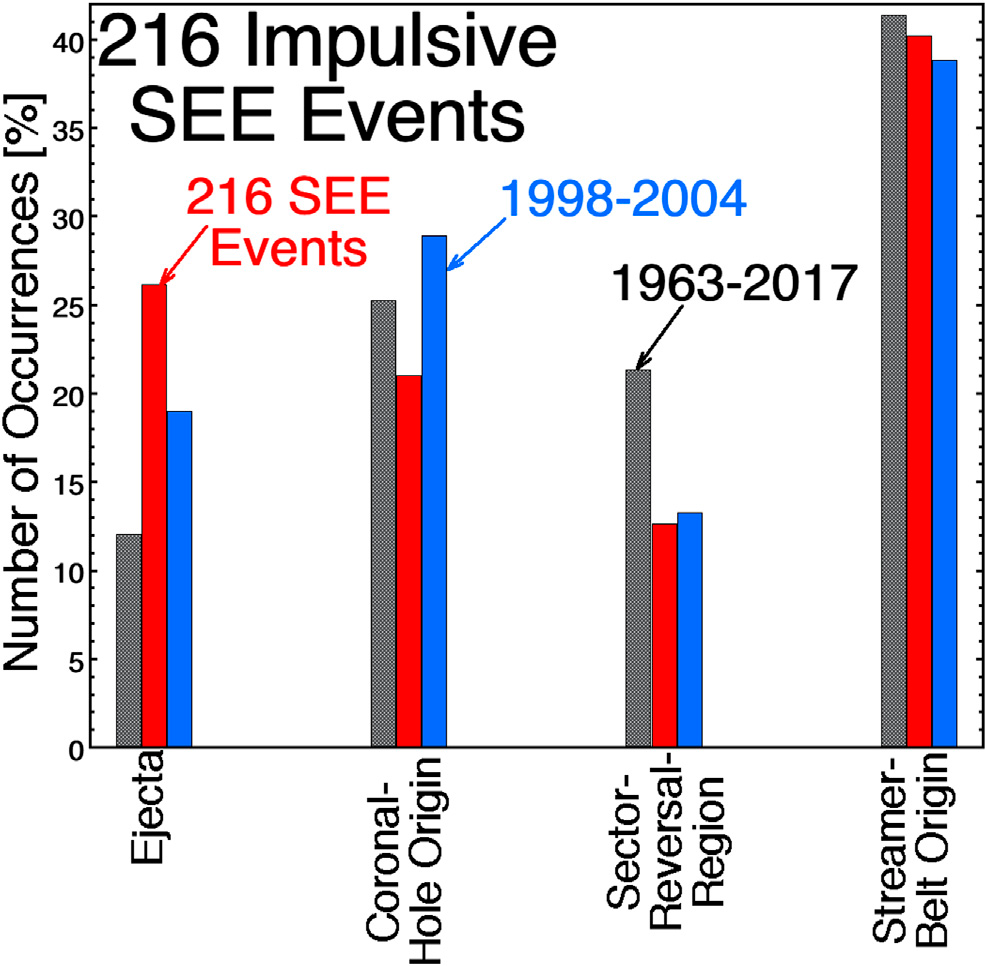
Na ilustracji 5, Używając schematu kategoryzacji Xu i Borovsky’ego (2015) [108], typ plazmy wiatru słonecznego, w którym znalazła się Ziemia, gdy zaobserwowano każde z 216 zdarzeń SEE, zaznaczono jako czerwone słupki; zaznaczono też plazmę dla przedziału maksimum słonecznego 1998-2004 (niebieskie słupki, po prawej) i dla całej bazy danych wiatru słonecznego 1963-2017 OMNI2 (czarne słupki, po lewej). Przy słabej statystyce, która podzieliła 216 zdarzeń SEE na cztery pule, rozkład występowania typów plazmy dla 216 zdarzeń SEE (czerwony) nie jest niespójny z rozkładem występowania typów plazmy dla maksimum słonecznego (niebieski): rozkład występowania SEE jest nieco wyższy dla plazmy wyrzutowej i nieco niższy dla plazmy pochodzącą z dziury koronalnej.
Analiza strahlu
Odłączenie magnetyczne od Słońca zostało wskazane przez strzępy strumienia cieplnego (brak strahla elektronowego), chociaż argumentowano, że nie wszystkie strzępy są odłączeniami magnetycznymi(por. Lin and Kahler, 1992 [59]; Pagel et al., 2005a [74]; Crooker and Pagel, 2008 [29]; Chollet et al., 2010 [23]). Interesująca jest interpretacja, czy obecność lub brak elektronowego strahlu w 1 AU wskazuje na obecność lub brak magnetycznego połączenia ze Słońcem, czy też brak strahlu jest spowodowany rozproszeniem strahlu pomiędzy Słońcem a 1 AU. Aby o tym poinformować, badane są nagłe zmiany intensywności strahlu elektronowego w 1 AU i porównywane z innymi jednoczesnymi zmianami, aby określić, czy zmiany intensywności strahlu w 1 AU mogą być związane ze zmianami w ilości rozpraszania strahlu. W niniejszej pracy analiza zmian strahlu będzie się koncentrować na plazmie obszaru sektora odwracania z jej ogólnie słabą intensywnością strahlu. Zmiany intensywności strahlu w szybkim wietrze słonecznym, (tj. plazmie pochodzącej z dziury koronalnej) (np. Hammond et al., 1996 [43]; Pagel et al., 2005b [75]; Louarn et al., 2009 [63]; Borovsky, 2016 [11]) gdzie intensywność strahlu pozostaje duża (por. Ilustracja 1), wskazując zawsze na magnetyczne połączenie z koroną, nie są badane, ponieważ te zmiany mogą nie dostarczać informacji o magnetycznych rozłączeniach (Przyszłe badanie zmian intensywności strahla w wietrze słonecznym z dziury koronalnej mogłoby jednak dostarczyć dodatkowych informacji o tym, jak interpretować zmiany strahla).
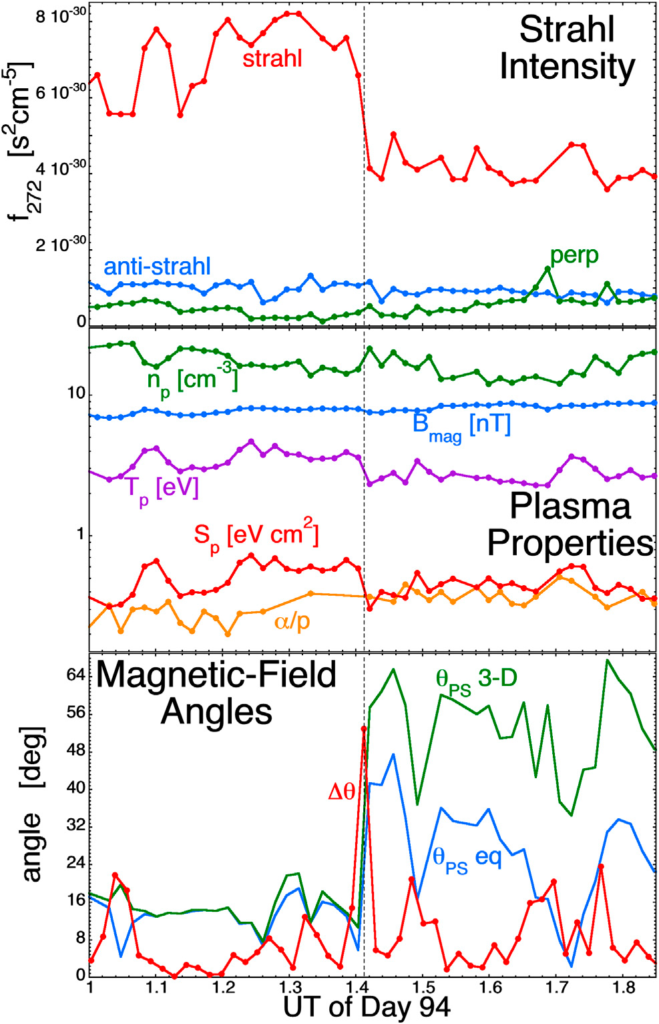
Na rysunkach 6 i 7 przedstawione są dwa przykłady zmian strahla, pochodzące z danych SWEPAM dla plazmy ACE o rozdzielczości 64 sekund i pola magnetycznego MAG (Smith et al., 1998 [92]) w L1. Pierwszą zmianą, na rysunku 6, był nagły spadek intensywności strahla w ACE o 1:24 UT 4 kwietnia (dzień 94) 2005 roku. W górnym panelu gęstość przestrzeni fazowej strahlu f272 o 272 eV jest wykreślona na czerwono, gęstość przestrzeni fazowej w przeciwnym kierunku (antystrahl) jest wykreślona na niebiesko, a gęstość przestrzeni fazowej elektronów o 272 eV prostopadłej do kierunku pola magnetycznego jest wykreślona na zielono. Spadek intensywności strahlu o około dwa współczynniki jest zaznaczony pionową czarną przerywaną linią. W środkowym panelu rysunku 6 znajduje się szereg parametrów plazmy: gęstość liczbowa protonów np (zielony), temperatura protonów Tp (fioletowy), entropia właściwa protonów Sp = Tp/np2/3 (czerwony), stosunek ilość/gęstość alfa do protonów α/p (pomarańczowy) oraz natężenie pola magnetycznego Bmag (niebieski). Zauważmy, że jednocześnie dla tego spadku natężenia strahla następuje spadek entropii właściwej protonów Sp i spadek temperatury protonów Tp. W dolnym panelu ilustracji 6 wykreślono kilka informacji o kierunku pola magnetycznego wiatru słonecznego: Δθ (czerwony) to zmiana kątowa kierunku pola magnetycznego co 64 s, θPS 3-D (zielony) to kąt między polem magnetycznym a kierunkiem spirali Parkera, a θPS eq (niebieski) to kąt między równikowym rzutem pola magnetycznego a kierunkiem Parkera-spirala. Duża wartość Δθ wskazuje na przejście przez silny arkusz prądowy: jak widać na wykresie Δθ, istnieje silny arkusz prądowy współwystępujący ze zmianą intensywności strahla (Patrz również: Borovsky (2020a) [14] dla statystycznego badania współwystąpień zmian intensywności strahla z silnymi arkuszami prądowymi). Zauważmy w dolnym panelu ilustracji 6, że w miarę zmniejszania się intensywności strahla, dwa obliczone kąty θPS wskazują, że pole magnetyczne wiatru słonecznego dokonuje przejścia z wyrównanego ze spiralą Parkera do niewyrównanego.
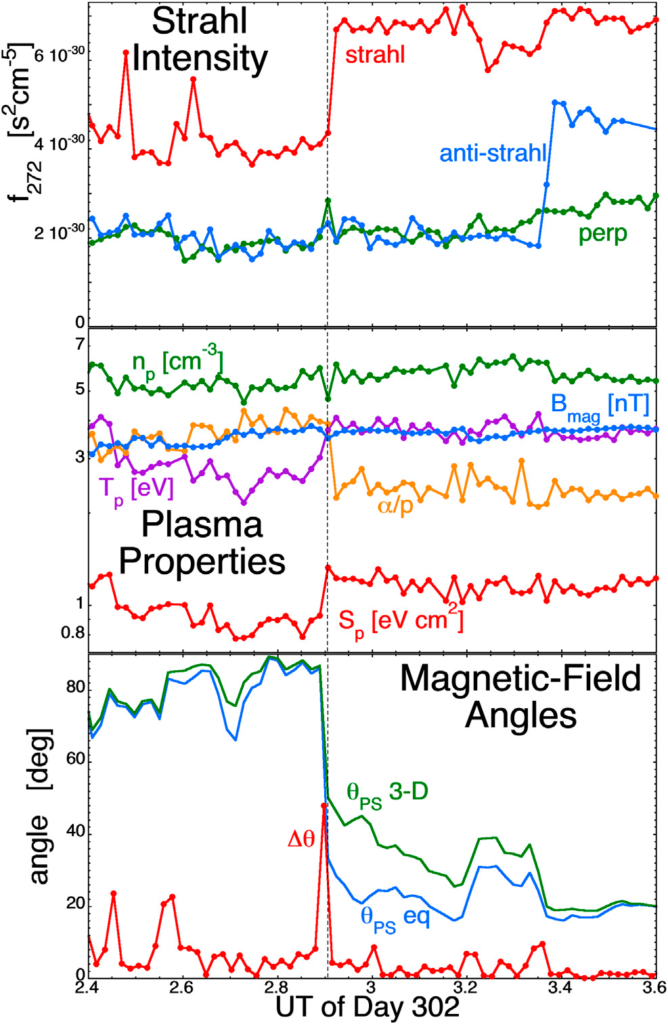
Ilustracja 7 jest podobna do ilustracji 6, gdzie wzrost intensywności strahla występuje w górnym panelu ilustracji 7 o 2:54 UT 29 października (dzień 302) 2005 roku. Wzrost ten zaznaczony jest pionową czarną przerywaną linią. W środkowym panelu ilustracji 7 wzrostowi intensywności strahla towarzyszy wzrost temperatury protonów Tp (fioletowy) i entropii właściwej protonów Sp (czerwony) oraz spadek stosunku liczby do gęstości alfa do protonów α/p (pomarańczowy). Dolny panel ilustracji 7 wskazuje na obecność silnego arkusza prądowego w miejscu zmiany strahla (czerwona krzywa Δθ), a pole magnetyczne wiatru słonecznego dokonuje przejścia z orientacji nie-parkerowskiej na bardziej parkerowską.
Dwie przyczyny rozpraszania strahlu elektronowego, które zostały dobrze zbadane w literaturze, to rozpraszanie Coulomba (Scudder and Olbert, 1979 [88]; Lemons and Feldman, 1983 [56]; Boldyrev et al., 2020 [8]) oraz rozpraszanie przez fale gwizdowe (Gary et al., 1975 [35]; Saito and Gary, 2007 [85]; Viñas et al., 2010 [103]). Różne mechanizmy mogą powodować rozpraszanie strahlu przy różnych energiach elektronów. Szybkość rozpraszania kątowego szybkich elektronów przez zderzenia kulombowskie SCoulomb jest proporcjonalna do gęstości liczbowej tła n w plazmie (por. (6.4.10) Krall i Trivelpiece (1973) [51] lub Sect. 3 z Tang et al., (2018) [94]), czyli SCoulomb ∝ n. Dla rozpraszania kątowego strahla przez turbulencję gwizdową o stałej amplitudzie, modelowanie wskazuje, że szybkość rozpraszania jest w przybliżeniu proporcjonalna do B3/n razy słaba potęga n/B2, co daje w przybliżeniu Swhistler ∝ B2/n1/2 (por. (B4) Steinackera i Millera (1992) [93], np. (8) Pierrarda et al., (2011) [77], lub Sect. 3 z Tang et al., (2018) [94]). Dla rozpraszania kątowego przez turbulencję kinetyczną fali Alfwena, por. (30) Boldyreva i Horiatesa. (2019) [9] daje to SkineticAlfven ∝ n.
Wykorzystując 64-sekundową rozdzielczość SWEPAM plazmy ACE oraz dane MAG o polu magnetycznym dla roku 2005, przeanalizowano 528 silnych zmian w intensywności strahlu elektronów w 1 AU: 282 z tych 528 zmian strahla wystąpiło, gdy plazma wiatru słonecznego została sklasyfikowana jako plazma regionu sektora zawracania, a 246 zmian wystąpiło w wietrze o vsw < 460 km/s, który został sklasyfikowany jako plazma wyrzutowa lub pochodząca z pasa wstęgowego. Ta lista skoków zebranych w 2005 roku nie jest w żadnym wypadku wyczerpująca. Zebrano tylko 528 skoków z powodu ograniczeń 1) że skoki muszą wystąpić w plazmie regionu sektora zawracania lub w powolnym wietrze otaczającym plazmę sektora zawracania, 2) skok musi reprezentować wzrost lub spadek intensywności strahla, który jest zmianą w intensywności o 50% lub więcej w skali czasowej 1 lub dwóch punktów danych, 3) że musi istnieć wyraźne utrzymywanie się intensywności strahla przez kilka minut zarówno przed, jak i po skoku, oraz 4) pomiary strahl i plazmy muszą być wolne od pobliskich strzępów danych. To ostatnie ograniczenie było najsilniejsze, ponieważ potwierdzone pomiary protonowo-plazmowe ACE SWEPAM są zwykle nieobecne, gdy prędkość wiatru słonecznego jest bardzo niska, jak to ma miejsce w plazmie regionu sektora zawracania. Analiza statystyczna 528 zmian intensywności strahla z roku 2005 jest podsumowana w Tabeli 1 i przedstawiona graficznie na Ilustracji 8.
Tabela 1: Statystyczny związek zmian intensywności strahla ze zmianami innych parametrów plazmy w roku 2005.
| Wielkość | Zbiór skoków strahla | Zmiana przeciwna do I272 (%) | Brak zaobserwowanej zmiany (%) | Zmiana zgodna z kierunkiem I272 (%) | Ułamek czasu obserwacji zmiany (%) | Stosunek zgodnych do przeciwnych |
| Sp | Wsz. 528 | 10,6 | 42,0 | 47,4 | 58,0 | 4,47/1 |
| Sektor zawr. | 11,0 | 40,4 | 48,6 | 59,6 | 4,42/1 | |
| Poz. pow. | 10,2 | 43,9 | 45,9 | 56,1 | 4,52/1 | |
| np | Wsz. 528 | 31,3 | 57,0 | 11,7 | 43,0 | 1/2,66 |
| Zektor zawr. | 34,8 | 53,6 | 11,7 | 46,6 | 1/2,97 | |
| Poz. pow. | 27,2 | 61,0 | 11,8 | 39,0 | 1/2,30 | |
| Tp | Wsz. 528 | 13,4 | 43,6 | 43,0 | 56,4 | 3,20/1 |
| Sektor zawr. | 12,1 | 46,5 | 41,5 | 53,6 | 3,44/1 | |
| Poz. pow. | 15,0 | 40,2 | 44,7 | 59,7 | 2,97/1 | |
| Bmag | Wsz. 528 | 8,9 | 64,4 | 26,7 | 35,6 | 3,00/1 |
| Sektor zawr. | 12,4 | 55,7 | 31,9 | 44,3 | 2,57/1 | |
| Poz. pow. | 4,9 | 74,4 | 20,7 | 25,6 | 4,25/1 | |
| α/p | Wsz. 528 | 16,4 | 70,8 | 12,9 | 29,3 | 1/1,27 |
| Sektor zawr. | 19,0 | 67,7 | 13,3 | 32,3 | 1/1,43 | |
| Poz. pow. | 13,2 | 74,4 | 12,4 | 25,6 | 1/1,07 | |
| θPS | Wsz. 528 | 24,1 | 69,5 | 6,4 | 30,5 | 1/3,73 |
| Sektor zawr. | 22,0 | 69,2 | 8,9 | 30,9 | 1/2,48 | |
| Poz. pow. | 26,4 | 69,9 | 3,7 | 30,1 | 1/7,22 |
Dla silnych zmian intensywności strahlu elektronowego zwracano uwagę na znak jednoczesnych zmian natężenia pola magnetycznego Bmag, gęstości liczbowej protonów np, temperatury protonów Tp, entropii właściwej protonów Sp = Tp/np2/3, stosunku gęstości liczbowej alfa do protonów α/p oraz zmiany kąta θPS pomiędzy orientacją pola magnetycznego a kierunkiem spirali Parkera. Zmiana każdego z parametrów była rejestrowana tylko 1) jeśli parametr wykazywał jednoczesne przesunięcie (skok) w swojej wielkości oraz 2) jeśli zmiana przesunięcia była większa niż poziomy fluktuacji tego parametru przed i po zmianie. Zmiana w θPS była rejestrowana tylko wtedy, gdy kierunek pola silnie zmienił się z orientacji, która zdecydowanie byłaby sklasyfikowana jako zgodna ze spiralą Parkera do orientacji zdecydowanie niezgodnej (zmiana pozytywna) lub odwrotnie (zmiana negatywna) (są to zwykle zmiany kątowe o więcej niż 45°). Dla wszystkich 528 zmian intensywności strahla, statystyki jednoczesnych zmian tych innych wielkości zebrano w Tabeli 1. Pierwsze trzy kolumny danych w Tabeli 1 zawierają ułamek czasu, w którym zmiana była w tym samym kierunku co zmiana intensywności strahla, (tj. obie jednocześnie wzrastające lub obie jednocześnie malejące), ułamek czasu, w którym zmiany były w przeciwnych kierunkach, oraz ułamek czasu, w którym nastąpiła zmiana intensywności strahla, ale nie było zmiany w innej wielkości, która była większa niż poziom szumu w pomiarach. Każdy zestaw trzech wierszy w Tabeli 1 przedstawia statystyki dla wszystkich 528 zmian strahla, statystyki dla 282 zmian strahla w plazmie sektora zawracania oraz statystyki dla 246 zmian strahla w innych typach powolnego wiatru słonecznego. Dla każdej zmiennej zauważmy, że liczby statystyczne w Tabeli 1 są podobne dla każdego z trzech rzędów: podobieństwo w statystyce 282 zmian strahla plazmy w sektorze zawracania i 246 innych zmian strahla wskazuje, że wyniki statystyczne są solidne, ponieważ podobne wartości są uzyskiwane dla dwóch niezależnych zestawów zdarzeń. Dla wierszy „Wsz. 528”, pierwsze trzy kolumny są graficznie przedstawione na Ilustracji 8, gdzie kolor zielony odpowiada zmianom tego samego znaku (korelacja), czerwony zmianom przeciwnego znaku (antykorelacja), a szary reprezentuje brak zaobserwowanych wyraźnych zmian. Druga od końca kolumna Tabeli 1 to ułamek zdarzeń związanych ze zmianą strahla, w których zaobserwowano zmiany w innej interesującej nas wielkości. W Tabeli 1 najsilniejsze powiązania ze zmianami intensywności strahla występują dla zmiennych Sp i Tp, przy czym 58% i 56% zmian strahla towarzyszyło zmianom odpowiednio tych dwóch zmiennych. Zauważmy, że tylko 35,6% zmian strahla towarzyszą zmiany Bmag; ponadto, ponieważ pomiary Bmag w 64-sekundowym zbiorze danych ACE mają bardzo niski poziom szumów, łatwiej jest znaleźć pojawiającą się zmianę Bmag, niż w przypadku innych zmiennych plazmy. Nadal tylko 35,6% zmian intensywności strahla miało zmiany Bmag: stąd związek zmian Bmag ze zmianami strahla jest znacznie słabszy niż związek innych zmiennych plazmy. Zauważmy również, że zmiany kąta θPS pomiędzy orientacją pola magnetycznego a kierunkiem spirali Parkera są liczone jako niezerowe tylko wtedy, gdy zmiana kąta jest bardzo silna, (np. przejście od bardzo niskiego kąta do większego niż 45° lub odwrotnie); stąd w rzeczywistości związek zmian intensywności strahla z przejściem pomiędzy zgodnością a niezgodnością ze spiralą Parkera jest prawdopodobnie większy niż ∼31° odnotowane w Tabeli 1.
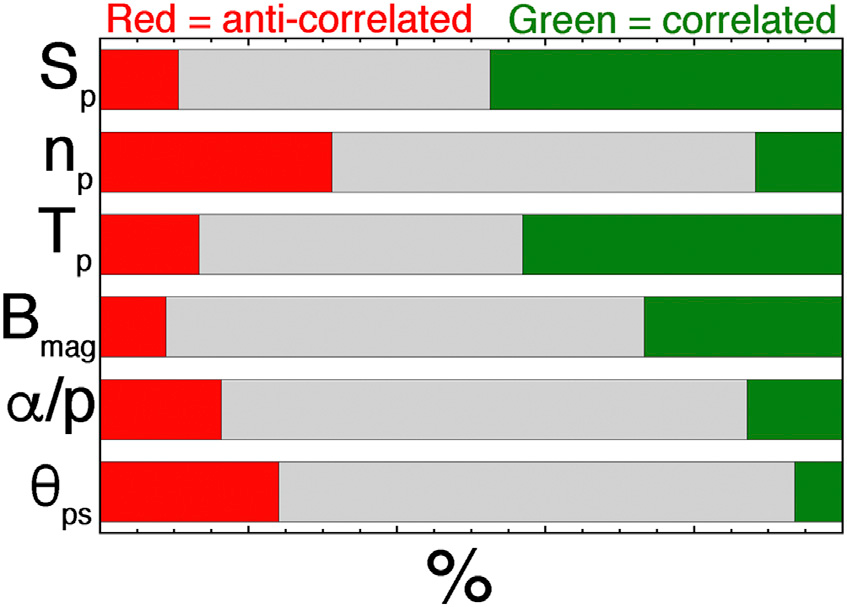
Ostatnia kolumna Tabeli 1 zawiera stosunek liczby zmian, które były tego samego znaku co zmiana intensywności strahla do liczby zmian, które były przeciwnego znaku. Zmiany intensywności strahla były dodatnio skorelowane ze zmianami Sp, Tp , i Bmag, natomiast były przeciwnie korelowane ze zmianami np, α/p, i θPS. Najsilniejsze powiązania ze zmianą strahla dotyczyły Sp i Tp. Dla wszystkich 528 zmian strahla, zmiany Sp, które były tego samego znaku co zmiany intensywności strahla, były 4,47 razy bardziej prawdopodobne do znalezienia niż zmiany Sp, które były przeciwnego znaku niż zmiana strahla. Stąd zmiany tego samego znaku są zdecydowanie preferowane. Dla Tp ten stosunek w Tabeli 1 wynosi 3,20 do 1. Dla zmian Bmag było 3,0 razy większe prawdopodobieństwo, że będą tego samego znaku co zmiana natężenia strahla, niż przeciwnego znaku, ale zmiany Bmag były obserwowane tylko dla 35,6% zmian strahla.
Ogólnie rzecz biorąc, zmiany stosunku liczby alfa do liczby protonów α/p są słabo związane ze zmianami intensywności strahla, przy czym tylko 29,3% zmian strahla miało wyraźnie rozpoznane zmiany α/p, a liczba zmian α/p, które były tego samego znaku co zmiany strahla, była mniej więcej równa liczbie zmian α/p, które były przeciwnego znaku.
W przypadku zmian intensywności strahla spowodowanych zmianami w ilości rozpraszania gwizdowo-turbulencyjnego (przy czym siła rozpraszania przebiega w przybliżeniu jako Swhistler ∝ B2/ n1/2), można by oczekiwać, że intensywność strahlu wzrośnie, gdy Bmag maleje i/lub gdy np wzrasta: jednak Tabela 1 wskazuje, że występuje odwrotna tendencja zarówno dla Bmag, jak i np.
W przypadku zmian intensywności strahla spowodowanych zmianami ilości rozpraszania kulombowskiego lub ilości rozpraszania turbulencji kinetycznych Alfvéna (z SCoulomb ∝ n i z SkineticAlfven ∝ n), należałoby oczekiwać, że intensywność strahla będzie wzrastać, gdy gęstość liczbowa np będzie maleć, co widać w asocjacji zmian strahla z np w Tabeli 1. Jednak zmiany np są widoczne tylko dla 43,0% zmian intensywności strahla, a zmiany w Tp i Sp są silniejsze, niż zmiany w np. Tabela 1 daje słabe poparcie dla rozpraszania strahla przez zderzenia Coulomba lub przez kinetyczne fale Alfvéna.
W zestawieniach, zawartych w Tabeli 1, istnieje umiarkowane poparcie dla tezy, że transfery z plazmy zorientowanej na spiralę Parkera do plazmy niezorientowanej skutkują zmniejszeniem intensywności strahli oraz że transfery z plazmy niezorientowanej na Parkera do plazmy zorientowanej na Parkera skutkują zwiększeniem intensywności strahli.
Zauważmy, że poprzez Tabelę 1 są badane związki między zmianami intensywności strahlu w 1 AU a zmianami własności plazmy w 1 AU oraz dokonuje się ich interpretacji; jednakże zmiany w poprzek tych samych granic intensywności strahlu bliżej Słońca niż 1 AU mogą mieć inny charakter niż zmiany obserwowane w 1 AU.
Tabela 2: Współczynniki korelacji liniowej Pearsona dla wszystkich danych wiatru słonecznego pomiędzy uśrednionymi co godzinę parametrami tegoż wiatru, w tym natężeniem strahla I272 = Log10 (f272).
| I272 | Log (Sp) | Log (Tp) | Log (np) | vsw | Log (Bmag) | α/p | δBvec | Log (C6+/C4+) | Log (C6+/C5+) | Log (O7+/O6+) | Log (Fe/O) | θPS rów-nikowe | θPS 3-D | |
| I272 | 1 | 0.22 | 0.33 | 0.11 | 0.16 | 0.63 | 0.28 | 0.34 | 0.09 | 0.04 | 0.10 | 0.08 | −0.16 | −0.15 |
| Log (Sp) | 0.22 | 1 | 0.91 | −0.64 | 0.77 | 0.15 | 0.30 | 0.26 | −0.40 | −0.32 | −0.55 | −0.35 | −0.13 | −0.18 |
| Log (Tp) | 0.33 | 0.91 | 1 | −0.26 | 0.70 | 0.31 | 0.30 | 0.46 | −0.37 | −0.32 | −0.52 | −0.34 | −0.13 | −0.15 |
| Log (np) | 0.11 | −0.64 | −0.26 | 1 | −0.47 | 0.22 | −0.16 | 0.25 | 0.25 | 0.16 | 0.31 | 0.17 | 0.07 | 0.12 |
| vsw | 0.16 | 0.77 | 0.70 | −0.47 | 1 | 0.20 | 0.27 | 0.30 | −0.50 | −0.50 | −0.48 | −0.33 | −0.04 | −0.07 |
| Log (Bmag) | 0.63 | 0.15 | 0.31 | 0.22 | 0.20 | 1 | 0.32 | 0.51 | 0.12 | 0.05 | 0.19 | 0.13 | −0.10 | −0.05 |
| α/p | 0.28 | 0.30 | 0.30 | −0.16 | 0.27 | 0.32 | 1 | 0.22 | −0.09 | −0.13 | 0.06 | −0.02 | −0.05 | −0.06 |
| δBvec | 0.34 | 0.26 | 0.46 | 0.25 | 0.30 | 0.51 | 0.22 | 1 | −0.06 | −0.08 | −0.10 | −0.05 | −0.04 | 0.01 |
| Log (C6+/C4+) | 0.09 | −0.40 | −0.37 | 0.25 | −0.49 | 0.16 | −0.09 | −−0.06 | 1 | 0.93 | 0.79 | 0.25 | 0.06 | 0.09 |
| Log (C6+/C5+) | 0.04 | −0.32 | −0.32 | 0.16 | −0.50 | 0.05 | −−0.13 | −0.08 | 0.93 | 1 | 0.69 | 0.23 | 0.06 | 0.08 |
| Log (O7+/O6+) | 0.10 | −−0.55 | −0.52 | 0.31 | −0.48 | 0.19 | 0.06 | −0.10 | 0.79 | 0.69 | 1 | 0.42 | 0.11 | 0.148 |
| Log (Fe/O) | 0.08 | −0.35 | −0.34 | 0.17 | −0.33 | 0.13 | −0.02 | −0.05 | 0.25 | 0.23 | 0.42 | 1 | 0.03 | 0.06 |
| θPS rów-nikowe | −0.16 | −0.13 | −0.13 | 0.07 | −0.04 | −0.10 | −0.05 | −0.04 | 0.06 | 0.06 | 0.11 | 0.03 | 1 | 0.86 |
| θPS 3-D | −0.15 | −0.18 | −0.15 | 0.12 | −0.07 | −0.05 | −0.06 | 0.01 | 0.09 | 0.08 | 0.15 | 0.06 | 0.86 | 1 |
Dalszych informacji o intensywności strahla dostarczają tabele 2 i 3, które zawierają współczynniki korelacji liniowej Pearsona między średnimi godzinowymi logarytmami intensywności strahla I272 Log10 (f272) koło Ziemi a średnimi godzinowymi różnych parametrów wiatru słonecznego tamże. Korelacje I272 z parametrami wiatru słonecznego, wymienionymi w tabelach 2 i 3 zostały również przedstawione graficznie na rysunku 9. Tabele 2 i 3 dostarczają również informacji o wzajemnych korelacjach pomiędzy zmiennymi wiatru słonecznego. Należy zwrócić uwagę, że w korelacjach zastosowano logarytmy niektórych zmiennych: dla niektórych zmiennych (np. np, Sp, Tp i Bmag) pozwala to na uniknięcie silnego wpływu na współczynniki korelacji wartości odstających, a inne zmienne są współczynnikami (np. C6+/C4+, C6+/C5+, O7+/O6+ i Fe/O) i użycie logarytmu ze stosunku daje większą wagę w korelacjach do bardzo małych wartości tego stosunku; innymi słowy, logarytmy tych zmiennych są bliższe rozkładowi Gaussa. Tabela 2 dotyczy wszystkich danych o wietrze słonecznym, a Tabela 3 dotyczy okresów, w których wiatr słoneczny został zakwalifikowany jako plazma sektora zawracania. Informacje o korelacji strahla z Tabeli 2 i 3 są powiązane, ale nie dokładnie takie same jak informacje z Tabeli 1. Informacja z Tabeli 1 odpowiada na pytanie: czy gdy zmienia się intensywność strahla, to dana wielkość plazmy X dokonuje zmiany w tym samym kierunku? Informacje z Tabeli 2 i 3 odpowiadają na pytanie: jak dobrze można przewidzieć wartość I272, jeśli znana jest wartość wielkości plazmowej X? Tabele 2 i 3 odpowiadają również na pytanie: czy duże wartości X są związane z dużymi wartościami I272 i czy małe wartości X są związane z małymi wartościami I272? Tabele 2 i 3 wykorzystują uśrednione godzinowo wartości elektronów strahl z ACE SWEPAM, uśrednione godzinowo wartości parametrów plazmy i pola wiatru słoneczego z OMNI2 oraz uśrednione godzinowo pomiary ciężkich jonów z ACE SWICS (Gloeckler et al., 1998 [38]) (wersja „1.1” zestawu danych SWICS). Wykorzystano wartości strahla w latach 1998-2013. W tabelach 2 i 3 δBvec jest amplitudą skuteczną fluktuacji wektora pola magnetycznego w każdej godzinie danych, a δBvec/Bmag jest amplitudą kąta odchylenia (w radianach) wektora pola magnetycznego wiatru słonecznego w każdej godzinie. W tabelach 2 i 3 kąt θPS pomiędzy kierunkiem pola magnetycznego a kierunkiem spirali Parkera jest obliczany na dwa sposoby: 1) kierunek równikowej projekcji pola magnetycznego z kierunku spirali Parkera oraz 2) pełny trójwymiarowy kierunek pola względem kierunku spirali Parkera. Ten ostatni obejmuje składową Bz (lub Bn) pola. Dla współczynników korelacji nie ma to znaczenia, ale logarytmy są logarytmami o podstawie 10. Szum statystyczny we współczynnikach korelacji z tabel 2 i 3 jest bardzo mały. Dla N punktów skorelowanych poziom szumu statystycznego na współczynniku korelacji wynosi 2/(N+1)1/2 (Beyer, 1966 [6]; Bendat i Piersol, 1971 [4]). W Tabeli 2 jest N = 127 130 punktów danych dla I272, dających poziom szumu statystycznego ±0,006 dla współczynników korelacji, a w Tabeli 3 jest N = 25 569 punktów danych dla I272, dających poziom szumu statystycznego ±0,013 dla współczynników korelacji.
Tabela 3: Współczynniki korelacji liniowej Pearsona pomiędzy godzinowo uśrednianymi parametrami wiatru słonecznego, w tym intensywnością strahl I272 Log10 (f272 ).
| I272 | Log (Sp) | Log (Tp) | Log (np) | vsw | Log (Bmag) | α/p | δBvec | Log (C6+/C4+) | Log (C6+/C5+) | Log (O7+/O6+) | Log (Fe/O) | θPS równ. | θPS 3-D | |
| I272 | 1 | 0.11 | 0.29 | 0.24 | 0.22 | 0.51 | 0.25 | 0.31 | 0.06 | −0.02 | 0.33 | 0.13 | −0.09 | −0.07 |
| Log (Sp) | 0.11 | 1 | 0.74 | −0.35 | 0.31 | 0.06 | 0.16 | 0.12 | 0.13 | 0.22 | −0.25 | −0.02 | 0.00 | −0.01 |
| Log (Tp) | 0.29 | 0.74 | 1 | 0.37 | 0.36 | 0.37 | 0.20 | 0.47 | 0.05 | 0.07 | −0.07 | −0.04 | −0.01 | 0.01 |
| Log (np) | 0.24 | −0.35 | 0.37 | 1 | 0.07 | 0.43 | 0.06 | 0.48 | −0.12 | −0.21 | 0.25 | −0.01 | −0.02 | 0.03 |
| vsw | 0.22 | 0.31 | 0.36 | 0.07 | 1 | 0.18 | 0.29 | 0.21 | −0.18 | −0.28 | 0.21 | −0.09 | 0.09 | 0.10 |
| Log (Bmag) | 0.51 | 0.06 | 0.37 | 0.43 | 0.18 | 1 | 0.26 | 0.50 | −0.06 | −−0.13 | 0.23 | 0.14 | −0.07 | −−0.03 |
| α/p | 0.25 | 0.16 | 0.47 | 0.06 | 0.29 | 0.26 | 1 | 1 | −0.25 | −−0.38 | 0.46 | 0.11 | 0.04 | 0.04 |
| δBvec | 0.31 | 0.12 | 0.20 | 0.48 | 0.21 | 0.50 | 0.15 | 0.15 | −0.05 | −0.07 | 0.06 | 0.08 | −0.02 | 0.05 |
| Log (C6+/C4+) | 0.06 | 0.13 | 0.05 | −0.12 | −0.18 | −0.06 | −0.25 | −0.05 | 1 | 0.89 | 0.24 | −0.10 | −0.06 | −0.06 |
| Log (C6+/5+C ) | −0.02 | 0.22 | 0.07 | −0.21 | −0.28 | −0.13 | −0.38 | −0.07 | 0.89 | 1 | 0.01 | −0.04 | −0.05 | −0.06 |
| Log (O7+/O6+) | 0.33 | −−0.25 | −0.07 | 0.25 | 0.21 | 0.23 | 0.46 | 0.06 | 0.24 | 0.01 | 1 | 0.14 | 0.00 | 0.01 |
| Log (Fe/O) | 0.13 | −0.02 | −0.04 | −0.01 | −0.09 | 0.14 | 0.11 | 0.08 | −0.10 | −0.04 | 0.14 | 1 | −0.00 | 0.00 |
| θPS równ. | −0.09 | 0.00 | −0.01 | −0.02 | 0.09 | −0.07 | 0.04 | −0.02 | −0.06 | −0.05 | 0.00 | −0.00 | 1 | 0.85 |
| θPS 3-D | −0.07 | −0.01 | 0.01 | 0.03 | 0.10 | −0.03 | 0.04 | 0.05 | −0.06 | −0.06 | 0.01 | 0.00 | 0.85 | 1 |
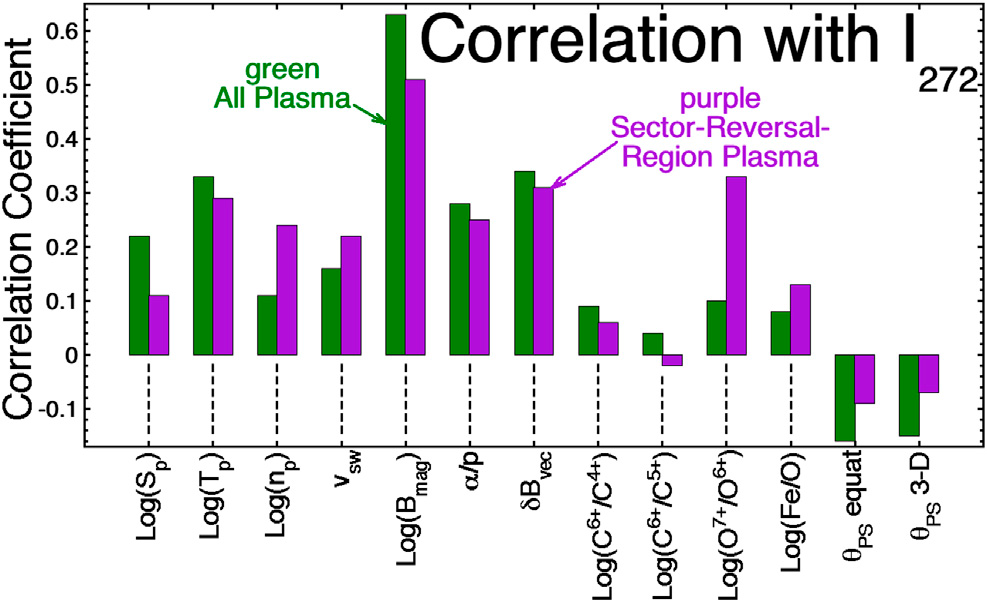
Pomiędzy Tabelą 2, dotyczącą całego wiatru słonecznego, a Tabelą 3, dotyczącą plazmy sektora zawracania, występują często znaczne różnice we współczynnikach korelacji pomiędzy zmiennymi dotyczącymi wiatru słonecznego. W korelacjach ogólnosłonecznych z Tabeli 2, wiele korelacji i antykorelacji jest tworzonych 1) przez wielkoskalowe kompresje i dekompresje plazmy z powodu dużych zmian prędkości wiatru słonecznego oraz 2) przez napędzane rotacją słoneczną sekwencyjne przełączanie pomiędzy typami plazmy, które mają systematyczne różnice w swoich parametrach (por. Borovsky, 2018 [13]). W korelacjach plazmy sektora zawracania z Tabeli 3 nie działa żaden z tych dwóch mechanizmów, ponieważ 1) zakres prędkości plazmy sektora zawracania jest dość ograniczony oraz 2) występuje tylko jeden typ plazmy wiatru słonecznego. Ogólnie rzecz biorąc, ponieważ dane użyte w Tabeli 3 są podzbiorem danych użytych w Tabeli 2, a ten podzbiór został wybrany poprzez ograniczenie zakresu niektórych parametrów wiatru słonecznego, oczekuje się, że współczynniki korelacji w Tabeli 3 będą mniejszej wielkości niż współczynniki w Tabeli 2. Zauważalne korelacje z I272, które są w rzeczywistości wyższe w Tabeli 3 dla plazmy sektora zawracania niż w Tabeli 2 dla całego wiatru, to korelacje I272 z log (np), z vsw, oraz z log (O7+/O6+) (patrz także Ilustracja 9).
W Tabeli 3 najsilniejsze korelacje I272 występują z Log (Bmag). Jeśli jest zachowany wyrównany do pola strumień elektronów strahla, to oczekuje się dodatniej korelacji pomiędzy I272 a Bmag, (np. w Tabelach 1-3 i na Ilustracji 9); widać to bardzo wyraźnie w kompresjach CIR i dekompresjach ciągnionej z tyłu krawędzi, gdzie linie pola magnetycznego są ściśnięte razem lub rozszerzone, a wzór intensywności strahla podąża za wzorem siły pola magnetycznego (Crooker et al., 2010 [25]; Borovsky, 2016 [11]). Kolejne najsilniejsze korelacje I272 w Tabeli 3 są z Log (07+/O6+), δBvec, oraz Log (Tp) (przy czym δBvec jest silnie skorelowany z Bmag). Porównując korelacje I272 z Tabeli 3 z wynikami zmian strahla z Tabeli 1, korelacje z Tabeli 3 wspierają pozytywne korelacje zmian intensywności strahlów ze zmianami w Sp, Tp i Bmag, a korelacje z Tabeli 3 wspierają antykorelacje zmian intensywności strahlów ze zmianami w θPS. Dodatnie korelacje I272 z np i α/p w Tabeli 3 są przeciwne do wyników z tabeli 1, mówiących o antykorelacjach zmian intensywności strahlu ze zmianami np i α/p. Oczywiście, wykorzystując korelacje z Tabeli 3 jako wsparcie lub brak wsparcia dla trendów zmian strahlu z Tabeli 1, należy zdawać sobie sprawę, że czynniki napędzające wielkoskalową korelację z intensywnością strahla (Tabela 3) mogą nie być tymi samymi czynnikami, które napędzają nagłe ∼50% zmiany intensywności strahla z Tabeli 1.
Dyskusja: interpretacja zmian intensywności strahla, ocena połączenia Słońce-Ziemia i przyszłość
Mając świadomość, że na elektrony o różnych energiach mogą działać w strahlu różne mechanizmy, badając zmiany intensywności strahla 272 eV w plazmie sektora zawracania i innych powolnych wiatrów słonecznych (Tabela 1) stwierdzono, że wzrosty lub spadki intensywności strahlu są dodatnio skorelowane ze wzrostami lub spadkami Sp, Tp i Bmag oraz że wzrosty lub spadki intensywności strahlu są antyskorelowane z np, θPS i wzrostami lub spadkami α/p. W odniesieniu do antykorelacji Bmag i α/p należy zauważyć, że 1) większość (64,4%) zmian intensywności strahlu nie wykazuje zmian Bmag oraz 2) związek zmian α/p ze zmianami strahla jest słaby.
Wyniki analizy zmian strahlu 272 eV są niezgodne z modelem stałej amplitudy dla gwizdowo-turbulencyjnego rozpraszania strahlu jako przyczyny zmian jego intensywności; dla rozpraszania gwizdowego zmiany intensywności strahlu powinny być skorelowane ze zmianami np i antyskorelowane ze zmianami Bmag, a obserwuje się odwrotne korelacje. Analiza zmian strahlu 272 eV słabo wspiera rozpraszanie Coulomba i/lub rozpraszanie kinetyczno-falowe Alfvéna jako przyczynę tychże zmian; wsparcie jest tylko słabe, ponieważ oczekiwana antykorelacja zmian intensywności strahlu z np nie jest najsilniejszym związkiem ze zmianami strahlu (Dalej, korelacje wiatru słonecznego z Tabeli 3 pokazują, że intensywność strahlu dodatnio koreluje z np). Najsilniejszy związek zmian intensywności strahlu dotyczy zmian Tp i Sp, które nie są zaangażowane w scenariusze rozpraszania Coulomba, rozpraszania gwizdowego, czy rozpraszania kinetyczno-falowego Alfvéna.
Najsilniejszy związek ze zmianami intensywności strahli wykazują dodatnie korelacje ze zmianami Sp i Tp (Tabela 1). Czynniki rządzące wartościami Sp i Tp w wietrze słonecznym nie są dobrze poznane. Wartość protonowej entropii właściwej Sp wiatru słonecznego w 1 AU jest silnym wskaźnikiem typu plazmy (por. rysunek 3 u Xu i Borovsky’ego (2015) [108]). Wyłączając plazmę wyrzutową, temperatura protonów Tp wiatru słonecznego w 1 AU jest silnie związana z vsw (por. rysunek 1 Lopeza i Freemana (1986) [62], rysunek 12 Borovsky’ego i Steinberga (2006) [17], rysunki. 4 i 5 z Elliott et al., (2012) [30]). Entropia właściwa protonu Sp jest również silnie dodatnio skorelowana z vsw (por. tabele 2 i 3).
W wolniejszym wietrze słonecznym (takim jak plazma regionu sektora zawracania) wiadomo, że obserwowana prędkość wiatru słonecznego vsw systematycznie rośnie wraz z odległością od Słońca powyżej 0.3 AU (Schwenn et al., 1981 [87]; Arya i Freeman, 1991 [2]): może to być wynikiem napędzanego gorącymi elektronami międzyplanetarnego ambipolarnego potencjału elektrycznego, przyspieszającego protony wiatru słonecznego od Słońca (Jockers, 1970 [46]; Lemaire, 2010 [55]; Pierrard, 2012 [78]; Borovsky i Gary, 2014 [16]). Dane zmian strahlu (Tabela 1) i korelacji strahla (Tabela 3) wskazują, że słabsze strahle plazmy regionu sektora zawracania są związane ze słabszymi temperaturami protonów i słabszymi entropiami właściwymi protonów, a dane korelacyjne wskazują, że słabsze strahle są związane z wolniejszym wiatrem słonecznym w 1 AU. Te korelacje mogą być zgodne ze słabszym, napędzanym elektronami, międzyplanetarnym polem elektrycznym z powodu słabego połączenia magnetycznego z koroną lub z połączeniami, które produkują słaby strahl. Zauważmy jednak, że współczynniki korelacji w Tabeli 3 są słabe, co wskazuje, że intensywność strahlu nie jest dominującym czynnikiem wpływającym na wartości protonów.
W zestawie danych dotyczących wiatru słonecznego (Tabela 2), Sp jest silnie antyskorelowane ze stosunkiem stanów ładunkowych ciężkich jonów C6+/C4+, C6+/C5+ i O7+/O6+, ale w plazmie z regionu sektora zawracania (Tabela 3) korelacje te komplikują się, gdyż Sp jest antyskorelowane z C6+/C4+ i C6+/C5+, a dodatnio skorelowane z O7+ /O6+. Relacja stanów ładunkowych tlenu do stanów ładunkowych węgla różni się w plazmie sektora zawracania (i wyrzutowej) od ich relacji w plazmie pochodzącej z dziury koronalnej i plazmie pochodzącej z pasa wstęgowego (por. rysunki. 10 i 12 Xu i Borovsky’ego (2015) [108] oraz rysunek 1 Zhao et al., (2016) [110]); Xu i Borovsky (2015) [108] spekulowali, że ta relacja stanów ładunkowych węgiel-tlen jest wskaźnikiem impulsywnej vs. stałej emisji plazmy z korony, przy czym plazma z sektora zawracania jest momentami impulsywna.
Analiza zmian strahlu pokazuje również antykorelację pomiędzy zmianami intensywności strahlu a zmianami kąta θPS pola magnetycznego od kierunku spirali Parkera: jest to zgodne z silniejszym strahlem w plazmie spirali Parkera (emitowanej w sposób ciągły z otwartym strumieniem magnetycznym z korony) w porównaniu z plazmą spoza spirali Parkera (emitowanej impulsywnie, być może z rozłączeniami magnetycznymi). Mogą jednak istnieć różnice w długości pola magnetycznego pomiędzy polami spirali Parkera a polami spoza niej, które również mogą odgrywać rolę w intensywności strahla w odległości 1-AU.
Badając nagłe zmiany intensywności strahlu elektronów w 1 AU, którym towarzyszą nagłe zmiany kierunku pola magnetycznego, Gosling et al., (2004A,B) [39] spekulowali, że nagłe zmiany intensywności strahla są przejawem nagłych zmian w odwzorowaniu pola magnetycznego wiatru słonecznego z powrotem do korony. W statystyce zmian strahlu w Tabeli 1, silne zmiany kierunku pola ze zgodnego ze spiralą Parker do niezgodnego mogą odpowiadać za ∼25% zmian strahla. Ta zmiana w połączeniu z koroną jest również wspierana przez zmiany właściwości plazmy, które towarzyszą zmianom intensywności strahlu (Tabela 1) (Jednakże w Tabeli 1 najsłabszy związek zmiany strahla jest z α/p, które powinno zmieniać się wraz z magnetycznym połączeniem z koroną). Ponadto, ten obraz zmiany w połączeniu magnetycznym jest wspierany przez symulacje MHD powyżej korony u Burkholder’a et al., (2019) [19], gdzie arkusze prądowe w plazmie reprezentują topologiczne zmiany w mapowaniu magnetycznym z powrotem do fotosfery.
Plazma sektora odwracania w 1 AU charakteryzuje się szerokim zakresem niskich intensywności strahla oraz nagłymi zmianami w jego intensywności. Analiza zmian intensywności strahla w 1 AU sugeruje, że zmiany te są spowodowane zmianami w połączeniu magnetycznym z koroną. Kiedy intensywność strahla zmienia się na niskie wartości, pojawia się pytanie: Które niskie wartości reprezentują brak połączenia magnetycznego ze Słońcem, a które są spowodowane czymś innym? Powiązane pytanie brzmi: Dlaczego intensywność strahla jest tak niska, jeśli nadal jest on magnetycznie połączony z koroną?
Analiza intensywności strahli podczas impulsowych zdarzeń SEE została wykorzystana do przetestowania pomysłu, że obecność lub brak strahli może być użyta do oceny magnetycznego połączenia ze Słońcem. Test ten był oparty na założeniu, że zdarzenia SEE na Ziemi mogą wystąpić tylko wtedy, gdy Ziemia jest dobrze połączona magnetycznie ze Słońcem. Test SEE nie był pomocny w dokonaniu tej oceny: zdarzenia SEE występują podczas maksimum słonecznego, a analiza wykazała, że strahl jest podczas maksimum prawie zawsze silny.
Aby ocenić jakość połączenia magnetycznego pomiędzy wiatrem słonecznym w pobliżu Ziemi a Słońcem, użyto trzech narzędzi: 1) intensywność strahla, 2) orientację θPS pola magnetycznego wiatru słonecznego względem kierunku spirali Parkera, oraz 3) typ plazmy wiatru słonecznego. Użycie intensywności strahla jest najbardziej obiecujące, choć pozostają pytania, czy gdy intensywność strahlu w 1 AU jest niska, to 1) czy pole magnetyczne jest odłączone od Słońca, 2) czy pole magnetyczne jest podłączone do regionu korony, który produkuje słaby strahl, lub 3) czy strahl został zniszczony między Słońcem a 1 AU? Użycie orientacji pola magnetycznego θPS, wraz z obserwacją intensywności strahlu, dostarcza więcej wskazówek, czy pole magnetyczne jest odłączone od Słońca, czy nie. Użycie kategoryzacji plazmy „plazma sektora zawracania” (przy czym kategoryzacja dokonana jest przy użyciu jedynie pomiarów protonów i natężenia pola magnetycznego (Xu i Borovsky, 2015) [108]) daje wskazanie na ogólnie słaby i przerywany strahl oraz prawdopodobieństwo ogólnie słabego lub przerywanego połączenia magnetycznego ze Słońcem.
Podano pięć sugestii dotyczących przyszłych badań, w większości skoncentrowanych na zmianach intensywności strahla. 1) Należy zbadać związek pomiędzy zmianami intensywności strahla a stosunkiem ładunków ciężkich jonów w plazmie wiatru słonecznego. Takie informacje są ważne dla określenia charakteru zmian w połączeniu magnetycznym z koroną, które mogą mieć miejsce przy zmianie intensywności strahla i zmianie orientacji pola magnetycznego. Takie badanie umożliwiły ostatnio pomiary ciężkich jonów na pokładzie Solar Orbiter z rozdzielczością czasową ≤30 s (Owen et al., 2020 [73]), pomiary, które są o rząd wielkości szybsze niż na poprzednich misjach związanych z wiatrem słonecznym. 2) Badanie zmian strahla na statkach kosmicznych bliżej Słońca jest ważne dla lepszego określenia interpretacji zmian jego intensywności. Szczególnie pomocna będzie analiza z Parker Solar Probe, zwłaszcza po zebraniu pokaźnej bazy danych. 3) Często w 1 AU obserwuje się nagłą zmianę w intensywności anty-strahla: zmiana ta może być jednoczesna ze zmianą strahla lub może wystąpić bez jego zmiany (przykład tego można zobaczyć o 3.37 UT na niebieskiej krzywej w górnym panelu Ilustracji 7). Statystyczne badanie zmian intensywności anty-strahla może zapewnić wgląd w fizykę zmian strahla. Jest to również metoda badania topologii magnetycznej poza 1 AU. 4) Powiązanie zmian intensywności strahla z rozpraszaniem gwizdowym, dokonane w obecnej pracy, oparte jest na modelu rozpraszania gwizdowego w heliosferze, który nie uwzględnia czynników, które mogłyby kontrolować amplitudę gwizdowo-turbulencyjną w wietrze słonecznym. Poprawa przewidywania parametrów wiatru słonecznego, które kontrolują amplitudę turbulencji gwizdowych w wietrze słonecznym i wynikające z niej rozpraszanie elektronów jest potrzebna do lepszej oceny roli gwizdów w obserwowanych zmianach intensywności strahli. 5) Innym możliwym powodem, dla którego strahl może nie zostać wykryty w 1 AU, są niestabilności plazmowe, które mogły zakłócić strahl, (np. Gary i Saito, 2007 [36]; Kuzichev et al., 2019 [52]; Lopez et al., 2019 [61]; Vasko et al., 2019 [96]; Versharen et al., 2019 [97]; Jeong et al., 2020 [45]; Micera et al., 2020 [68]). Potrzebna jest parametryzacja progów niestabilności, a następnie dopasowanie miejsc zmiany strahli do zmian parametrów plazmy w celu przetestowania możliwości niestabilności.
Oświadczenie o dostępności danych
W niniejszym opracowaniu analizie poddano publicznie dostępne zbiory danych. Dane te można znaleźć tutaj: http://www.srl.caltech.edu/ace/ASC/.
Wkład autorów
Autorzy potwierdzają wyłączność swojego wkładu w niniejszy dokument oraz akceptują jego publikację.
Finansowanie
Praca ta była wspierana przez program NSF SHINE poprzez grant AGS-1723416, przez program NASA Heliophysics Guest Investigator Guest Investigator NASA poprzez grant NNX17AB71G, przez program NSF GEM poprzez grant AGS-2027569, oraz przez program NASA Heliophysics LWS poprzez grant NNX16AB75G.
Uznania
Autor dziękuje Stas’owi Boldyrev’owi, Ed’owi Cliver’owi, Larry’emu Kepko, Ruth Skoug, John’owi Steinberg’owi, Nikki Vial za pomoc i pomocne rozmowy.
Odniesienia
- Amaya, J., Dupus, R., Innocenti, M. E., and Lapenta, G. (2020). Visualizing and interpreting unsupervised solar wind classifications. Front. Astron. Space Sci. 7, 553207. doi:10.3389/fspas.2020.553207
- Arya, S., and Freeman, J. W. (1991). Estimates of solar wind velocity gradients between 0.3 and 1 AU based on velocity probability distributions from Helios 1 at perihelion and aphelion. J. Geophys. Res. 96, 14183. doi:10.1029/91ja01135
- Bemporad, A., Sterling, A. C., Moore, R. L., and Poletto, G. (2005). A new variety of coronal mass ejection: streamer puffs from compact ejective flares. Astrophys. J. 635, L189. doi:10.1086/499625
- Bendat, J. S., and Piersol, A. G. (1971). Random data: analysis and measurement procedures. New York, NY, United States: John Wiley, Sect. 4.8.1.
- Bercic, L., Larson, D., Whittlesey, P., Maksimovic, M., Badman, S. T., Landi, S., et al. (2020). Coronal electron temperature inferred from the strahl electrons in the inner heliosphere: Parker Solar Probe and Helios observations. Astrophys. J. 892, 88. doi:10.3847/1538-4357/ab7b7a
- Beyer, W. H. (1966). Handbook of Tables for Probability and statistics. Sect. IX. Cleveland, OH, United States: Chemical Rubber Company.
- Bloch, T., Watt, C., Owens, M., McInnes, L., and Macneil, A. R. (2020). Data-driven classification of coronal hole and streamer belt solar wind. Solar Phys. 295, 41. doi:10.1007/s11207-020-01609-z
- Boldyrev, S., Forest, C., and Egedal, J. (2020). Electron temperature of the solar wind. Proc. Natl. Acad. Sci. United States 117, 9232. doi:10.1073/pnas.1917905117
- Boldyrev, S., and Horaites, K. (2019). Kinetic theory of the electron strahl in the solar wind. MNRAS 489, 3412. doi:10.1093/mnras/stz2378
- Borovsky, J. E. (2010). On the variations of the solar wind magnetic field about the Parker spiral direction. J. Geophys. Res. 115, A09101. doi:10.1029/2009ja015040
- Borovsky, J. E. (2016). The plasma structure of coronal hole solar wind: origins and evolution. J. Geophys. Res. 121, 5055. doi:10.1002/2016ja022686
- Borovsky, J. E. (2017). Time-integral correlations of multiple variables with the relativistic-electron flux at geosynchronous orbit: the strong roles of the substorm-injected electrons and the ion plasma sheet. J. Geophys. Res. 122, 11961. doi:10.1002/2017ja024476
- Borovsky, J. E. (2018). On the origin of the intercorrelations between solar-wind variables. J. Geophys. Res. 123, 20. doi:10.1002/2017ja024650
- Borovsky, J. E. (2020a). The magnetic structure of the solar wind: ionic composition and the electron strahl. Geophys. Res. Lett. 47, e2019GL084586. doi:10.1029/2019gl084586
- Borovsky, J. E. (2020b). Plasma and magnetic-field structure of the solar wind at inertial-range scale sizes discerned from statistical examinations of the time-series measurements. Front. Astron. Space Sci. 7, 20. doi:10.3389/fspas.2020.00020
- Borovsky, J. E., and Gary, S. P. (2014). How important are the alpha-proton relative drift and the electron heat flux for the proton heating of the solar wind in the inner heliosphere?. J. Geophys. Res. 119, 5210. doi:10.1002/2014ja019758
- Borovsky, J. E., and Steinberg, J. T. (2006). The freestream turbulence effect in solar-wind/magnetosphere coupling: analysis through the solar cycle and for various types of solar wind. Geophys. Monog. Ser. 167, 59. doi:10.1029/167gm07
- Bruno, R., and Bavassano, B. (1997). On the winding of the IMF spiral for slow and fast wind within the inner heliosphere. Geophys. Res. Lett. 24, 2267. doi:10.1029/97gl02183
- Burkholder, B. L., Otto, A., Delamere, P. A., and Borovsky, J. E. (2019). Magnetic connectivity in the corona as a source of structure in the solar wind. J. Geophys. Res. 124, 32. doi:10.1029/2018ja026132
- Burlaga, L. F., and Ness, N. F. (1997). Global patterns of heliospheric magnetic field polarities and elevation angles: 1990 through 1995. J. Geophys. Res. 102, 19731. doi:10.1029/97ja01568
- Camporeale, E., Care, A., and Borovsky, J. E. (2017). Classification of solar wind with machine learning. J. Geophys. Res. 122, 10910. doi:10.1002/2017ja024383
- Chollet, E. E., and Giacalone, J. (2011). Evidence of confinement of solar-energetic particles to interplanetary magnetic field lines. Astrophys. J. 728, 64. doi:10.1088/0004-637x/728/1/64
- Chollet, E., Skoug, R., Steinberg, J., Crooker, N., and Giacalone, J. (2010). Reconnection and disconnection: observations of suprathermal electron heat flux dropouts. AIP Conf. Proc. 1216, 600. doi:10.1063/1.3395937
- Cliver, E. W., and Ling, A. G. (2007). Electrons and protons in solar energetic particle events. Astrophys. J. 658, 1349. doi:10.1086/511737
- Crooker, N. U., Appleton, E. M., Schwadron, N. A., and Owens, M. J. (2010). Suprathermal electron flux peaks at stream interfaces: Signature of solar wind dynamics or tracer for open magnetic flux transport on the Sun?. J. Geophys. Res. 115, A11101. doi:10.1029/2008GM000822
- Crooker, N. U., Gosling, J. T., and Kahler, S. W. (2002). Reducing heliospheric magnetic flux from coronal mass ejections without disconnection. J. Geophys. Res. 107, 1028. doi:10.1029/2001ja000236
- Crooker, N. U., Huang, C.-L., Lamassa, S. M., Larson, D. E., Kahler, S. W., and Spence, H. E. (2004). Heliospheric plasma sheets. J. Geophys. Res. 109, A03107. doi:10.1029/2003ja010170
- Crooker, N. U., and Owens, M. J. (2012). Interchange reconnection: remote sensing of solar signature and role in heliospheric magnetic flux budget. Space Sci. Rev. 172, 201. doi:10.1007/s11214-011-9748-1
- Crooker, N. U., and Pagel, C. (2008). Residual strahls in solar wind electron dropouts: signatures of magnetic connection to the Sun, disconnection, or interchange reconnection? J. Geophys. Res. 113, A02106. doi:10.1029/2007ja012421
- Elliott, H. A., Henney, C. J., McComas, D. J., Smith, C. W., and Vasquez, B. J. (2012). Temporal and radial variation of the solar wind temperature-speed relationship. J. Geophys. Res. 117, A09102. doi:10.1029/2011ja017125
- Feldman, W. C., Asbridge, J. R., Bame, S. J., Gary, S. P., Montgomery, M. D., and Zink, S. M. (1976). Evidence for the regulation of solar wind heat flux at 1 AU. J. Geophys. Res. 81, 5207. doi:10.1029/ja081i028p05207
- Fisk, L. A. (2001). On the global structure of the heliospheric magnetic field. J. Geophys. Res. 106, 15849. doi:10.1029/2000ja000117
- Forsyth, R. J., Balogh, A., Smith, E. J., Erdös, G., and McComas, D. J. (1996). The underlying Parker spiral structure in the Ulysses magnetic field observations, 1990-1994. J. Geophys. Res. 101, 395. doi:10.1029/95ja02977
- Foullon, C., Lavraud, B., Luhmann, J. G., Farrugia, C. J., Retino, A., Simunac, K. D. C., et al. (2011). Plasmoid releases in the heliospheric current sheet and associated coronal hole boundary layer evolution. Astrophys. J. 737, 16. doi:10.1088/0004-637x/737/1/16
- Gary, S. P., Feldman, W. C., Forslund, D. W., and Montgomery, M. D. (1975). Electron heat flux instabilities in the solar wind. Geophys. Res. Lett. 2, 79–82. doi:10.1029/gl002i003p00079
- Gary, S. P., and Saito, S. (2007). Broadening of solar wind strahl pitch-angles by the electron/electron instability: particle-in-cell simulations. Geophys. Res. Lett. 34, L14111. doi:10.1029/2007gl030039
- Georgieva, K., Kirov, B., Javaraiah, J., and Krasteva, R. (2005). Solar rotation and solar wind-magnetosphere coupling. Planet. Space Sci. 53, 197. doi:10.1016/j.pss.2004.09.045
- Gloeckler, G., Cain, J., Ipavich, F. M., Tums, E. O., Bedini, P., Fisk, L. A., et al. (1998). Investigation of the composition of solar and interstellar matter using solar wind and pickup ion measurements with SWICS and SWIMS on the ACE spacecraft. Space Sci. Rev. 86, 497. doi:10.1007/978-94-011-4762-0_18
- Gosling, J. T., de Koning, C. A., Skoug, R. M., Steinberg, J. T., and McComas, D. J. (2004a). Dispersionless modulations in low-energy solar electron bursts and discontinuous changes in the solar wind electron strahl. J. Geophys. Res. 109, A05102. doi:10.1029/2003ja010338
- Gosling, J. T., Skoug, R. M., McComas, D. J., and Mazur, J. E. (2004b). Correlated dispersionless structure in suprathermal electrons and solar energetic ions in the solar wind. Astrophys. J. 614, 412. doi:10.1086/423368
- Gosling, J. T., Skoug, R. M., McComas, D. J., and Smith, C. W. (2005). Magnetic disconnection from the Sun: observations of a reconnection exhaust in the solar wind at the heliospheric current sheet. Geophys. Res. Lett. 32, L05105. doi:10.1029/2005gl022406
- Gosling, J. T., and Skoug, R. M. (2002). On the origin of radial magnetic fields in theheliosphere. J. Geophys. Res. 107, 1327. doi:10.1029/2002ja009434
- Hammond, C. M., Feldman, W. C., McComas, D. J., Phillips, J. L., and Forsyth, R. J. (1996). Variation of electron-strahl width in the high-speed solar wind: ulyssesobservations. Aston. Astrophys. 316, 350–354.
- Heidrich-Meisner, V., Berger, L., and Wimmer-Schweingruber, R. F. (2020). Proton-proton collisional age to order solar wind types. Astron. Astrophys. 636, A103. doi:10.1051/0004-6361/201937378
- Jeong, S.-Y., Verscharen, D., Wicks, R. T., and Fazakerley, A. N. (2020). A quasi-linear diffusion model for resonant wave-particle instability in homogeneous plasma. Astrophys. J. 902, 128. doi:10.3847/1538-4357/abb099
- Kallenrode, M.-B., and Švestka, Z. (1994). The participation of nuclei in type-III-related electron streams. Sol. Phys. 155, 121. doi:10.1007/bf00670735
- Kepko, L., and Spence, H. E. (2003). Observations of discrete, global magnetospheric oscillations directly driven by solar wind density variations. J. Geophys. Res. 108, 1257. doi:10.1029/2002ja009676
- Kepko, L., Viall, N. M., Antiochos, S. K., Lepri, S. T., Kasper, J. C., and Weberg, M. (2016). Implications of L1 observations for slow solar wind formation by solar reconnection. Geophys. Res. Lett. 43, 4089. doi:10.1002/2016gl068607
- Kepko, L., and Viall, N. M. (2019). The source, significance, and magnetospheric impact of periodic density structures within stream interaction regions. J. Geophys. Res. 124, 2019JA026962. doi:10.1029/2019ja026962
- King, J. H., and Papitashvili, N. E. (2005). Solar wind spatial scales in and comparisons of hourly Wind and ACE plasma and magnetic field data. J. Geophys. Res. 110, 2104. doi:10.1029/2004ja010649
- Krall, N. A., and Trivelpiece, A. W. (1973). Principles of plasma physics. New York, NY, United States: McGraw-Hill.
- Kuzichev, I. V., Vasko, I. Y., Soto-Chavez, A. R., Tong, Y., Artemyev, A. V., Bale, S. D., et al. (2019). Nonlinear evolution of the whistler heat flux instability. Astrophys. J. 882, 81. doi:10.3847/1538-4357/ab3290
- Lavraud, B., Fargette, N., Reville, V., Szabo, A., Huang, J., Ruillard, A. P., et al. (2020). The heliospheric current sheet and plasma sheet during Parker Solar Probe’s first orbit. Astrophys. J. Lett. 894, L19. doi:10.3847/2041-8213/ab8d2d
- Lavraud, B., Gosling, J. T., Rouillard, A. P., Fedorov, A., Opitz, A., Sauvaud, J.-A., et al. (2009). Observations of a complex solar wind reconnection exhaust from spacecraft separated by over 1800 RE. Sol. Phys. 256, 379. doi:10.1007/s11207-009-9341-x
- Lemaire, J. (2010). Half a century of kinetic solar wind models. AIP Conf. Proc. 1216, 8. doi:10.1063/1.3395971
- Lemons, D. S., and Feldman, W. C. (1983). Collisional modification to the exospheric theory of solar wind halo electron pitch angle distributions. J. Geophys. Res. 88, 6881. doi:10.1029/ja088ia09p06881
- Li, C., Sun, L. P., Wang, X. Y., and Dai, Y. (2013). Coronal magnetic topology and the production of solar impulsive energetic electrons. Astron. Astrophys. 556, L2. doi:10.1051/0004-6361/201322072
- Li, H., Wang, C., Tu, C., and Xu, F. (2020). Machine learning approach for solar wind categorization. Earth Space Sci. 7, e2019EA000997. doi:10.1029/2019ea000997
- Lin, R. P., and Kahler, S. W. (1992). Interplanetary magnetic field connection to the Sun during electron heat flux dropouts in the solar wind. J. Geophys. Res. 97, 8203. doi:10.1029/92ja00230
- Lockwood, M. (2013). Reconstruction and prediction of variations in the open solar magnetic flux and interplanetary conditions. Living Rev. Solar Phys. 10, 4. doi:10.12942/lrsp-2013-4
- Lopez, R. A., Shaaban, S. M., Lazar, M., Poedts, S., Yoon, P. H., Micera, A., et al. (2019). Particle-in-cell simulations of the whistler heat-flux instability in solar wind conditions. Astrophys. J. Lett. 882, L8.
- Lopez, R. E., and Freeman, J. W. (1986). Solar wind proton temperature-velocity relationship. J. Geophys. Res. 91, 1701. doi:10.1029/ja091ia02p01701
- Louarn, P., Diéval, C., Génot, V., Lavraud, B., Opitz, A., Fedorov, A., et al. (2009). On the temporal variability of the “strahl” and its relationship with solar wind characteristics: STEREO SWEA observations. Sol. Phys. 259, 311–321. doi:10.1007/s11207-009-9402-1
- Maksimovic, M., Zouganelis, I., Chaufray, J.-Y., Issautier, K., Scime, E. E., Littleton, J. E., et al. (2005). Radial evolution of the electron distribution functions in the fast solar wind between 0.3 and 1.5 AU. J. Geophys. Res. 110, A09104. doi:10.1029/2005ja011119
- Mazur, J. E., Mason, G. M., Dwyer, J. R., Giacalone, J., Jokipii, J. R., and Stone, E. C. (2000). Interplanetary magnetic field line mixing deduced from impulsive solar flare particles. Astrophys. J. 532, L79. doi:10.1086/312561
- McComas, D. J., Bame, S. J., Barker, P., Feldman, W. C., Phillips, J. L., Riley, P., et al. (1998). Solar wind electron proton alpha monitor (SWEPAM) for the advanced composition explorer. Space Sci. Rev. 86, 563. doi:10.1007/978-94-011-4762-0_20
- McComas, D. J., Gosling, J. T., Phillips, J. L., Bame, S. J., Luhmann, J. G., and Smith, E. J. (1989). Electron heat flux dropouts in the solar wind: evidence for interplanetary magnetic field reconnection?. J. Geophys. Res. 94, 6907. doi:10.1029/ja094ia06p06907
- Micera, A., Zhukov, A. N., López, R. A., Innocenti, M. E., Lazar, M., Boella, E., et al. (2020). Particle-in-cell simulation of whistler heat-flux instabilities in the solar wind: heat-flux regulation and electron halo formation. Astrophys. J. Lett. 903, L23. doi:10.3847/2041-8213/abc0e8
- Murphy, N., Smith, E. J., and Schwadron, N. A. (2002). Strongly underwound magnetic fields in co-rotating rarefaction regions: observations and implications. Geophys. Res. Lett. 29, 2066. doi:10.1029/2002gl015164
- Ness, N. F., and Wilcox, J. M. (1966). Extension of the photospheric magnetic field into interplanetary space. Astrophys. J. 143, 23. doi:10.1086/148473
- Neugebauer, M., Reisenfeld, D., and Richardson, I. G. (2016). Comparison of algorithms for determination of solar wind regimes. J. Geophys. Res. 121, 8215. doi:10.1002/2016ja023142
- Neugebauer, M., Steinberg, J. T., Tokar, R. L., Barraclough, B. L., Dors, E. E., Wiens, R. C., et al. (2003). Genesis on-board determination of the solar wind flow regime. Space Sci. Rev. 105, 661. doi:10.1023/a:1024478129261
- Owen, C. J., Bruno, R., Livi, S., Louarn, P., and Al Janabi, K. (2020). The solar orbiter solar wind analyzer (SWA) suite. Astron. Astrophys. 642, A16. doi:10.1051/0004-6361/201937259
- Pagel, C., Crooker, N. U., and Larson, D. E. (2005a). Assessing electron heat flux dropouts as signatures of magnetic field line disconnection from the sun. Geophys. Res. Lett. 32, L14105. doi:10.1029/2005gl023043
- Pagel, C., Crooker, N. U., Larson, D. E., Kahler, S. W., and Owen, M. J. (2005b). Understanding electron heat flux signatures in the solar wind. J. Geophys. Res. 110, A01103. doi:10.1029/2004ja010767
- Parker, E. N. (1958). Dynamics of the interplanetary gas and magnetic fields. Astrophys. J. 128, 664. doi:10.1086/146579
- Pierrard, V., Lazar, M., and Schlickeiser, R. (2011). Evolution of the electron distribution function in the whistler wave turbulence of the solar wind. Sol. Phys. 269, 421. doi:10.1007/s11207-010-9700-7
- Pierrard, V. (2012). Solar wind electron transport: interplanetary electric field and heat conduction. Space Sci. Rev. 172, 315. doi:10.1007/s11214-011-9743-6
- Pilipp, W. G., Miggenrieder, H., Montgomery, M. D., Mühlhäuser, K.-H., Rosenbauer, H., and Schwenn, R. (1987). Characteristics of electron velocity distribution functions in the solar wind derived from the Helios Plasma experiment. J. Geophys. Res. 92, 1075. doi:10.1029/ja092ia02p01075
- Reames, D. V. (1999). Particle acceleration at the Sun and in the heliosphere. Space Sci. Rev. 90, 413. doi:10.1023/a:1005105831781
- Reisenfeld, D. B., Steinberg, J. T., Barraclough, B. L., Dors, E. E., Weins, R. C., Neugebauer, M., et al. (2003). Comparison of the Genesis solar wind regime algorithm results with solar wind composition observed by ACE. AIP Conf. Proc. 679, 632. doi:10.1063/1.1618674
- Riley, P., and Gosling, J. T. (2007). On the origin of near-radial magnetic fields in the heliosphere: numerical simulations. J. Geophys. Res. 112, A06115. doi:10.1029/2006ja012210
- Rouillard, A. P., Davies, J. A., Lavraud, B., Forsyth, R. J., Savani, N. P., Bewsher, D., et al. (2010). Intermittent release of transients in the slow solar wind: 1. Remote sensing observations. J. Geophys. Res. 115, A04103. doi:10.1029/2009ja014471
- Rouillard, A. P., Kouloumvakos, A., Vourlidas, A., Kasper, J., Bale, S., Raouafi, N.E., et al. (2020). Relating streamer flows to density and magnetic structures at the parker solar robe. Astrophys. J. Suppl. Ser. 246, 37. doi:10.3847/1538-4365/ab579a
- Saito, S., and Gary, S. P. (2007). All whistlers are not created equally: scattering of strahl electrons in the solar wind via particle-in-cell simulations. Geophys. Res. Lett. 34, L01102. doi:10.1029/2006gl028173
- Sanchez-Diaz, E., Rouillard, A. P., Lavraud, B., Kilpua, E., and Davies, J. A. (2019). In Situ measurements of the variable slow solar wind near sector boundaries. Astrophys. J. 882, 51. doi:10.3847/1538-4357/ab341c
- Schwenn, R., Muhlhauser, K.-H., Marsch, E., and Rosenbauer, H. (1981). Two states of the solar wind at the time of solar activity minimum II. Radial gradients of plasma parameters in fast and slow streams. Solar wind four, MPAE-W-100-81-31. Lindau, Germany: Max Planck Institut fur Aeronomie. 126.
- Scudder, J. D., and Olbert, S. (1979). A theory of local and global processes which affect solar wind electrons, 1. The origin of typical 1 AU velocity distribution functions-Steady state theory. J. Geophys. Res. 84, 2755. doi:10.1029/ja084ia06p02755
- Sheeley, N. R., Lee, D. D.-H., Casto, K. P., Wang, Y.-M., and Rich, N. B. (2009). The structure of streamer blobs. ApJ 694, 1471. doi:10.1088/0004-637x/694/2/1471
- Sheeley, N. R., and Rouillard, A. P. (2010). Tracking streamer blobs into the heliosphere. ApJ 715, 300. doi:10.1088/0004-637x/715/1/300
- Smith, C. W., and Bieber, J. W. (1991). Solar cycle variation of the interplanetary magnetic field spiral. Astrophys. J. 370, 435. doi:10.1086/169830
- Smith, C. W., Acuna, M. H., Burlaga, L. F., L’Heureux, J., Ness, N. F., and Scheifele, J. (1998). The ACE magnetic fields experiment. Space Sci. Rev. 86, 611. doi:10.1023/a:1005092216668
- Steinacker, J., and Miller, J. A. (1992). Stochastic gyroresonant electron acceleration in a low-beta plasma. I – interaction with parallel transverse cold plasma waves. Astrophys. J. 393, 764. doi:10.1086/171544
- Tang, B., Zank, G. P., and Kolobov, V. (2018). Numerical modeling of electron transport in solar wind: effects of whistler turbulence and Coulomb collisions. J. Phys. Conf. Ser. 1100, 012025. doi:10.1088/1742-6596/1100/1/012025
- Trenchi, L., Bruno, R., Telloni, D., D’amicis, R., Marcucci, M. F., Zurbuchen, T. H., et al. (2013). Solar energetic particle modulations associated with coherent magnetic structures. Astrophys. J. 770, 11. doi:10.1088/0004-637x/770/1/11
- Vasko, I. Y., Krasnoselskikh, V., Tong, Y., Bale, S. D., Bonnell, J. W., and Mozer, F. S. (2019). Whistler fan instability driven by strahl electrons in the solar wind. Astrophys. J. Lett. 871, L29.
- Versharen, D., Chandran, B. D. G., Jeong, S.-Y., Salem, C. S., Pulupa, M. P., and Bale, S. D. (2019). Self-induced scattering of strahl electrons in the solar wind. Astrophys. J. 886, 136. doi:10.3847/1538-4357/ab4c30
- Veselovsky, I. S., Lukashenko, A. T., and Kaportseva, K. B. (2018). Classification scheme for solar wind. Phys. Atom. Nuclei 81, 766. doi:10.1134/s1063778818050186
- Viall, N. M., and Borovsky, J. E. (2020). Nine outstanding questions of solar wind physics. J. Geophys. Res. 125, e2018JA026005. doi:10.1029/2018ja026005
- Viall, N. M., Kepko, L., and Spence, H. E. (2009). Relative occurrence rates and connection of discrete frequency oscillations in the solar wind density and dayside magnetosphere. J. Geophys. Res. 114, A01201. doi:10.1029/2008ja013334
- Viall, N. M., Spence, H. E., Vourlidas, A., and Howard, R. (2010). Examining periodic solar-wind density structures observed in the SECCHI Heliospheric imagers. Sol. Phys. 267, 175. doi:10.1007/s11207-010-9633-1
- Viall, N. M., and Vourlidas, A. (2015). Periodic density structures and the origin of the slow solar wind. Astrophys. J. 807, 176. doi:10.1088/0004-637x/807/2/176
- Viñas, A. F., Gurgiolo, C., Nieves-Chinchilla, T., Gary, S. P., and Goldstein, M. L. (2010). Whistler waves driven by anisotropic strahl velocity distributions: cluster observations. AIP Conf. Proc. 1216, 265. doi:10.1063/1.3395852
- Wang, Y.-M., Sheeley, N. R., Howard, R. A., Rich, N. B., and Lamy, P. L. (1999). Streamer disconnection events observed with the LASCO coronagraph. Geophys. Res. Lett. 26, 1349. doi:10.1029/1999gl900177
- Wang, Y.-M., Sheeley, N. R., Socker, D. G., Howard, R. A., and Rich, N. B. (2000). The dynamical nature of coronal streamers. J. Geophys. Res. 105, 25113. doi:10.1029/2000ja000149
- Wang, L., Lin, R. P., Krucker, S., and Mason, G. M. (2012). A statistical study of solar electron events over one solar cycle. Astrophys. J. 759, 69. doi:10.1088/0004-637x/759/1/69
- Wibberenz, G., and Cane, H. V. (2006). Multi-spacecraft observations of solar flare particles in the inner heliosphere. Astrophys. J. 650, 1199. doi:10.1086/506598
- Xu, F., and Borovsky, J. E. (2015). A new four-plasma categorization scheme for the solar wind. J. Geophys. Res. 120, 70. doi:10.1002/2014ja020412
- Zhao, L., Zurbuchen, T. H., and Fisk, L. A. (2009). Global distribution of the solar wind during solar cycle 23: ACE observations. Geophys. Res. Lett. 36, L14104. doi:10.1029/2009gl039181
- Zhao, L., Landi, E., Kocher, M., Lepri, S. T., Fisk, L. A., and Zrbuchen, T. H. (2016). Anomalously low C6+/C5+ ratio in solar wind: ACE/SWICS observation. AIP Conf. Proc. 1720, 020006. doi:10.1063/1.4943807
- Jockers, K. (1970). Solar wind models based on exospheric theory. Astron. Astrophys. 6, 219.
Konflikt interesów: Autor oświadcza, że badania zostały przeprowadzone przy braku jakichkolwiek związków komercyjnych lub finansowych, które mogłyby być interpretowane jako potencjalny konflikt interesów.
Copyright © 2021 Borovsky. Jest to artykuł o otwartym dostępie na warunkach Creative Commons Attribution License (CC BY). Wykorzystanie, dystrybucja lub reprodukcja na innych forach jest dozwolona, pod warunkiem, że oryginalny autor (autorzy) i właściciel (właściciele) praw autorskich są uznani i że oryginalna publikacja w tym czasopiśmie jest cytowana zgodnie z przyjętą praktyką akademicką. Nie zezwala się na użycie, dystrybucję lub reprodukcję, która nie jest zgodna z tymi warunkami.
Przetłumaczył z angielskiego i edytował w LibreOffice: Łukasz Buczyński (pirogronian.smallhost.pl) – przy pomocy deepl.com.
Dzięki za zainteresowanie tematem ale
przydałaby by się opcja kliknięcia w odnośnik do przeskoczenia do konkretnego rozdziału pracy bo ciężko się to czyta na telefonie.
Wiem, próbowałem to zrobić w wersji PDF ale nie wyszło a potem już mi się nie chciało… Chodzi tylko o odnośniki do rozdziałów czy też do bibliografii?