Poniżej jest kolejne tłumaczenie pracy naukowej dotyczącej wiatru słonecznego. Jest to ciąg dalszy moich poszukiwań aktualnej wiedzy na jego temat, w szczególności jego właściwości elektrycznych.

Wersje plikowe do pobrania: PDF, ODT. Poniżej wersja online.

Przetłumaczono z: https://www.frontiersin.org/articles/10.3389/fspas.2021.690005/full

---

frontiers in Astronomy and Space Science

ORIGINAL RESEARCH

published: 08 June 2021

doi: 10.3389/fspas.2021.690005

Struktura Elektronowa Wiatru Słonecznego

Joseph E. Borovsky ¹*, Jasper S. Halekas ² i Phyllis L. Whittlesey ³

¹Center for Space Plasma Physics, Space Science Institute, Boulder, CO, United States, ²Department of Physics and Astronomy, University of Iowa, Iowa City, IA, United States, ³Space Science Lab, University of California, Berkeley, CA, United States

Otwarty dostęp

Edytor:

Daniele Telloni,

National Institute of Astrophysics

(INAF), Italy

Recenzja:

Tommaso Alberti,

Institute for Space Astrophysics and

Planetology (INAF), Italy

Olga Malandraki,

National Observatory of Athens,

Greece

*Kontakt:

Joseph E. Borovsky

jborovsky@spacescience.org

Specjalizacja:

Ten artykuł przedłożono do Space Physics, sekcji czasopisma Frontiers in Astronomy and Space Sciences

Otrzymano: 01 April 2021

Zaakceptowano: 24 May 2021

Opublikowano: 08 June 2021

Cytatowanie:

Borovsky JE, Halekas JS i Whittlesey PL (2021) The Electron Structure of the Solar Wind.

Front. Astron. Space Sci. 8:690005.

doi: 10.3389/fspas.2021.690005

Zbadano pomiary w serii czasowej gęstości liczbowej n_core i temperatury T_core populacji elektronóœ rdzeniowych wiatru słonecznego odległości w 1 AU i w 0,13 AU przy użyciu pomiarów z sond, odpowiednio, WIND i Parker Solar Probe. Analiza statystyczna pomiarów n_core i T_core w 1 AU wykazała, że struktura przestrzenna elektronów rdzeniowych w wietrze słonecznym jest związana ze strukturą tub magnetycznych wiatru słonecznego; ta struktura elektronowa charakteryzuje się skokami wartości n_core i T_core przy przechodzeniu z jednej rury przepływu magnetycznego do następnej. Te same rodzaje skoków pomiędzy tubami przepływu są widoczne dla T_core w 0,13 AU. Niektóre modele międzyplanetarnego potencjału elektrycznego heliosfery przewidują, że T_core jest bezpośrednią miarą lokalnego potencjału elektrycznego w heliosferze. Jeśli tak, to skoki obserwowane w T_core reprezentują skoki potencjału elektrycznego pomiędzy tubami przepływu. To może sugerować, że międzyplanetarny potencjał elektryczny (i jego wpływ na radialną ewolucję jonów i elektronów wiatru słonecznego od Słońca) działa niezależnie w każdej tubie przepływu heliosfery.

Słowa kluczowe: wiatr słoneczny, heliosfera, potencjał międzyplanetarny, korona, struktura magnetyczna

WPROWADZENIE

Struktura magnetyczna wiatru słonecznego w odległości 1 AU jest dobrze zaobserwowana, z wszechobecnymi silnymi arkuszami prądowymi (magnetyczne nieciągłości kierunkowe) (Siscoe et al., 1968 [100]; Burlaga i Ness, 1969 [23]; Mariani et al., 1973 [75]; Vasquez et al., 2007 [106]) dzielącymi pole magnetyczne i plazmę na liczne domeny przestrzenne. Na przestrzeni lat obserwacje zachowania strumieni i anizotropii cząstek energetycznych, strumienia (strahlu) elektronów, plazmy protonowej, masowego przepływu protonów oraz stosunku jonów alfa do protonów doprowadziły do powstania obrazu struktury magnetycznej, w której arkusze prądowe dzielą pole na włókna lub spaghetti rur strumienia magnetycznego (Bartley et al., 1966 [3]; McCracken i Ness, 1966 [79]; Michel, 1967 [83]; Bruno et al., 2001 [21]; Borovsky, 2008 [12]; Greco et al., 2008 [42]; Riazantseva et al., 2017 [94]; Pecora et al., 2019 [89]). Istnieją jednak inne przedstawienia struktury magnetycznej wiatru słonecznego, na przykład domieszka tub strumienia, plazmoidów, wysp magnetycznych i zlokalizowanych struktur magnetycznych (np. Khaborova et al., 2015 [56]; Khaborova et al., 2016 [57]; Adhikari et al., 2019 [1]; Malandraki et al., 2019 [73]; Khaborova et al., 2020 [54]), co dobrze obrazuje ilustracja 24C w przeglądzie Khabarova et al. (2021) [55]. Z pewnością wiadomo, że plamy plazmy o zamkniętym polu można znaleźć w plazmie wiatru słonecznego pochodzącej z koronalnych odgałęzień streamerów (Wang et al., 1999 [111]; Sheeley i Rouillard, 2010 [99]; Viall et al., 2010 [110]; Viall i Vourlidas, 2015 [108]; Kepko et al., 2016 [53]; Di Matteo et al., 2019 [30]). Pokrewnie, plazma z obszaru sektora odwracania (w którym znajduje się heliosferyczny arkusz prądowy) ma tendencję do posiadania pól magnetycznych, które są mniej zorientowane na spiralę Parkera i ma tendencję do posiadania słabszego strahlu elektronowego (Borovsky, 2021 [20]), obie cechy będące wskaźnikiem impulsywnej emisji plazmy ze Słońca ze słabymi połączeniami magnetycznymi ze Słońcem. W niebędącym wyrzutowym wietrze słonecznym tuby strumienia magnetycznego meandrują wokół kierunku spirali Parker (Borovsky, 2010 [13]). Wiadomo również, że istnieje struktura plazmy w wietrze słonecznym na wysokości 1 AU, która jest związana ze strukturą magnetyczną: zmiany (skoki) w wielkościach plazmy współwystępują z silnymi arkuszami prądów, które są granicami pomiędzy tubami strumienia magnetycznego. Wskazuje to, że własności plazmy różnią się w zależności od tuby strumienia magnetycznego.

Pochodzenie tekstury strumienia wiatru słonecznego jest niepewne: głównym pytaniem jest, jakie części tej struktury powstają lokalnie w wietrze słonecznym daleko od Słońca, a jakie są „skamieniałościami” z korony słonecznej (Neugebauer i Giacalone, 2010 [85]; Li i Qin, 2011 [67]; Owens et al., 2011 [88]; Neugebauer i Giacalone, 2015 [86]; Telloni et al., 2016 [101]; Tu et al., 2016 [104]; Viall i Borovsky, 2020 [107]). Pomysły w literaturze, dotyczące genezy arkusza prądowego, obejmują 1) formowanie go przez nieliniowe stopnie podróżujących na zewnątrz fal Alfvéna (Malara et al., 1996 [74]; Vasquez i Hollweg, 1999 [105]), 2) jego formowanie i niszczenie w aktywnej turbulencji MHD (Dmitruk et al., 2004 [31]; Greco et al., 2010 [43], Greco et al, 2016 [44]), 3) tuby strumieniowe, pozostałe z korony, unoszone na zewnątrz z wiatrem słonecznym (Borovsky, 2008 [12]; Huang et al., 2014 [48]; Burkholder et al., 2019 [22]; Eselevich, 2019 [35]), oraz 4) pozostałości rozpadłych turbulencji w pobliżu Słońca, które są unoszone na zewnątrz z wiatrem słonecznym (np. Dobrowolny et al., 1980 [32]; Matthaeus et al., 2012 [77]; Servidio et al., 2014 [98]; Telloni et al., 2016 [101]). Mechanizmy (1) i (2) mają strukturę tworzoną in situ w wietrze słonecznym; mechanizm (4) ma strukturę tworzoną w wietrze słonecznym w pobliżu Słońca; a mechanizm (3) ma strukturę tworzoną w koronie.

Dla oceny wpływu ustaleń niniejszego studium elementem do rozważenia jest przetrwanie arkuszy prądowych i tub strumieniowych od korony do 1 AU. W górnej koronie słonecznej plazma jest dzielona na magnetyczne tuby strumieniowe przez arkusze prądowe (Close et al., 2003 [26]; Close et al., 2005 [27]; DeForest et al., 2018 [29]; Burkholder et al., 2019 [22]). Trzy obserwacje dostarczają dowodów na przetrwanie niektórych arkuszy prądowych. 1) Widoczne są arkusze prądowe w odległości 1 AU, które mają silne skoki w stosunku liczby-do-gęstości alfa do liczby protonów α/p w poprzek nich (Borovsky, 2020a [16]). Takie granice α/p w składzie jonów mogą powstać tylko w koronie, a nie w wietrze słonecznym z dala od Słońca: stąd te konkretne arkusze prądowe, widoczne w 1 AU, są skamielinami (reliktami) z korony. 2) Podobnie, arkusze prądowe w 1 AU są widziane wraz ze skokami intensywności strahlu elektronów (Borovsky, 2020a [16]): dla tych arkuszy prądowych skok strahla jest wskazówką, że arkusz prądowy jest spójny na drodze do Słońca (Gosling et al., 2004a [38],b [39]; Borovsky, 2020a [20]). Skoki intensywności strahla pomiędzy tubami sugerują, że różne tuby strumieniowe w magnetycznym spaghetti łączą się magnetycznie z różnymi miejscami na Słońcu (Gosling et al., 2004a [38], b [39]; Borovsky, 2021 [20]). (Podobnie, zobarz: Trenchi et al. (2013a [102], b [103]) dla spójności wskazywanej przez obserwacje energetycznych cząstek). 3) Badanie kompresji i rozrzedzania struktury magnetycznej w wietrze słonecznym w 1 AU (Borovsky i Denton, 2016 [8]; Borovsky, 2020d [19]) wskazuje, że arkusze prądowe i tuby przepływu są długo żywe (wiele dziesiątek godzin do wieku plazmy wiatru słonecznego). Jeśli tuby przepływu wiatru słonecznego miałyby ulec zniszczeniu, to dwoma możliwymi mechanizmami ich destrukcji są turbulencja i rekoneksja. Pogląd, że tuby przepływu ze Słońca mogłyby zostać zniszczone przez działanie turbulencji w wietrze słonecznym, został przetestowany poprzez ilościowe określenie ilości turbulentnego mieszania (rozciągania i składania), które występuje w wietrze słonecznym pomiędzy 0.3 a 1 AU (Borovsky, 2012b [15]): nie znaleziono dowodów na mieszanie. Podobnie, okresowe struktury wiatru słonecznego o skalach przestrzennych w „podzakresie inercyjnym” przeżywają do 1 AU i dalej, nie będąc niszczone przez turbulencje (Kepko i Spence, 2003 [51]; Viall et al., 2009 [109]; Di Matteo et al., 2019 [30]; Kepko i Viall, 2019 [52]; Birch i Hargreaves, 2020a [4], b [5]). Rekoneksja wydaje się również nie niszczyć arkuszy prądowych, które są ścianami rur przepływu. Zdarzenia rekoneksji wiatru słonecznego są rzadkie (Gosling et al., 2005 [40]; Phan et al., 2006 [91]; Gosling, 2012 [41]), w przeciwieństwie do wszechobecnych arkuszy prądowych. Silne arkusze prądowe wiatru słonecznego są grube (kilkaset km) (Siscoe et al., 1968 [100]; Vasquez et al., 2007 [106]; Miao et al., 2011 [82]; Borovsky i Steinberg, 2014 [9]) w porównaniu z kinetycznymi skalami jonów i elektronów (kilkadziesiąt km), niezbędnymi do zainicjowania rekoneksji w plazmie bezkolizyjnej (Hesse et al., 2001 [47]; Pritchett, 2005 [93]). Ponadto, plazma wiatru słonecznego wszędzie się z czasem rozszerza (zamiast napędzać struktury do inicjowania rekoneksji), a w alfwenicznym wietrze słonecznym występują silne spadki prędkości równolegle do B (Borovsky, 2020c [18]) w poprzek arkuszy prądowych, które mają tendencję do stabilizowania ich do rekoneksji (Roth et al., 1996 [95]; Doss et al., 2015 [33]). Ewolucja arkuszy prądowych w wietrze słonecznym może być bardziej zgodna z dyfuzją Bohma i żyro-Bohma (Perkins et al., 1993 [90]; Hannum et al., 2001 [46]; Borovsky, 2006 [11]).

Funkcja rozmieszczenia elektronów w wietrze słonecznym wykazuje ogólnie trzy odrębne składniki (np. Feldman et al., 1978 [37]; Maksimovic et al., 2005 [72]): elektrony rdzeniowe o niższej energii, elektrony halo o wyższej energii oraz bardziej energetyczny strahl, wyrównany z polem magnetycznym. Ogólnie przyjmuje się, że elektrony rdzenia wiatru słonecznego są populacją, która jest „uwięziona” przez (a) międzyplanetarną barierę potencjału pola elektrycznego, gdy elektrony rdzenia oddalają się od Słońca oraz (b) siłę lustra magnetycznego, gdy elektrony rdzenia poruszają się w kierunku Słońca (np. Lie-Svendsen i Leer, 2000 [69]; Marsch, 2006 [76]). W związku z tym, temperatura T_core zmierzonego rozkładu elektronów rdzeniowych jest związana z różnicą potencjałów elektrycznych pomiędzy miejscem pomiaru a odległą od Słońca heliosferą (Feldman et al., 1975 [36]; Boldyrev et al., 2020 [6]; Moncuquet et al., 2020 [84]) [Dla innej interpretacji T_core, patrz Scudder (2019) [97]]. Średnio, temperatura elektronów rdzenia wiatru słonecznego maleje wraz z odległością od Słońca (Pilipp et al., 1990 [92]; McComas et al., 1992 [78]; Halekas et al., 2020 [45]; Moncuquet et al., 2020 [84]), w ogólnej zgodzie z modelami egzosfery, dotyczącymi międzyplanetarnego potencjału elektrycznego φ, przy czym φ(r) maleje w magnitudzie (względem nieskończoności) wraz z odległością r od Słońca (Lemaire i Scherer, 1971 [62]; Meyer-Vernet i Issautier, 1998 [80]; Meyer-Vernet et al., 2003 [81]).

W niniejszej pracy rozszerzamy analizę plazmy i struktury magnetycznej wiatru słonecznego o badanie struktury elektronów rdzenia wiatru słonecznego i jej związku ze strukturą magnetyczną. Zbadane zostaną skoki (granice) gęstości liczbowej n_core i temperatury T_core elektronów rdzenia, statystycznie w odległości 1 AU przy użyciu sondy kosmicznej WIND i pokrótce w odległości 0.13 AU przy użyciu sondy Parker Solar Probe. Interesujący jest związek struktury elektronów rdzenia wiatru słonecznego ze strukturą magnetyczną wiatru słonecznego: zobaczymy, że wartości T_core mają tendencję do różnicowania się w zależności od tuby przepływu.

Jeśli T_core jest miarą lokalnego potencjału elektrycznego φ w wietrze słonecznym, to przestrzenne zmiany T_core reprezentują przestrzenne zmiany potencjału elektrycznego. Zmiany w T_core pomiędzy tubami przepływu reprezentują zmiany potencjału elektrycznego φ od rury do rury. Może to wskazywać, że międzyplanetarny potencjał φ (r) (Jockers, 1970 [49]; Lemons i Feldman, 1983 [64]; Lacombe et al., 2002 [61]; Salem et al., 2003 [96]; Lemaire, 2010 [63]) i jego wpływ na ewolucję jonów i elektronów w wietrze słonecznym (np. Lie-Svendsen i Leer, 2000 [69]; Meyer-Vernet et al., 2003 [81]) działa na zasadzie „tuba-po-tubie”.

Niniejsze opracowanie zostało zorganizowane w następujący sposób. W sekcji Dane opisano zbiory danych, które zostaną wykorzystane, wraz z algorytmem numerycznym zastosowanym w 1 AU do identyfikacji skoków w szeregach czasowych n_core i T_core. W Analizie Statystycznej Danych WIND w 1 AU opisano wyniki analizy statystycznej zbioru danych WIND w odległości 1 AU od Słońca, a w Badaniu Pomiarów Parker Solar Probe w Pobliżu Słońca opisano krótkie badanie pomiarów elektronowych Parker Solar Probe w odległości 0,13 AU. Podsumowanie i dyskusja podsumowuje wyniki badań i omawia wnioski z obserwowanej struktury elektronów rdzenia wiatru słonecznego.

DANE

Do zbadania struktury elektronowej wiatru słonecznego w odległości 1 AU użyto 12-sekundowych pomiarów momentów elektronów z instrumentu SWE (Ogilvie et al., 1995 [87]) na sondzie WIND w koordynacji z 3-sekundowymi pomiarami pola magnetycznego z instrumentu MFI (Lepping et al., 1995 [65]), również na WIND.

Analizie poddano pierwsze 120 dni roku 2005. Jest to ten sam przedział czasowy, który został wykorzystany do analizy struktury strahlu i stosunku liczbowo-gęstościowego alfa do protonów w wietrze słonecznym (Borovsky, 2020a [16]). Jest to przedział czasowy w fazie schyłkowej cyklu słonecznego, który zawiera dobrą mieszankę różnych typów plazmy pochodzącej ze Słońca z bardzo małą ilością wstrząsów międzyplanetarnych, mogących mylić kategoryzację typów plazmy wiatru słonecznego. Według schematu kategoryzacji wiatru słonecznego w 1 AU Xu i Borovsky’ego (2015) [113], ten 120-dniowy przedział czasowy zawierał, według ułamka czasu, 40.2% plazmy pochodzącej z dziury koronalnej, 30.0% plazmy pochodzącej z pasa strumieniowego, 14.5% plazmy z regionu sektora odwracania oraz 15.4% plazmy wyrzutowej. Jest to różnorodność, która reprezentuje uśrednioną dla cyklu słonecznego różnorodność typów plazmy widzianych w 1 AU, z naciskiem na plazmę pochodzącą z dziur koronalnych. Zobaczymy, że ten przedział daje tysiące zdarzeń do analizy statystycznej.

W danych serii czasowej WIND zastosowano algorytm numeryczny do zlokalizowania skoków (przesunięć) w wielkościach gęstości liczby elektronów rdzenia n_core i temperatury elektronów rdzenia T_core, które są większe niż poziom szumu w danych. Skoki te przyjęto jako przestrzenne granice w gęstości i w temperaturze elektronów. Dla każdego podejrzanego skoku czasowego badane są cztery punkty danych przed skokiem i cztery punkty danych po skoku. Aby skok był prawidłowy, 1) maksymalna wartość czterech punktów danych po jednej stronie skoku musi być mniejsza niż minimalna wartość czterech punktów danych po drugiej stronie skoku. Dalej, 2) zanim skok zostanie zaakceptowany, musi zostać przekroczona minimalna wartość przesunięcia: wartość bezwzględna zmiany średniej logarytmicznej czterech punktów przed skokiem od średniej logarytmicznej czterech punktów po skoku musi przekroczyć wartość progową Q. Przy zapisie, że „wartość” punktu danych v przed skokiem to v_iprzed, a wartość punktu danych po skoku to v_ipo, ten drugi warunek zapisujemy dla dwóch zbiorów czterech punktów

, gdzie przy sumowaniu czterech logarytmów wykorzystano log (A) + log (B) = log (AB). Dla skoków gęstości przyjmuje się Q = 0,0607 = log₁₀ (1,15) (co odpowiada większej niż 15% zmianie czteropunktowej średniej logarytmicznej w całym skoku), a dla skoków temperatury przyjmuje się Q = 0,414 = log₁₀ (1,1) (co odpowiada większej niż 10% zmianie czteropunktowej średniej logarytmicznej w całym skoku).

W ciągu 120 dni pomiarów serii czasowej WIND zidentyfikowano 3 436 skoków gęstości (średnio 28,6 skoków na dzień) oraz 1 648 skoków temperatury (13,7 skoków na dzień). Pięćset dwadzieścia sześć skoków zidentyfikowano zarówno jako skoki gęstości, jak i temperatury.

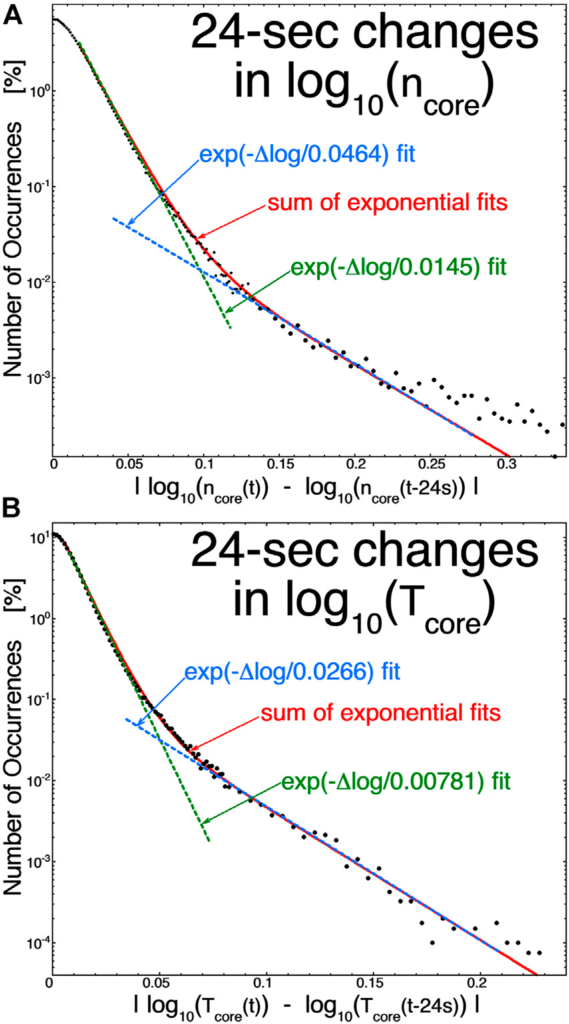
Ilustracja 1: Rozkłady występowania 24-sek. zmiany log₁₀(n_core) [panel (A)] i log₁₀(T_core) [panel (B)] zestawione są dla 120 dni pomiarów WIND w 1 AU.
Kategoryzując typ plazmy wiatru słonecznego w czasie każdego skoku n_core przy użyciu schematu kategoryzacji wiatru słonecznego w 1 AU Xu i Borovsky’ego (2015) [113], mamy 1382 skoków n_core w plazmie pochodzącej z dziury koronalnej, 607 skoków n_core w plazmie pochodzącej z pasa wstęgowego, 256 skoków n_core w plazmie z sektora zawracania i 1106 skoków n_core w plazmie z wyrzutowej. Podobnie jest 903 skoków T_core w plazmie pochodzącej z dziury koronalnej, 108 skoków T_core w plazmie pochodzącej z pasa wstęgowego, 29 skoków T_core w plazmie z obszaru sektora odwracania i 517 skoków T_core w plazmie wyrzutowej. Z powodu braku potwierdzonych pomiarów protonów wiatru słonecznego, niektóre z n_core i T_core nie mogły być skategoryzowane jako plazma.

W 0,13 AU, 14-sekundowe rytmiczne pomiary temperatury elektronów rdzenia z instrumentu elektronowego Parker Solar Probe SWEAP SPAN (Kasper et al., 2016 [50]; Whittlesey et al., 2020 [112]) używane są w połączeniu z pomiarami pola magnetycznego z magnetometrów fluxgate PSP FIELDS (Bale et al., 2016 [2]). Temperatury elektronów rdzenia uzyskano z dopasowania do zmierzonych funkcji rozkładu elektronów za pomocą procedury dopasowania opisanej w dodatku Halekas et al. (2020) [45].

Analiza statystyczna danych WIND w 1 AU

Ilustracja 1A przedstawia rozkład występowania 24-sekundowych zmian w log₁₀ (n_core) w pierwszych 120 dniach 2005 roku (czarne punkty), a Ilustracja 1B przedstawia analogiczne dane T_core. Użyto wartości bezwzględnych zmian. Oba rozkłady występowania na Ilustracji 1 wykazują dwa składniki: populację małych zmian, która jest dopasowana do stromego wykładnika (zielone przerywane krzywe) oraz drugą populację dużych zmian, która jest dopasowana do płytszego wykładnika (niebieskie przerywane krzywe). W obu wykresach suma dwóch dopasowań wykładniczych jest wykreślona jako czerwona krzywa. Podobne rozkłady dwuskładnikowe w wietrze słonecznym obserwujemy dla zmian natężenia pola magnetycznego B_mag, entropii właściwej protonu S_p, intensywności strumienia elektronów oraz stosunku liczby alfa do gęstości protonów α/p [por. ilustracja 3 Borovsky’ego (2008) [12]], wskazując na strukturę przestrzenną tych wielkości: wykazano, że składowe o większych wartościach w tych rozkładach dwuskładnikowych są związane z przecięciami arkuszy prądów. Poniżej zostanie pokazane, że populacje dużych zmian na rysunkach 1A,B są związane z przecięciami arkuszy prądów w wietrze słonecznym. Stąd, populacja dużych zmian na Ilustracji 1 jest zgodna z przecięciami granic n_core w wietrze słonecznym, a populacja dużych zmian na Ilustracji 1B jest zgodna z przecięciami granic T_core w wietrze słonecznym, przy czym granice te współwystępują z arkuszami prądu. Populacje małych zmian w obu panelach są zgodne z małymi fluktuacjami w n_core i T_core z dala od granic, lub z szumem w wartościach pomiarowych z dala od granic.

Jednym z pytań, które zostaną poruszone jest to, czy granice n_core i T_core w wietrze słonecznym mają tendencję do współwystępowania z arkuszami prądowymi struktury magnetycznej wiatru słonecznego.

Aby określić, czy istnieje związek pomiędzy granicami struktur n_core i T_core a silnymi arkuszami prądów w wietrze słonecznym, zbadano 30-sekundową zmianę kątową kierunku pola magnetycznego Δθ, gdy statek kosmiczny WIND przekracza te granice. Zapisując b(t) = B(t)/|B(t)|, 30-sekundowa zmiana kątowa kierunku pola magnetycznego w czasie t jest obliczana z szeregu czasowego wektora pola magnetycznego jako

Δθ = arcos (b(t + 15s)· b(t − 15s))

(2)

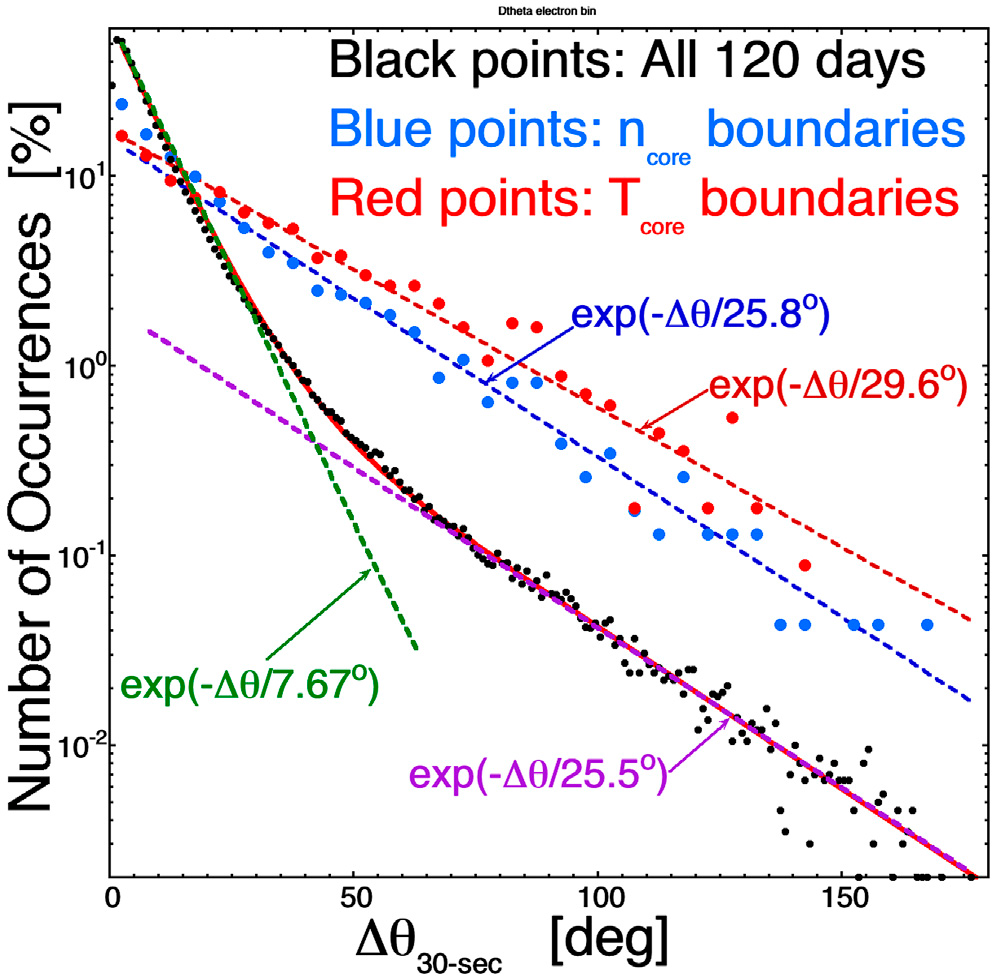
Na ilustracji 2 wykreślono niektóre rozkłady występowania 30-sekundowych zmian kierunku pola magnetycznego Δθ. Czarne punkty na określają rozkład wartości Δθ dla wszystkich czasów podczas pierwszych 120 dni 2005 roku, z wyłączeniem czasów, gdy sonda WIND znajdowała się w plazmie wyrzutowej. Zwróćmy uwagę na dwie składowe rozkładu Δθ w punkcie czarnym, składową o małym kącie dopasowaną przez exp(-Δθ/7,67°) (zielona przerywana krzywa) oraz składową o dużym kącie dopasowaną przez exp(-Δθ/25,5°) (fioletowa przerywana krzywa). Ciągła czerwona krzywa jest sumą dwóch dopasowań wykładniczych [Patrz także Rysunek 2 u Borovsky’ego (2008) [12] i Rysunek 6 Miao et al. (2011) [82] dla podobnych dwuskładnikowych rozkładów Δθ]. Część rozkładu o dużej Δθ została zinterpretowana jako reprezentująca przecięcia silnych arkuszy prądowych w wietrze słonecznym (Burlaga i Ness, 1969 [23]; Knetter et al., 2004 [60]; Borovsky, 2008 [12]) (ściany tub przepływu pomiędzy jedną tubą a jej sąsiadem), a część rozkładu o małej Δθ została przyjęta jako reprezentująca małe fluktuacje pola magnetycznego we wnętrzu tuby przepływu. Oczekuje się, że duża składowa Δθ rozkładu czarnych punktów rozciąga się do mniejszych wartości Δθ poniżej punktu załamania krzywej: czerwona ciągła krzywa dopasowana do czarnych punktów jest sumą dwóch dopasowań wykładniczych. W spaghetti rurek strumienia magnetycznego kąt kierunku pola magnetycznego w jednej tubie z vs. sąsiedniej jest funkcją odległości wzdłuż tuby, tak że czasami wartość Δθ między tubami jest duża, a czasami mała, nawet zerowa. Stąd użycie kryterium dużego Δθ do znalezienia ścian tub strumienia nie pozwoli zlokalizować niektórych ścian (ściany czasami można zlokalizować poprzez inne własności, np. skoki własności plazmy). Średnia wartość Δθ dla exp (-Δθ/25,5°) wynosi <Δθ > = 25,5°, a średnia wartość Δθ dla całego rozkładu czarnych punktów (suma dwóch dopasowań wykładniczych) wynosi <Δθ> = 10.2°. Niebieskie punkty na ilustracji 2 wykreślają rozkład 30-sekundowych wartości Δθ w czasie, gdy widoczne są skoki (granice) w n_core. Te niebieskie punkty danych są dopasowane funkcją wykładniczą exp(-Δθ/25,8°) (ciemno-niebieska przerywana krzywa), która jest podobna do exp(-Δθ/25.5o) dopasowania dużej-Δθ dla przejść arkusza prądowego dla rozkładu czarnych punktów na ilustracji 2. Zauważmy, że ten rozkład niebieskich punktów rozciąga się w dół do małych wartości Δθ, co prawdopodobnie reprezentuje skrzyżowania pomiędzy tubami strumienia, które są lokalnie prawie wyrównane w punkcie skrzyżowania. Stąd wartości Δθ, widziane w czasie przekraczania granic n_core w wietrze słonecznym (niebieskie punkty), są zgodne z przecięciami silnych arkuszy prądowych w wietrze słonecznym. Czerwone punkty na ilustracji 2 wykreślają rozkład 30-seundowych wartości Δθ w czasie, gdy widoczne są skoki (granice) w T_core. Te punkty danych są dopasowane funkcją wykładniczą exp(-Δθ/29,6°) (ciemno-czerwona przerywana krzywa), która jest również podobna do exp(-Δθ/25,5°) dopasowania przejść przez arkusze prądowe dla rozkładu czarnych punktów na ilustracji 2. I zauważmy ponownie, że ten rozkład czerwonych punktów rozciąga się w dół do małych wartości Δθ. Stąd wartości Δθ, widziane w momentach przekraczania granic T_core w wietrze słonecznym, są zgodne z przecięciami silnych arkuszy prądowych w wietrze słonecznym (uwaga, w zbiorze granic n_core i T_core, te dwie granice często współwystępują).

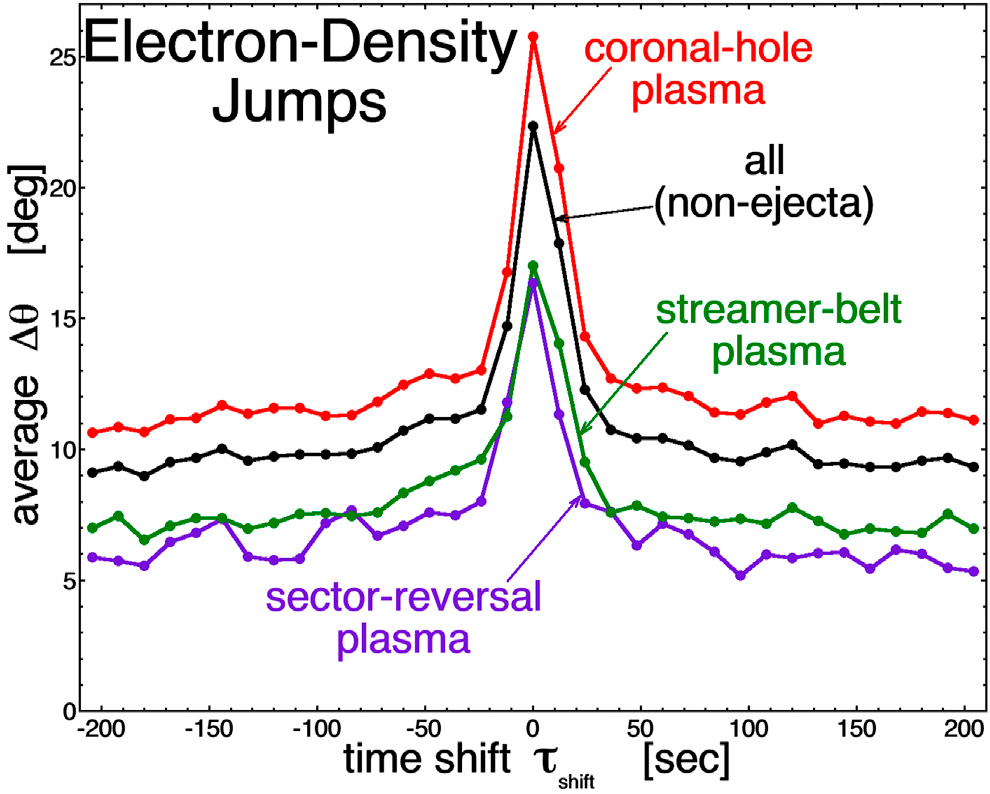
Na ilustracji 3 wykreślona jest nałożona epokowa średnia wartość zmiany kierunku pola magnetycznego Δθ w funkcji czasu dla zidentyfikowanych skoków wartości n_core. Przesunięcie czasowe τ_shift = 0 na wykresie oznacza, że 30-sekundowa zmiana Δθ w kierunku pola magnetycznego jest wyśrodkowana w czasach skoków wartości n_core, a przesunięcia czasowe różne od 0 mają 30-sekundową zmianę Δθ wyśrodkowaną w czasie odległym o τ_shift od skoków wartości n_core. Poszczególne krzywe na ilustracji 3 odnoszą się do zbiorów rozpoznanych granic n_core w różnych typach plazmy wiatru słonecznego, wyznaczonych za pomocą schematu kategoryzacji plazmy Xu i Borovsky’ego (2015) [113]. Z ilustracji 3 wyłączone są granice n_core występujące w plazmie wyrzutowej; plazma wyrzutowa często charakteryzuje się płynnie zmieniającym się kierunkiem pola magnetycznego (Klein i Burlaga, 1982 [58]; Cane i Richardson, 2003 [25]), niskim poziomem fluktuacji pola (Lepping et al., 2005 [66]; Borovsky et al., 2019 [10]) oraz brakiem silnych arkuszy prądowych (Borovsky, 2008 [12]; Borovsky, 2012a [14]). Zauważmy na ilustracji 3, że średnia wartość Δθ jest znacznie większa w momencie przekraczania granic (τ_shift = 0) niż z dala od granic (τ_shift ≠ 0): wskazuje to, że granice n_core w wietrze słonecznym mają tendencję do współwystąpień z silnymi arkuszami prądowymi, co zostało również wskazane na ilustracji 2. Wartości Δθ przy τ_shift = 0 na ilustracji 3 są zgodne ze średnią wartością <Δθ> = 25,5° dla części exp(-Δθ/25,5°) rozkładu czarnych punktów na ilustracji 2. Wartości Δθ z dala od τ_shift = 0 na ilustracji 3 są zgodne z <Δθ> = 10,2°, ustalonym dla całkowitego rozkładu czarnych punktów (arkusze i nie arkusze) na ilustracji 2. Stąd zmiany w n_core mają tendencję do występowania przy przejściu z jednej tuby strumienia magnetycznego do innej tuby. Zwróćmy uwagę na ilustracji 3 na systematycznie różniącą się amplitudę Δθ w różnych kategoriach plazmy wiatru słonecznego (na różnokolorowych krzywych); te systematyczne różnice w „kącie luzu” pola magnetycznego w różnych typach plazmy zostały zbadane we wcześniejszych badaniach [por. ilustrację 11 Borovsky’ego i Dentona (2010) [7] lub ilustrację 8a Borovsky’ego et al. (2019) [10]].

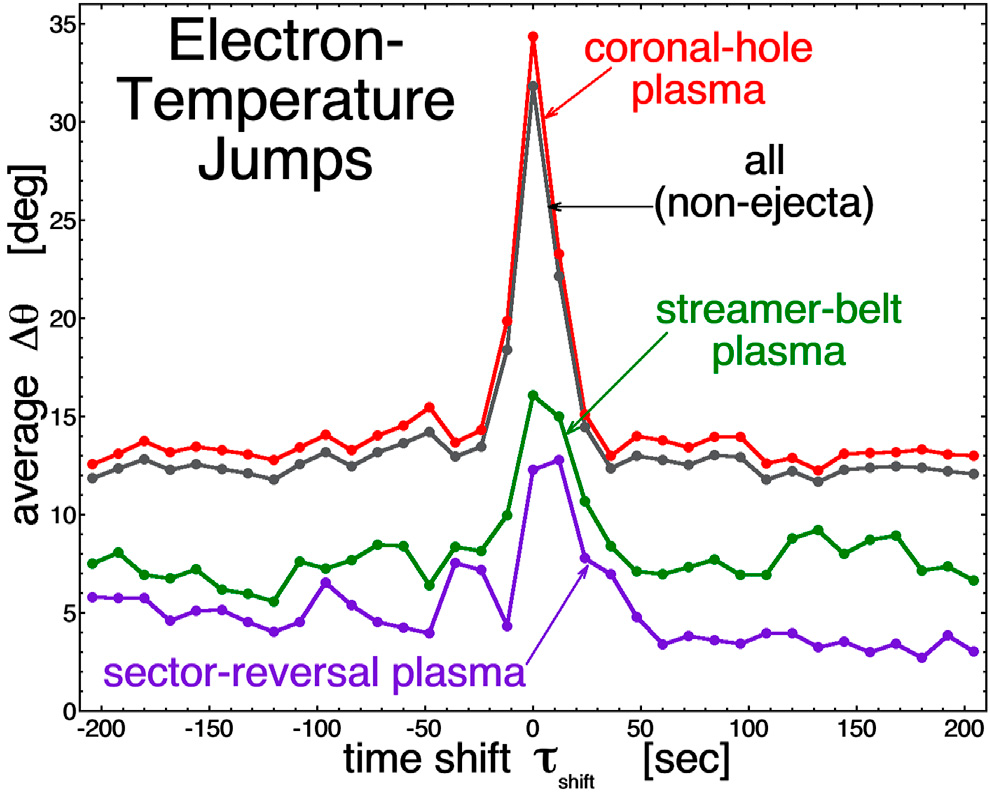
Podobnie, na ilustracji 4, nałożona średnia epokowa Δθ wykreślona jest w funkcji czasu od zidentyfikowanych skoków wartości T_core, przy czym τ_shift = 0 oznacza, że 30-sekundowa zmiana Δθ w kierunku pola magnetycznego jest wyśrodkowana w czasach skoków T_core. Poszczególne krzywe na Ilustracji 4 odnoszą się do zbiorów zidentyfikowanych granic T_core w różnych typach plazmy wiatru słonecznego. Ponownie, wyłączone są granice T_core występujące w plazmie wyrzutowej. Na Ilustracji 4 średnia wartość Δθ jest znacznie większa w momencie przekraczania granicy T_core (τ_shift = 0) niż z dala od granicy T_core (τ_shift ≠ 0). Wartości Δθ w τ_shift = 0 na Ilustracji 4 są ponownie zgodne ze średnią wartością <Δθ> = 25,5° dla exp(-Δθ/25,5°) części rozkładu czarnych punktów na Ilustracji 2, a wartości Δθ z dala od τ_shift = 0 na Ilustracji 4 są ponownie zgodne z wartością <Δθ> = 10,2°, znalezioną dla całkowitego rozkładu czarnych punktów (arkusze i nie arkusze) na Ilustracji 2. Ilustracja 4 wskazuje, że granice T_core w wietrze słonecznym mają tendencję do współwystąpień z silnymi arkuszami prądów w wietrze słonecznym, co zostało również wskazane na Ilustracji 2. W związku z tym zmiany T_core występują przy przejściu z jednej tuby strumienia magnetycznego do innej tuby.

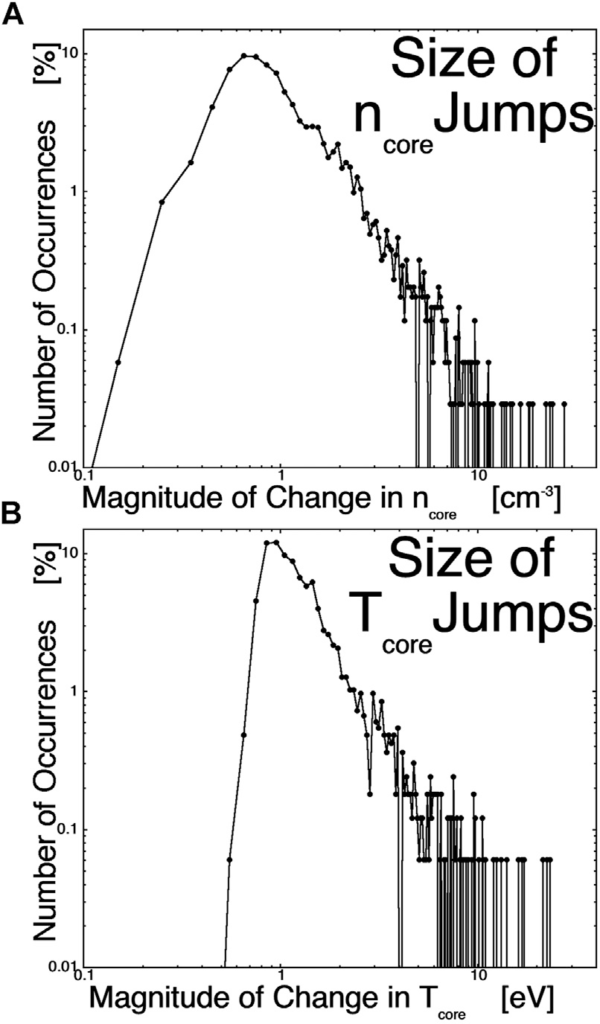
Wracając do dwuskładnikowego rozkładu Δθ z Ilustracji 2, można zadać pytanie: Jaki ułamek przejść przez arkusz prądowy nie ma wartości Δθ wystarczająco dużych, aby można je było wykryć z szumu rozkładu małych Δθ? Dla składowej małych Δθ rozkładu czarnych punktów z Ilustracji 2, która jest dopasowana przez exp (-Δθ/7.67°), 95% punktów w tym rozkładzie ma Δθ < 23,0°. Wartość Δθ dla granicy elektronów większa niż 23,0° prawdopodobnie wyróżniałaby się w szeregu czasowym od wartości tła. Zakładając, że rozkład exp(-Δθ/25,5°) przejść przez arkusz prądowy rozciąga się w dół do Δθ = 0° (tak jak rozkłady czerwonych punktów i niebieskich punktów na Ilustracji 2), to 41% punktów w rozkładzie exp(-Δθ/25,5°) ma Δθ > 23,0°. Stąd można się spodziewać, że około połowa (41%) granic zimnych elektronów będzie indywidualnie identyfikowana jako przejścia przez arkusz prądowy, a około połowa (59%) będzie miała wartości Δθ zbyt małe, aby jednoznacznie zidentyfikować je jako przejścia przez arkusz prądowy, choć prawdopodobnie nimi są.

Na Ilustracji 5 zbadano amplitudy zidentyfikowanych skoków w n_core (Ilustracja 5A) i zidentyfikowanych skoków w T_core (Ilustracja 5B). Tutaj wykreślone są rozkłady występowania amplitudy skoków, gdzie amplitudy są zestawione z liniowymi wartościami podwójnymi, ale wykreślone są logarytmicznie. Amplituda skoku jest tutaj mierzona przez wartość bezwzględną różnicy między średnią wartością czterech punktów danych przed skokiem i średnią wartością czterech punktów danych po skoku. Jak widać na Ilustracji 5A, typowe wartości skoku n_core wynoszą ∼1 cm^-3, przy czym nie są rzadkością wartości tak duże jak 5 cm^-3. Rysunek 5B przedstawia rozkład amplitudy skoków dla T_core: typowe wartości to ∼1 eV, ale nie są rzadkością wartości rzędu 5 eV lub więcej.

Badanie pomiarów z Parker Solar Probe w pobliżu Słońca

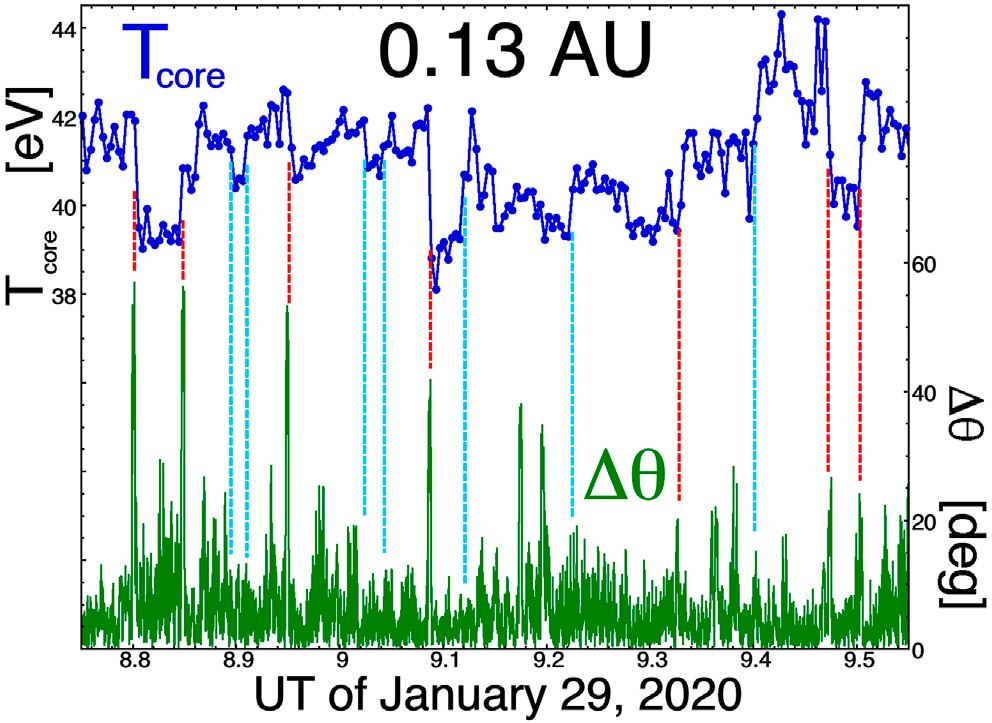
Krótkie, niestatystyczne badanie dotyczy pomiarów elektronów rdzenia przez sondę Parker Solar Probe podczas bliskiego spotkania ze Słońcem w styczniu 2020 roku. Na ilustracjach 6 i 7 wykreślono dwa szeregi czasowe temperatury T_core populacji elektronów rdzenia (niebieski) wraz z 10-sekundową zmianą kierunku pola magnetycznego Δθ (zielony). Skoki wartości T_core są zaznaczone pionowymi odcinkami linii przerywanej: skoki te są identyfikowane poprzez wizualną inspekcję szeregów czasowych i nie są one identyfikowane za pomocą 8-punktowego algorytmu numerycznego [wyrażenie (1)], który został użyty do identyfikacji skoków w szeregach czasowych WIND w 1 AU. Skoki wartości T_core, które są związane z silnymi zmianami Δθ w kierunku pola, oznaczono czerwonymi, pionowymi przerywanymi segmentami linii, a skoki wartości T_core, które nie są związane z silnymi zmianami Δθ w kierunku pola, oznaczono jasnoniebieskimi, pionowymi przerywanymi segmentami linii. Ilustracja 6 przedstawia 48 minut pomiarów w 0,13 AU w dniu 29 stycznia 2020 roku, a ilustracja 7 przedstawia 15,6 minut pomiarów w 0,13 AU w dniu 30 stycznia 2020 roku. Na ilustracji 6 sześć skoków w T_core jest oznaczonych czerwonymi, pionowymi odcinkami wskazującymi, że są one związane z lokalnymi dużymi wartościami Δθ, tzn. te przesunięcia wartości T_core są związane z przecięciami silnych arkuszy prądowych w wietrze słonecznym. Na ilustracji 6 sześć skoków wartości T_core zaznaczono jasnoniebieskimi, pionowymi odcinkami, wskazującymi, że nie są one związane z przecięciami arkuszy prądów w wietrze słonecznym wystarczająco silnymi, aby mieć wartości Δθ większe niż wartości tła. (Tak jest również w przypadku skoków T_core w 1 AU, co omówiono w Analizie Statystycznej Danych z WIND w 1 AU i co pokazuje rozkład czerwonych punktów na ilustracji 2, gdzie rozkład wartości Δθ dla skoków T_core rozciąga się w dół do niskich wartości Δθ). Te skoki T_core o niskim Δθ można by zinterpretować jako skoki związane z tubami strumienia, które są lokalnie bliskie równoległości, gdy statek kosmiczny przechodzi z jednej tuby do drugiej. Na ilustracji 7 wszystkie sześć zaobserwowanych przesunięć w T_core jest związanych z silnymi skrzyżowaniami arkuszy prądowych (czerwone odcinki linii przerywanej). Zwróćmy uwagę na wielkość wartości Δθ w czasie skoków T_core, często pokazujących rotację pola magnetycznego o ponad 90° w poprzek arkuszy prądowych. Badanie dwóch szeregów czasowych na ilustracjach 6 i 7 wskazuje, że przy 0,13 AU struktura przestrzenna temperatury elektronów rdzenia T_core jest związana ze strukturą tub strumienia magnetycznego, podobnie jak przy 1 AU.

Zauważmy, że żadna ze zmian T_core, zaznaczonych na ilustracjach 6 i 7, nie jest związana z magnetycznym przełączaniem zwrotnym (fałdowaniem lub odwracaniem pola), które czasami są powszechne w zestawie danych Parker Solar Probe (Dudok de Wit et al., 2020 [34]; Macneil et al., 2020 [70]). Najbliższe jest zdarzenie w 4,203 UT na ilustracji 7, gdzie pole magnetyczne dokonuje przejścia z orientacji poprzecznej do niemal radialnej.

Typowe zmiany wartości T_core w skokach zaznaczonych na Il. 6, 7 wynoszą 2-3 eV.

Podsumowanie i dyskusja

Analiza statystyczna 120-dniowych pomiarów wiatru słonecznego w odległości 1 AU pokazuje, że struktura gęstości i struktura temperatury elektronów rdzenia wiatru słonecznego są związane ze strukturą tub strumienia magnetycznego wiatru słonecznego; w tej strukturze gęstość liczbowa n_core i temperatura T_core populacji elektronów rdzenia mają tendencję do skokowych zmian wartości przy przechodzeniu pomiędzy tubami strumienia. Badanie pomiarów T_core na wysokości 0,13 AU pokazuje te same cechy związane ze strukturą magnetyczną, ze skokami T_core związanymi z przejściami przez arkusze prądowe.

Związek gęstości liczbowej elektronów n_core z tubami strumienia magnetycznego nie jest zaskoczeniem w świetle rozważań o quasi-neutralności, gdyż wiadomo, że struktura gęstości liczbowej protonów w wietrze słonecznym odzwierciedla strukturę magnetyczną (Borovsky, 2012b [15]; Borovsky, 2020b [17]). Bardziej interesujące są zmiany T_core, które są związane ze strukturą tub smagnetycznych. Jeśli lokalna wartość T_core reprezentuje pomiar lokalnego potencjału elektrycznego φ, to T_core zmieniający się od tuby do tuby oznacza, że φ też zmienia się od tuby do tuby. Jeśli φ(r) jest (jak w modelu egzosfery) określona przez ewolucję jonów i elektronów wiatru słonecznego z dala od Słońca, wtedy zmiany φ od rury do rury mogą oznaczać, że modele egzosfery stosują się do poszczególnych tub, tj. że ewolucja wiatru słonecznego jest do pewnego stopnia niezależna w każdej tubie. Nie ma powodu, by twierdzić, że różniące się tuby strumienia nie powinny działać niezależnie. Na wysokości 1 AU widać, że intensywność strumienia elektronów może być różna w zależności od rury strumienia (Borovsky, 2021 [20]): ta zmienność strumienia wskazuje, że różne rury strumienia na wysokości 1 AU są połączone z różnymi strukturami w koronie (Gosling et al., 2004a [38], b [39]; Borovsky, 2021 [20]). Różnice w połączeniu z koroną mogą skutkować niezależnymi scenariuszami egzosferycznymi w różnych tubach strumienia.

Jeśli plazma wiatru słonecznego jest domieszką otwartych tub strumienia i innych struktur magnetycznych (np. rysunek 24C w Khabarova et al., 2021 [55]) to obraz modelu egzosfery jest bardziej skomplikowany. Potrzebne są dalsze badania pomiarów pola i elektronów rdzenia w odległości 1 AU, połączone z pomiarami intensywności strahlu, aby ocenić łączność magnetyczną ze Słońcem (Borovsky, 2021 [20]). Interpretacja T_core jako wskaźnika lokalnego potencjału elektrycznego φ w każdej zamkniętej strukturze magnetycznej (np. Feldman et al., 1975 [36]; Boldyrev et al., 2020 [6]; Moncuquet et al., 2020 [84]) może nie być już możliwa.

Zarówno w 1 jak i 0,13 AU ułamkowa zmienność T_core w typowym skoku wynosi około 10%, choć sporadycznie można znaleźć znacznie większe skoki (kilkadziesiąt procent). Wskazuje to na zmienność potencjału międzyplanetarnego o około 10% pomiędzy tubami, choć nie każde przejście rura-ściana wykazuje skok T_core.

Przy 1 AU typowe zmiany T_core na ścianach tub strumienia wynoszą ∼1 eV, choć można znaleźć większe potencjały. Oznacza to zmianę potencjału elektrycznego o ∼1 V na granicy między sąsiednimi rurami strumienia. Jeśli w 1 AU arkusz prądu (ściana rury strumieniowej) ma grubość 1000 km (np. Siscoe et al., 1968 [100]; Vasquez et al., 2007 [106]), a zmiana potencjału wynosi 1 V, to pole elektryczne tej zmiany potencjału wynosi E = 1 × 10^-6 V/m. Dla natężenia pola magnetycznego 5 nT odpowiada to prędkości dryfu E × B równej 0,2 km/s [Zauważmy, że jeśli potencjał jest kilka razy większy od temperatury elektronów rdzenia (por. Maksimovic et al., 1997 [71]), to te wartości pola elektrycznego i prędkości dryfu są kilka razy większe].

W przyszłości potrzebna jest analiza statystyczna zmian T_core w danych z Parker Solar Probe, uwzględniająca rodzaje obserwowanej plazmy oraz szybki ruch wzdłużny statku kosmicznego. W szczególności interesujące będzie, gdy w przyszłości dojdzie do zbliżenia do Słońca i będzie można zbadać zmiany międzyplanetarnego potencjału elektrycznego, gdzie przewiduje się, że potencjały będą wyższe blisko Słońca.

Dostępność danych

W niniejszym opracowaniu analizie poddano publicznie dostępne zbiory danych. Dane te można znaleźć tutaj: https://cdaweb.gsfc.nasa.gov/index.html/.

Wkład autorów

JB zainicjował ten projekt, przeprowadził analizę danych i napisał wstępny projekt manuskryptu. JH i PW przygotowali dane z sondy Solar Solar Probe Data i przyczynili się do powstania ostatecznej wersji manuskryptu.

Finansowanie

Praca ta była wspierana przez program NSF SHINE poprzez grant nr AGS-1723416, przez NASA Heliophysics Guest Investigator Program poprzez grant NNX17AB71G, przez NSF GEM Program poprzez grant nr AGS-2027569 oraz przez program NASA Heliophysics LWS poprzez grant NNX16AB75G. JH i PW byli wspierani przez PSP SWEAP kontraktem NNN06AA01C.

Uznania

Autorzy dziękują Stasowi Boldyrevowi i Vadimowi Roytershteynure za pomocne rozmowy.

ODNOŚNIKI

1. Adhikari, L., Khabarova, O., Zank, G. P., and Zhao, L.-L. (2019). The Role of Magnetic Reconnection-Associated Processes in Local Particle Acceleration in the Solar Wind. ApJ 873, 72. doi:10.3847/1538-4357/ab05c6
2. Bale, S. D., Goetz, K., Harvey, P. R., Turin, P., Bonnell, J. W., de Wit, T. D., et al. (2016). The FIELDS Instrument Suite for Solar Probe Plus: Measuring the Coronal Plasma and Magnetic Field, Plasma Waves and Turbulence, and Radio Signatures of Solar Transients. Space Sci. Rev. 204, 49–82. doi:10.1007/s11214-016-0244-5
3. Bartley, W. C., Bukata, R. P., McCracken, K. G., and Rao, U. R. (1966). Anisotropic Cosmic Radiation Fluxes of Solar Origin. J. Geophys. Res. 71, 3297–3304. doi:10.1029/jz071i013p03297
4. Birch, M. J., and Hargreaves, J. K. (2020a). Quasi-periodic Ripples in High-Latitude Electron Content, the Geomagnetic Field, and the Solar Wind. Nat. Scienific Rep10, 1313. doi:10.1038/s41598-019-57201-4
5. Birch, M. J., and Hargreaves, J. K. (2020b). Quasi-periodic Ripples in the Heliosphere from 1 to 40 AU. Adv. Space Res. 67, 678.
6. Boldyrev, S., Forest, C., and Egedal, J. (2020). Electron Temperature of the Solar Wind. Proc. Natl. Acad. Sci. USA 117, 9232–9240. doi:10.1073/pnas.1917905117
7. Borovsky, J. E., and Denton, M. H. (2010). Solar Wind Turbulence and Shear: A Superposed-Epoch Analysis of Corotating Interaction Regions at 1 AU. J. Geophys. Res. 115, A10101. doi:10.1029/2009ja014966
8. Borovsky, J. E., and Denton, M. H. (2016). The Trailing Edges of High-Speed Streams at 1 AU. J. Geophys. Res. Space Phys. 121, 6107–6140. doi:10.1002/2016ja022863
9. Borovsky, J. E., and Steinberg, J. T. (2014). No Evidence for the Localized Heating of Solar Wind Protons at Intense Velocity Shear Zones. J. Geophys. Res. Space Phys. 119, 1455–1462. doi:10.1002/2013ja019746
10. Borovsky, J. E., Denton, M. H., and Smith, C. W. (2019). Some Properties of the Solar-Wind Turbulence at 1 AU Statistically Examined in the Different Types of Solar-Wind Plasma. J. Geophys. Res. 124, 2406. doi:10.1029/2019JA026580
11. Borovsky, J. E. (2006). The Eddy Viscosity and Flow Properties of the Solar Wind: CIRs, CME Sheaths, and Solar-Wind/magnetosphere Coupling. Phys. Plasmas 13, 056505. doi:10.1063/1.2200308
12. Borovsky, J. E. (2008). Flux Tube Texture of the Solar Wind: Strands of the Magnetic Carpet at 1 AU?. J. Geophys. Res. 113, A08110. doi:10.1029/2007ja012684
13. Borovsky, J. E. (2010). On the Variations of the Solar Wind Magnetic Field about the Parker Spiral Direction. J. Geophys. Res. 115, A09101. doi:10.1029/2009ja015040
14. Borovsky, J. E. (2012a). The Velocity and Magnetic Field Fluctuations of the Solar Wind at 1 AU: Statistical Analysis of Fourier Spectra and Correlations with Plasma Properties. J. Geophys. Res. 117, A05104. doi:10.1029/2011ja017499
15. Borovsky, J. E. (2012b). Looking for Evidence of Mixing in the Solar Wind from 0.31 to 0.98 AU. J. Geophys. Res. 117, A06107. doi:10.1029/2012ja017525
16. Borovsky, J. E. (2020a). The Magnetic Structure of the Solar Wind: Ionic Composition and the Electron Strahl. Geophys. Res. Lett. 47, e2019GL084586. doi:10.1029/2019gl084586
17. Borovsky, J. E. (2020b). Plasma and Magnetic-Field Structure of the Solar Wind at Inertial-Range Scale Sizes Discerned from Statistical Examinations of the Time-Series Measurements. Front. Astron. Space Sci. 7, 20. doi:10.3389/fspas.2020.00020
18. Borovsky, J. E. (2020c). On the Motion of the Heliospheric Magnetic Structure through the Solar Wind Plasma. J. Geophys. Res. 125, e2019JA027377. doi:10.1029/2019ja027377
19. Borovsky, J. E. (2020d). Compression of the Heliospheric Magnetic Structure by Interplanetary Shocks: Is the Structure at 1 AU a Manifestation of Solar-Wind Turbulence or Is it Fossil Structure from the Sun?. Front. Astron. Space Sci. 7, 582546. doi:10.3389/fspas.2020.582564
20. Borovsky, J. E. (2021). Exploring the Properties of the Electron Strahl at 1 AU as an Indicator of the Quality of the Magnetic Connection between the Earth and the Sun. Front. Astron. Space Sci. 8, 646443. doi:10.3389/fspas.2021.646443
21. Bruno, R., Carbone, V., Veltri, P., Pietropaolo, E., and Bavassano, B. (2001). Identifying Intermittency Events in the Solar Wind. Planet. Space Sci. 49, 1201–1210. doi:10.1016/s0032-0633(01)00061-7
22. Burkholder, B. L., Otto, A., Delamere, P. A., and Borovsky, J. E. (2019). Magnetic Connectivity in the corona as a Source of Structure in the Solar Wind. J. Geophys. Res. Space Phys. 124, 32–49. doi:10.1029/2018ja026132
23. Burlaga, L. F., and Ness, N. F. (1969). Tangential Discontinuities in the Solar Wind. Sol. Phys. 9, 467–477. doi:10.1007/bf02391672
24. Burlaga, L. F. (1969). Directional Discontinuities in the Interplanetary Magnetic Field. Sol. Phys. 7, 54–71. doi:10.1007/bf00148406
25. Cane, H. V., and Richardson, I. V. (2003). Interplanetary Coronal Mass Ejections in the Near-Earth Solar Wind during 1996-2002. J. Geophys. Res. 108, 1156. doi:10.1029/2002ja009817
26. Close, R. M., Parnell, C. E., MacKay, D. H., and Priest, E. R. (2003). Statistical Flux Tube Properties of 3D Magnetic Carpet fields. Solar Phys. 212, 251–275. doi:10.1023/a:1022961913168
27. Close, R. M., Parnell, C. E., and Priest, E. R. (2005). Separators in 3D Quiet-Sun Magnetic fields. Solar Phys. 225, 21. doi:10.1023/A:1022961913168
28. Colburn, D. S., and Sonett, C. P. (1966). Discontinuities in the Solar Wind. Space Sci. Rev. 5, 439. doi:10.1007/bf00240575
29. DeForest, C. E., Howard, R. A., Velli, M., Viall, N., and Vourlidas, A. (2018). The Highly Structured Outer Solar corona. ApJ 862, 18. doi:10.3847/1538-4357/aac8e3
30. Di Matteo, S., Viall, N. M., Kepko, L., Wallace, S., Arge, C. N., and MacNeice, P. (2019). Helios Observations of Quasiperiodic Density Structures in the Slow Solar Wind at 0.3, 0.4, and 0.6 AU. J. Geophys. Res. Space Phys. 124, 837–860. doi:10.1029/2018ja026182
31. Dmitruk, P., Matthaeus, W. H., and Seenu, N. (2004). Test Particle Energization by Current Sheets and Nonuniform fields in Magnetohydrodynamic Turbulence. ApJ 617, 667–679. doi:10.1086/425301
32. Dobrowolny, M., Mangeney, A., and Veltri, P. (1980). Fully Developed Anisotropic Hydromagnetic Turbulence in Interplanetary Space. Phys. Rev. Lett. 45, 144–147. doi:10.1103/physrevlett.45.144
33. Doss, C. E., Komar, C. M., Cassak, P. A., Wilder, F. D., Eriksson, S., and Drake, J. F. (2015). Asymmetric Magnetic Reconnection with a Flow Shear and Applications to the Magnetopause. J. Geophys. Res. Space Phys. 120, 7748–7763. doi:10.1002/2015ja021489
34. Dudok de Wit, T., Krasnoselskikh, V. V., Bale, S. D., Bonnell, J. W., Bowen, T. A., Chen, C. H. K., et al. (2020). Switchbacks in the Near-Sun Magnetic Field: Long Memory and Impact on the Turbulence cascade. ApJS 246, 39. doi:10.3847/1538-4365/ab5853
35. Eselevich, V. G. (2019). Diamagnetic Structures as a Basis of Quasi-Stationary Slow Solar Wind. Solar-terr. Phys. 5 (3), 29.
36. Feldman, W. C., Asbridge, J. R., Bame, S. J., Montgomery, M. D., and Gary, S. P. (1975). Solar Wind Electrons. J. Geophys. Res. 80, 4181–4196. doi:10.1029/ja080i031p04181
37. Feldman, W. C., Asbridge, J. R., Bame, S. J., Gosling, J. T., and Lemons, D. S. (1978). Characteristic Electron Variations across Simple High-Speed Solar Wind Streams. J. Geophys. Res. 83, 5285. doi:10.1029/ja083ia11p05285
38. Gosling, J. T., de Koning, C. A., Skoug, R. M., Steinberg, J. T., and McComas, D. J. (2004a). Dispersionless Modulations in Low-Energy Solar Electron Bursts and Discontinuous Changes in the Solar Wind Electron Strahl. J. Geophys. Res. 109, A05102. doi:10.1029/2003ja010338
39. Gosling, J. T., Skoug, R. M., McComas, D. J., and Mazur, J. E. (2004b). Correlated Dispersionless Structure in Suprathermal Electrons and Solar Energetic Ions in the Solar Wind. ApJ 614, 412–419. doi:10.1086/423368
40. Gosling, J. T., Skoug, R. M., McComas, D. J., and Smith, C. W. (2005). Direct Evidence for Magnetic Reconnection in the Solar Wind Near 1 AU. J. Geophys. Res. 110, A01107. doi:10.1029/2004ja010809
41. Gosling, J. T. (2012). Magnetic Reconnection in the Solar Wind. Space Sci. Rev. 172, 187–200. doi:10.1007/s11214-011-9747-2
42. Greco, A., Chuychai, P., Matthaeus, W. H., Servidio, S., and Dmitruk, P. (2008). Intermittent MHD Structures and Classical Discontinuities. Geophys. Res. Lett. 35, L19111. doi:10.1029/2008gl035454
43. Greco, A., Matthaeus, W. H., Servidio, S., Dmitruk, P., Wan, M., Oughton, S., et al. (2010). Statistical Propertie of Solar Wind Discontinuities, Intermittent Turbulence, and Rapid Emergence of Non-gaussian Distribution. AIP Conf. Proc. 1216, 202. doi:10.1063/1.3395836
44. Greco, A., Perri, S., Servidio, S., Yordanova, E., and Veltri, P. (2016). The Complex Structure of Magnetic Field Discontinuities in the Turbulent Solar Wind. ApJ 823, L39. doi:10.3847/2041-8205/823/2/l39
45. Halekas, J. S., Whittlesey, P., Larson, D. E., McGinnis, D., Maksimovic, M., Berthomier, M., et al. (2020). Electrons in the Young Solar Wind: First Results from the Parker Solar Probe. ApJS 246, 22. doi:10.3847/1538-4365/ab4cec
46. Hannum, D., Bateman, G., Kinsey, J., Kritz, A. H., Onjun, T., and Pankin, A. (2001). Comparison of High-Mode Predictive Simulations Using Mixed Bohm/gyro-Bohm and Multi-Mode (MMM95) Transport Models. Phys. Plasmas 8, 964–974. doi:10.1063/1.1338534
47. Hesse, M., Birn, J., and Kuznetsova, M. (2001). Collisionless Magnetic Reconnection: Electron Processes and Transport Modeling. J. Geophys. Res. 106, 3721–3735. doi:10.1029/1999ja001002
48. Huang, C., Yan, Y., Li, G., Deng, Y., and Tan, B. (2014). Tracking Back the Solar Wind to its Photospheric Footpoints from Wind Observations – A Statistical Study. Sol. Phys. 289, 3109–3119. doi:10.1007/s11207-014-0508-8
49. Jockers, K. (1970). Solar Wind Models Based on Exospheric Theory. Astron. Astrophys. 6, 219.
50. Kasper, J. C., Abiad, R., Austin, G., Balat-Pichelin, M., Bale, S. D., Belcher, J. W., et al. (2016). Solar Wind Electrons Alphas and Protons (SWEAP) Investigation: Design of the Solar Wind and Coronal Plasma Instrument Suite for Solar Probe Plus. Space Sci. Rev. 204, 131–186. doi:10.1007/s11214-015-0206-3
51. Kepko, L., and Spence, H. E. (2003). Observations of Discrete, Global Magnetospheric Oscillations Directly Driven by Solar Wind Density Variations. J. Geophys. Res. 108, 1257. doi:10.1029/2002ja009676
52. Kepko, L., and Viall, N. M. (2019). The Source, Significance, and Magnetospheric Impact of Periodic Density Structures within Stream Interaction Regions. J. Geophys. Res. 124, 2019JA026962. doi:10.1029/2019ja026962
53. Kepko, L., Viall, N. M., Antiochos, S. K., Lepri, S. T., Kasper, J. C., and Weberg, M. (2016). Implications of L1 Observations for Slow Solar Wind Formation by Solar Reconnection. Geophys. Res. Lett. 43, 4089–4097. doi:10.1002/2016gl068607
54. Khabarova, O., Zharkova, V., Xia, Q., and Malandraki, O. E. (2020). Counterstreaming Strahls and Heat Flux Dropouts as Possible Signatures of Local Particle Acceleration in the Solar Wind. ApJ 894, L12. doi:10.3847/2041-8213/ab8cb8
55. Khabarova, O., Malandraki, O., malova, H., Kislov, R., Greco, A., Bruno, R., et al.(2021). Current Sheets, Plasmoids and Flux Ropes in the Heliosphere. Space Sci. Rev. 217, 38. doi:10.1007/s11214-021-00814-x
56. Khaborova, O., Zank, G., Li, G., Le Roux, J. A., Webb, G. M., Dosch, A., et al. (2015). Small-scale Magnetic Islands in the Solar Wind and Their Role in Particle Acceleration. I. Dynamics of Magnetic Islands Near the Heliospheric Current Sheet. Astrophys. J. 808, 181. doi:10.1088/0004-637X/808/2/181
57. Khaborova, O., Zank, G., Li, G., MalandrakiLe Roux, O. E. J. A., and Webb, G. M. (2016). Small-scale Magnetic Islands in the Solar Wind and Their Role in Particle Acceleration. II. Particle Energization inside Magnetically Confined Cavities. Astrophys. J. 827, 122. doi:10.3847/0004-637X/827/2/122
58. Klein, L. W., and Burlaga, L. F. (1982). Interplanetary Magnetic Clouds at 1 AU. J. Geophys. Res. 87, 613. doi:10.1029/ja087ia02p00613
59. Knetter, T., Neubauer, F. M., Horbury, T., and Balogh, A. (2003). Discontinuity Observations with Cluster. Adv. Space Res. 32 (4), 543–548. doi:10.1016/s0273-1177(03)00335-1
60. Knetter, T., Neubauer, F. M., Horbury, T., and Balogh, A. (2004). Four-point Discontinuity Observations Using Cluster Magnetic Field Data: A Statistical Survey. J. Geophys. Res. 109, A06102. doi:10.1029/2003ja010099
61. Lacombe, C., Salem, C., Mangeney, A., Hubert, D., Perche, C., Bougeret, J.-L., et al. (2002). Evidence for the Interplanetary Electric Potential? WIND Observations of Electrostatic Fluctuations. Ann. Geophys. 20, 609–618. doi:10.5194/angeo-20-609-2002
62. Lemaire, J., and Scherer, M. (1971). Simple Model for an Ion-Exosphere in an Open Magnetic Field. Phys. Fluids 14, 1683. doi:10.1063/1.1693664
63. Lemaire, J. (2010). Half a century of Kinetic Solar Wind Models. AIP Conf. Proc. 1216, 8. doi:10.1063/1.3395971
64. Lemons, D. S., and Feldman, W. C. (1983). Collisional Modification to the Exospheric Theory of Solar Wind Halo Electron Pitch Angle Distributions. J. Geophys. Res. 88, 6881. doi:10.1029/ja088ia09p06881
65. Lepping, R. P., Acũna, M. H., Burlaga, L. F., Farrell, W. M., Slavin, J. A., Schatten, K. H., et al. (1995). The WIND Magnetic Field Investigation. Space Sci. Rev. 71, 207–229. doi:10.1007/bf00751330
66. Lepping, R. P., Wu, C.-C., and Berdichevsky, D. B. (2005). Automatic Identification of Magnetic Clouds and Cloud-like Regions at 1 AU: Occurrence Rate and Other Properties. Ann. Geophys. 23, 2687–2704. doi:10.5194/angeo-23-2687-2005
67. Li, G., and Qin, G. (2011). A Solar Wind Model with Current Sheets. ASP Conf. Ser. 444, 117.
68. Li, G. (2008). Identifying Current-sheet-like Structures in the Solar Wind. ApJ 672, L65–L68. doi:10.1086/525847
69. Lie-Svendsen, Ø., and Leer, E. (2000). The Electron Velocity Distribution in the High-Speed Solar Wind: Modeling the Effects of Protons. J. Geophys. Res. 105, 35–46. doi:10.1029/1999ja900438
70. Macneil, A. R., Owens, M. J., Wicks, R. T., Lockwood, M., Bentley, S. N., and Lang, M. (2020). The Evolution of Inverted Magnetic fields through the Inner Heliosphere. Mon. Not. R. Astron. Soc. 494, 3655. doi:10.1093/mnras/staa951
71. Maksimovic, M., Pierrard, V., and Lemaire, J. F. (1997). A Kinetic Model of the Solar Wind with Kappa Distribution Functions in the corona. Astron. Astrophys. 324, 725.
72. Maksimovic, M., Zouganelis, I., Chaufray, J.-Y., Issautier, K., Scime, E. E., Littleton, J. E., et al. (2005). Radial Evolution of the Electron Distribution Functions in the Fast Solar Wind between 0.3 and 1.5 AU. J. Geophys. Res. 110, A09104. doi:10.1029/2005ja011119
73. Malandraki, O., Khabarova, O., Bruno, R., Zank, G. P., Li, G., Jackson, B., et al. (2019). Current Sheets, Magnetic Islands, and Associated Particle Acceleration in the Solar Wind as Observed by Ulysses Near the Ecliptic Plane. ApJ 881, 116. doi:10.3847/1538-4357/ab289a
74. Malara, F., Primavera, L., and Veltri, P. (1996). Gompressive Fluctuations Generated by Time Evolution of Alfvénic Perturbations in the Solar Wind Current Sheet. J. Geophys. Res. 101, 21597–21617. doi:10.1029/96ja01637
75. Mariani, F., Bavassano, B., Villante, U., and Ness, N. F. (1973). Variations of the Occurrence Rate of Discontinuities in the Interplanetary Magnetic Field. J. Geophys. Res. 78, 8011–8022. doi:10.1029/ja078i034p08011
76. Marsch, E. (2006). Kinetic Physics of the Solar corona and Solar Wind. Living Rev. Solar Phys. 3, 1. doi:10.12942/lrsp-2006-1
77. Matthaeus, W. H., Montgomery, D. C., Wan, M., and Servidio, S. (2012). A Review of Relaxation and Structure in Some Turbulent Plasmas: Magnetohydrodynamic and Related Models. J. Turb. 37, 1.
78. McComas, D. J., Bame, S. J., Feldman, W. C., Gosling, J. T., and Phillips, J. L. (1992). Solar Wind Halo Electrons from 1-4 AU. Geophys. Res. Lett. 19, 1291–1294. doi:10.1029/92gl00631
79. McCracken, K. G., and Ness, N. F. (1966). The Collimation of Cosmic Rays by the Interplanetary Magnetic Field. J. Geophys. Res. 71, 3315–3318. doi:10.1029/jz071i013p03315
80. Meyer-Vernet, N., and Issautier, K. (1998). Electron Temperature in the Solar Wind: Generic Radial Variation from Kinetic Collisionless Models. J. Geophys. Res. 103, 29705–29717. doi:10.1029/98ja02853
81. Meyer-Vernet, N., Mangeney, A., Maksimovic, M., Pantellini, F., and Issaurtier, K. (2003). Some Basic Aspects of Solar Wind Acceleration. AIP Conf. Proc. 679, 263. doi:10.1063/1.1618591
82. Miao, B., Peng, B., and Li, G. (2011). Current Sheets from Ulysses Observation. Ann. Geophys. 29, 237–249. doi:10.5194/angeo-29-237-2011
83. Michel, F. C. (1967). Model of Solar Wind Structure. J. Geophys. Res. 72, 1917–1932. doi:10.1029/jz072i007p01917
84. Moncuquet, M., Meyer-Vernet, N., Issautier, K., Pulupa, M., Bonnell, J. W., Bale, S. D., et al. (2020). First In Situ Measurements of Electron Density and Temperature from Quasi-thermal Noise Spectroscopy with Parker Solar Probe/FIELDS. ApJS 246, 44. doi:10.3847/1538-4365/ab5a84
85. Neugebauer, M., and Giacalone, J. (2010). Progress in the Study of Interplanetary Discontinuities. AIP Conf. Proc. 1216, 194. doi:10.1063/1.3395834
86. Neugebauer, M., and Giacalone, J. (2015). Energetic Particles, Tangential Discontinuities, and Solar Flux Tubes. J. Geophys. Res. Space Phys. 120, 8281–8287. doi:10.1002/2015ja021632
87. Ogilvie, K. W., Chornay, D. J., Fritzenreiter, R. J., Hunsaker, F., Keller, J., Lobell, J., et al. (1995). SWE, a Comprehensive Plasma Instrument for the WIND Spacecraft. Space Sci. Rev. 71, 55–77. doi:10.1007/bf00751326
88. Owens, M. J., Wicks, R. T., and Horbury, T. S. (2011). Magnetic Discontinuities in the Near-Earth Solar Wind: Evidence of In-Transit Turbulence or Remnants of Coronal Structure?. Sol. Phys. 269, 411–420. doi:10.1007/s11207-010-9695-0
89. Pecora, F., Greco, A., Hu, Q., Servidio, S., Chasapis, A. G., and Matthaeus, W. H. (2019). Single-spacecraft Identification of Flux Tubes and Current Sheets in the Solar Wind. ApJ 881, L11. doi:10.3847/2041-8213/ab32d9
90. Perkins, F. W., Barnes, C. W., Johnson, D. W., Scott, S. D., Zarnstorff, M. C., Bell, M. G., et al. (1993). Nondimensional Transport Scaling in the Tokamak Fusion Test Reactor: Is Tokamak Transport Bohm or gyro-Bohm?. Phys. Fluids B: Plasma Phys. 5, 477–498. doi:10.1063/1.860534
91. Phan, T. D., Gosling, J. T., Davis, M. S., Skoug, R. M., Øieroset, M., Lin, R. P., et al. (2006). A Magnetic Reconnection X-Line Extending More Than 390 Earth Radii in the Solar Wind. Nature 439, 175–178. doi:10.1038/nature04393
92. Pilipp, W. G., Miggenrieder, H., Mühläuser, K.-H., Rosenbauer, H., and Schwenn, R. (1990). Large-scale Variations of thermal Electron Parameters in the Solar Wind between 0.3 and 1 AU. J. Geophys. Res. 95, 6305. doi:10.1029/ja095ia05p06305
93. Pritchett, P. L. (2005). The “Newton Challenge”: Kinetic Aspects of Forced Magnetic Reconnection. J. Geophys. Res. 110, A10213. doi:10.1029/2005ja011228
94. Riazantseva, M. O., Budaev, V., Rakhmanova, L., Zastenker, G., Yermolaev, Y., Lodkina, I., et al. (2017). Variety of Shapes of Solar Wind Ion Flux Spectra: Spektr-R Measurements. J. Plasma Phys. 83, 705830401. doi:10.1017/s0022377817000502
95. Roth, M., De Keyser, J., and Kuznetsova, M. M. (1996). Vlasov Theory of the Equilibrium Structure of Tangential Discontinuities in Space Plasmas. Space Sci. Rev. 76, 251–317. doi:10.1007/bf00197842
96. Salem, C., Lacombe, C., Mangeney, A., Kellogg, P. J., and Bougeret, J.-L. (2003). Weak Double Layers in the Solar Wind and Their Relation to the Interplanetary Electric Field. AIP Conf. Proc. 679, 513. doi:10.1063/1.1618647
97. Scudder, J. D. (2019). Steady Electron Runaway Model SERM: Astrophysical Alternative for the Maxwellian assumption. ApJ 885, 138. doi:10.3847/1538-4357/ab4882
98. Servidio, S., Gurgiolo, C., Carbone, V., and Goldstein, M. L. (2014). Relaxation Processes in Solar Wind Turbulence. ApJ 789, L44. doi:10.1088/2041-8205/789/2/l44
99. Sheeley, N. R., and Rouillard, A. P. (2010). Tracking Streamer Blobs into the Heliosphere. ApJ 715, 300–309. doi:10.1088/0004-637x/715/1/300
100. Siscoe, G. L., Davis, L., Coleman, P. J., Smith, E. J., and Jones, D. E. (1968). Power Spectra and Discontinuities of the Interplanetary Magnetic Field: Mariner 4. J. Geophys. Res. 73, 61–82. doi:10.1029/ja073i001p00061
101. Telloni, D., Perri, S., Carbone, V., and Bruno, R. (2016). Selective Decay and Dynamic Alignment in the MHD Turbulence: the Role of the Rugged Invariants. AIP Conf. Proc. 1720, 040015. doi:10.1063/1.4943826
102. Trenchi, L., Bruno, R., Telloni, D., D’amicis, R., Marcucci, M. F., Zurbuchen, T. H., et al. (2013a). Solar Energetic Particle Modulations Associated with Coherent Magnetic Structures. ApJ 770, 11. doi:10.1088/0004-637x/770/1/11
103. Trenchi, L., Bruno, R., D’Amicis, R., Marcucci, M. F., and Telloni, D. (2013b). Observations of IMF Coherent Structures and Their Relationship to SEP Dropout Events. Ann. Geophys. 31, 1333–1341. doi:10.5194/angeo-31-1333-2013
104. Tu, C. Y., Wang, X., He, J., Marsch, E., and Wang, L. (2016). Two Cases of Convecting Structure in the Slow Solar Wind Turbulence. AIP Conf. Proc. 1720, 040017. doi:10.1063/1.4943828
105. Vasquez, B. J., and Hollweg, J. V. (1999). Formation of Pressure-Balanced Structures and Fast Waves from Nonlinear Alfvén Waves. J. Geophys. Res. 104, 4681–4696. doi:10.1029/1998ja900090
106. Vasquez, B. J., Abramenko, V. I., Haggerty, D. K., and Smith, C. W. (2007). Numerous Small Magnetic Field Discontinuities of Bartels Rotation 2286 and the Potential Role of Alfvénic Turbulence. J. Geophys. Res. 112, A11102. doi:10.1029/2007ja012504
107. Viall, N. M., and Borovsky, J. E. (2020). Nine Outstanding Questions of Solar Wind Physics. J. Geophys. Res. 125, e2018JA026005. doi:10.1029/2018ja026005
108. Viall, N. M., and Vourlidas, A. (2015). Periodic Density Structures and the Origin of the Slow Solar Wind. ApJ 807, 176. doi:10.1088/0004-637x/807/2/176
109. Viall, N. M., Kepko, L., and Spence, H. E. (2009). Relative Occurrence Rates and Connection of Discrete Frequency Oscillations in the Solar Wind Density and Dayside Magnetosphere. J. Geophys. Res. 114, A01201. doi:10.1029/2008ja013334
110. Viall, N. M., Spence, H. E., Vourlidas, A., and Howard, R. (2010). Examining Periodic Solar-Wind Density Structures Observed in the SECCHI Heliospheric Imagers. Sol. Phys. 267, 175–202. doi:10.1007/s11207-010-9633-1
111. Wang, Y.-M., Sheeley, N. R., Howard, R. A., Rich, N. B., and Lamy, P. L. (1999). Streamer Disconnection Events Observed with the LASCO Coronagraph. Geophys. Res. Lett. 26, 1349–1352. doi:10.1029/1999gl900177
112. Whittlesey, P. L., Larson, D. E., Kasper, J. C., Halekas, J., Abatcha, M., Abiad, R., et al. (2020). The Solar Probe ANalyzers-Electrons on the Parker Solar Probe. ApJS 246, 74. doi:10.3847/1538-4365/ab7370
113. Xu, F., and Borovsky, J. E. (2015). A New Four-Plasma Categorization Scheme for the Solar Wind. J. Geophys. Res. Space Phys. 120, 70–100. doi:10.1002/2014ja020412

Konflikt interesów: autorzy oświadczają, że badania przeprowadzono przy braku jakichkolwiek relacji handlowych lub finansowych, które można by interpretować jako potencjalny konflikt interesów.

Copyright © 2021 Borovsky, Halekas i Whittlesey. Jest to artykuł w otwartym dostępie, rozpowszechniany zgodnie z warunkami licencji Creative Commons Actiftion (CC BY). Użycie, dystrybucja lub reprodukcja na innych forach jest dozwolone, pod warunkiem podania pierwotnych autorów i właścicieli praw autorskich oraz powołania się na pierwotną publikację w tym czasopiśmie, zgodnie z przyjętą praktyką akademicką. Nie jest dozwolone użycie, dystrybucja lub reprodukcja, nie będąca w zgodzie z niniejszymi Warunkami.

---

Przetłumaczył: Łukasz Buczyński