Oscylacje, fale stojące i fizyczne standardy pomiaru

Oscylacje (pulsacje) to jedne z podstawowych form ruchu. Każda oscylacja istnieje sama z siebie, nie połączona z czymkolwiek, a będąc bez obserwatora nie posiada ilościowych parametrów i pomiarów. Po prostu istnieje! Do ustalenia tych parametrów i pomiarów potrzebny jest obserwator. Nie może on jednak nic powiedzieć o źródle oscylacji, dopóki nie ma w zasięgu innych źródeł. To, co może zrobić obserwator, to policzyć ilość oscylacji. Jeśli ma w pobliżu inny oscylator, ma szansę zrobić porównanie. Jako wynik porównania może określić jakieś źródła za szybsze od innych, tzn. mające większą częstotliwość.

Aby usystematyzować wyniki obserwacji, wybrano najstabilniejsze źródło, np., 1000 kawałków jego pełnych oscylacji zostaje uznane za początkowy standard trwania, zwany jednostką trwania (czasu).

Standard okresu czasowego dowiódł bycia użytecznym instrumentem w systematyzacji, pozwalającym określić dowolne źródło oscylacji z jednej, intuicyjnie zrozumiałej pozycji. Pomiar: kawałki oscylacji w pojedynczym okresie. A zatem, obserwator dokonuje pierwszego pomiaru: n kawałków na 1000 kawałków, gdzie 1000 kawałków jest standardem okresu (czasu). Pomiar taki może mieć dowolną nazwę, np. Hertz (kawałków na sekundę).

Co zrozumiałe, każdy standard, w tym standard czasu, jest niczym więcej jak ugodą opartą na tych samych oscylacjach: jednostka czasu jest zdeterminowana przez liczbę oscylacji czegoś. Początkowym pomiarem jednostek czasu są kawałki! Ale dla wygody konkretna liczba oscylacji czegoś konkretnego, ustalone przez porozumienie, nazwana została jedną sekundą – 1 s.

Ustalenie standardu długości, którego współczesna definicja wymaga pojęcia fali, wprowadza bardziej złożony problem. Metrologia ustaliła standard 1 metra na 1650763,73 kawałków długości fal Kryptonu⁸⁶, które, po raz kolejny, wypełniają konkretny dystans w przestrzeni.

Długość podróżujących fal zależy od częstotliwości oscylacji i zdolności ośrodka falowego do przenoszenia fal z konkretną prędkością. Zgodnie z efektem Dopplera, w układzie poruszającym się względem ośrodka falowego, długość biegnących fal zależy od prędkości układu: $\lambda =\left(c\pm V\right)/\nu$, a więc jest nie do zaakceptowania, że odległość przyjęta za 1 metr zawiera stałą liczbę fal biegnących, pochodzących z emisji Kryptonu⁸⁶ (transfer między poziomami 5d₅ → 2p₁₀).

Założenie, że długość fali w układzie nie zależy od jego prędkości, jest poprawne tylko wewnątrz teorii Newtona i Einsteina, które negują istnienie ośrodka falowego dla światła.

Problem ustalenia długości w fali elektromagnetycznej w próżni jest trudny. Wciąż nie znamy bezpośredniej metody pomiaru takiej fali w locie. Nie wiemy również, czy jest to nawet możliwe w teorii, żeby bezpośrednio zmierzyć falę biegnącą.

Fala stojąca, uformowana przez biegnące fale pierwotną i zwrotną, to całkiem inna kwestia. Dowiedziono wcześniej, podwójna długość fali stojącej daje stanowi długość fali biegnącej, które utworzą ją tylko w jednym przypadku: gdy układ jest nieruchomy (V = 0, 2λ_st = λ₁ − λ₂). Gdy układ się porusza w ośrodku (V > 0), prawdziwa staje się inna relacja:

${\mathrm{\lambda ’}}_{''st''}=\frac{{\stackrel{\→}{\lambda }}_1\cdot {\stackrel{\←}{\lambda }}_2}{{\stackrel{\→}{\lambda }}_1+{\stackrel{\←}{\lambda }}_2}$

(2.04)

która nie wskazuje na równość fali biegnącej i dwukrotnej fali stojącej. A zatem, gdy mówimy o standardzie długości, powinniśmy mówić o liczbie fal stojących w przestrzeni ustalonej jako 1 metr. Liczba ta wynosi 3301527,46 fal stojących z emisji Kryptonu⁸⁶.

Ale powstaje problem: kiedy prędkość układu zmienia zachowanie fal, zaprezentowany tu standard długości staje się wieloznaczny, ponieważ

${\mathrm{\lambda ’}}_{\mathrm{st}}={\lambda }_{\mathrm{st}}\cdot \frac{1-{\beta }^2}{\sqrt{1-{\beta }^2\cdot {sin}^2\theta }}$

(2.05)

Innymi słowy, jeżeli weźmiemy irydowo platynowy standard i policzymy liczbę fal stojących mieszczących się w jego długości, kiedy prędkość w ośrodku falowym jest zerowa (V = 0), potem policzymy je ponownie po zwiększeniu prędkości układu (V > 0), okaże się, że liczba fal również wzrosła. Nie obserwuje się tego w praktyce. Przez ponad wiek podnoszenia jakości standardu długości, nie odnotowano, zwiększenia lub zmniejszenia liczby fal stojących zawartych w długości 1 metra. Dlaczego?

Powód, dla którego niemożliwe jest to wykrycie może być wyjaśniony przez zależność rozmiarów poruszających się ciał od ich prędkości w ośrodku falowym, zgodnie z regułą:

Rozmiar ciała	Długość fali stojącej
$\Delta \mathrm{x’}=\Delta x\cdot \left(1-{\beta }^2\right)$	${\mathrm{\lambda ’}}_{\mathrm{st}}\left(x\right)={\lambda }_{\mathrm{st}}\cdot \left(1-{\beta }^2\right)$
$\Delta \mathrm{y’}=\Delta x\cdot \sqrt{1-{\beta }^2}$	${\mathrm{\lambda ’}}_{\mathrm{st}}\left(y\right)={\lambda }_{\mathrm{st}}\cdot \sqrt{1-{\beta }^2}$
$\Delta \mathrm{z’}=\Delta x\cdot \sqrt{1-{\beta }^2}$	${\mathrm{\lambda ’}}_{\mathrm{st}}\left(z\right)={\lambda }_{\mathrm{st}}\cdot \sqrt{1-{\beta }^2}$
$\mathrm{l’}=l\cdot \frac{1-{\beta }^2}{\sqrt{1-{\beta }^2\cdot {sin}^2\alpha }}$	${\mathrm{\lambda ’}}_{\mathrm{st}}={\lambda }_{\mathrm{st}}\cdot \frac{1-{\beta }^2}{\sqrt{1-{\beta }^2\cdot {sin}^2\alpha }}$

Hipoteza ta stanie się jasna, jeśli domniemana kompresja wymiarów ciała w układzie ruchomym zostanie porównana do kompresji fali stojącej w tym samym układzie.

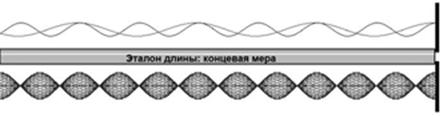
Taka synchronizacja możliwa jest tylko wtedy, gdy wiązania międzyatomowe w siatce krystalicznej mają naturę falową, i można je przedstawić w formie fal stojących.

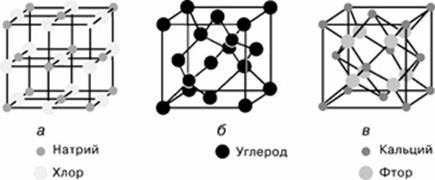
Il. 36. Struktura krystaliczna: a) halit NaCl; b) diament; c) fluoryt CaF₂. Złożone z różnych atomów, różnie ułożonych, wszystkie formują sześcian, czyli należą do tej samej grupy przestrzennej.

Jeśli wewnętrzna struktura materii będzie widziana w taki sposób, odległość między atomami będzie zawsze mierzona długością fali stojącej. Gdy prędkość ciała materialnego w ośrodku falowym się zwiększa, fala stojąca się kurczy (kompresuje), co prowadzi do redukcji dystansu pomiędzy atomami, a w rezultacie do zmniejszenia się rozmiarów poruszającego się ciała.

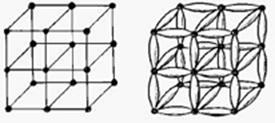
Il. 37. Wiązania w krysztale (z prawej) pokazane jako pakiet fal stojących, z atomami w węzłach.

Czy nie powinniśmy wyjaśnić, dlaczego wiązania międzyatomowe powinny być prezentowane jako fale stojące? Oraz dlaczego atomy powinny znajdować się dokładnie w węzłach oraz za nimi podążać, gdyby te z jakiegoś powodu się przesunęły?

Można to zrobić krok po kroku: 1) przeanalizować zachowanie modelu z pozycji falowej geometrii, oraz 2) uzasadnić przy pomocy znanych, klasycznych teorii, prawdopodobieństwo prezentowania wiązań materii jako fal, i 3) przeprowadzić eksperyment i porównać wyniki.

Przeanalizujmy pierwszy krok, w którym warunki ustalone są przy starcie przez geometrię falową.

Załóżmy dwa zgodne oscylatory, poszukujące takich miejsc względem siebie w przestrzeni falowej, że wzdłuż linii je łączącej emisja fal będzie całkowicie nieobecna. Taka minimalna możliwa pozycja wynosi długość fali stojącej (il. 38). Załóżmy warunek stabilności: oscylatory siedzą w węzłach fali stojącej przez nie wytworzonej, wzdłuż linii łączącej oscylatory zewnętrzna emisja jest nieobecna, liczba fal stojących (anty węzłów) pomiędzy oscylatorami jest liczbą całkowitą nieparzystą. Dodatkową zmienną jest przesunięcie fazy między oscylatorami.

Il. 38. Wzdłuż linii łączącej oscylatory brak jest zewnętrznej emisji (V = 0, Δφ = 0).

W takim układzie, z niezmienionymi parametrami, poruszającym się w ośrodku ze stałą prędkością, wzór interferencyjny się zmieni, tzn. warunek wewnętrznej równowagi zostanie złamany (il. 39). Możemy przywrócić równowagę poprzez zmianę parametrów.

Il. 39. Pojawia się zewnętrzna emisja (V > 0, Δφ = 0).

Aby w pełni przywrócić wewnętrzną równowagę w ruchomym układzie, należy po pierwsze zmienić odległość pomiędzy oscylatorami, zgodnie z 2.06, następnie utworzyć niezbędne przesunięcie fazy (2.07).

${\mathrm{\lambda ’}}_{\mathrm{st}}={\lambda }_{\mathrm{st}}\cdot \left(1-\frac{V^2}{c^2}\right)$

(2.06)

$\Delta \phi =\pi \cdot V/c$

(2.07)

Il. 40. Dzięki dokonanym zmianom (V > 0, Δφ = πV/c) wewnętrzna równowaga układu została przywrócona.

ale

$V/c=\Delta \phi /\pi$

(2.08)

co oznacza

${\mathrm{\lambda ’}}_{\mathrm{st}}={\lambda }_{\mathrm{st}}\cdot \left(1-\frac{{\Delta \phi }_2}{{\pi }_2}\right)$

(2.09)

Oznacza to, że w poruszającym się swobodnie układzie jego parametry: prędkość, długość i przesunięcie fazy są ze sobą ściśle powiązane, i muszą być razem koordynowane, aby zachować wewnętrzną równowagę.

A zatem, odkryliśmy, że ruch układu oscylatorów w ośrodku falowym prowadzi nie tylko do zwykłego zmniejszenia odległości miedzy oscylatorami, lecz wymaga również korekcji fazy pomiędzy źródłami falowymi. Prędkość układu i fazy oscylatorów mają dodatnią korelację. Jeśli następuje w linii oscylatorów, wówczas odległość pomiędzy nimi zmienia się wg wzoru:

${\mathrm{\lambda ’}}_{\mathrm{st}}={\lambda }_{\mathrm{st}}\cdot \left(1-\frac{V^2}{c^2}\right)$

(2.10)

Jeśli układ oscylatorów jest ustawiony poprzecznie do kierunku ruchu, wówczas, oprócz braku przesunięcia fazy ze względu na jego bezużyteczność w tym przypadku, odległość między oscylatorami zmniejszy się zgodnie ze wzorem:

${\mathrm{\lambda ’}}_{\mathrm{st}}=\frac{c}{2\nu }\cdot \sqrt{1-{\beta }_2}$

(2.11)

Wniosek: modelując ciało materialne jako pakiet fal, w których węzłach umieszczone są źródła falowe (atomy w ciele materialnym), wskazaliśmy na geometryczną przyczynę, która prowadzi do podłużnego i poprzecznego zmniejszenia pomiarów rozmiaru ciała w ruchu, tj. odkryliśmy algorytm zmian rozmiarów w zależności od prędkości w ośrodku falowym. Pojawia się kolejna ważna zależność: pomiędzy prędkością układu (w przypadku tylko dwóch oscylatorów), a przesunięciem fazy miedzy źródłami falowymi w układzie.

Przejdźmy do kolejnego kroku, bardziej związanego z rzeczywistą dynamiką. Przeanalizujemy tendencję oscylatorów do pozostawania w węzłach fal stojących, w przypadkach, gdy jakiś czynnik zewnętrzny próbuje je stamtąd przesunąć.

Zgodnie z klasyczną elektrodynamiką, atomy i molekuły oddziałują ze sobą głównie za pomocą sił elektromagnetycznych. W ciele stałym odległości pomiędzy atomami wahają się od 1 do 9 angstromów. Przypuśćmy, że wiązania międzyatomowe są natury falowo elektromagnetycznej, a minimalny możliwy dystans między atomami determinuje fala stojąca. Policzmy częstotliwość wiążącą się z oddziaływaniem.

$\nu =\frac{\mathrm{299\; 792\; 458}}{{10}^{-10}}=\mathrm{2,998}\cdot {10}^{18}\text{Hz}$

Jest to czynnik większy o dziesięć do czwartej potęgi od granicy światła widzialnego (częstotliwość światła niebieskiego – 6,3⋅10¹⁴Hz) i odpowiada zakresowi rentgenowskiemu. Mogłoby to wskazywać, że ciała stałe są zlokalizowanymi klastrami i źródłami emisji rentgenowskich. W takim wypadku powstaje pytanie: dlaczego te emisje są praktycznie nieobserwowalne?

Ów brak obserwacji można wyjaśnić następująco: wszystkie znane sposoby pomiaru oparte są na zasadzie porównania otrzymanej informacji z konkretnym standardem tła, zaakceptowanym jako zero. A zatem, jeśli czarne tło jest uznane za zero, każde odstępstwo od czerni można zaobserwować. Jeśli badany obiekt oraz otaczające go tło mają taką samą temperaturę, nie jest możliwym zmierzenie temperatury jednego obiektu przy pomocy drugiego. Odpowiednie narzędzia i organy, będące samemu źródłami promieniowania rentgenowskiego, nie potrafią wykryć ani tła przestrzeni, ani ciał o podobnej częstotliwości amplitudy, takich samych, jak w tle, ale przyjętych za zero. W rzeczywistości, poziom tła może być całkiem wysoki, ale dla nas i naszych urządzeń poziom ten odpowiada początkowemu punktowi odniesienia. Dlatego możemy zaobserwować tylko te obiekty, których emisje amplitudy i częstotliwości są wyższe od tła. Jest to promieniowanie o nadmiarowej amplitudzie, rejestrowane przez urządzenia.

A zatem wykrycie fal stojących będących w tle, czyli przyjętych za zero amplitudowe i częstotliwościowe, jest praktycznie niemożliwe. Intuicyjnie rozumiemy, że atomy potrafią tworzyć główne struktury z takich samych fal stojących, ale ich amplitudy i częstotliwości nie są białą plamą dla urządzeń. Wszystko, co się dzieje w tle, ma miejsce, ale nie może być bezpośrednio zaobserwowane. Istnieją jednak sytuacje, w których dwa podobne w składzie chemicznym i strukturze obiekty mogą wzajemnie rejestrować zwiększenie lub zmniejszenie swojej emisji rentgenowskiej. Jest to możliwe w polu grawitacyjnym, którego potencjał prowadzi do zsynchronizowanego obniżenia lub podwyższenia przesunięcia we wszystkich parametrach częstotliwości wewnątrz ciała. Ale na planecie Ziemi przesunięcia te są niezmiernie małe, porównywalne z grawitacyjnym przesunięciem ku czerwieni dowolnego źródła emisji.

Współczesne spojrzenie na naturę wiązań międzyatomowych jest dość niejasne i istnieje raczej na poziomie pojęć, niż modeli. Sam atom nie jest niczym więcej, jak wygodnym kluczowym pojęciem z szeregiem wyznaczonych eksperymentalnie własności. Wraz z odkryciami nowych własności, model się zmieniał (il. 41). Nie ma definitywnej odpowiedzi, jak dokładnie atomy się łączą w sieci krystalicznej, przy pomocy jakiego procesu?

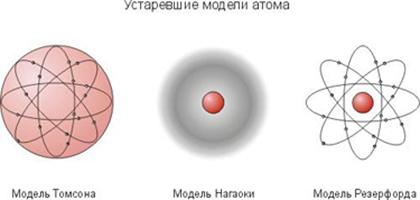
Il. 41. Thomson traktował atom jako elektrycznie neutralny kulisty układ, o średnicy około 10^-10m. Dodatni ładunek atomu jest równomiernie rozłożony wewnątrz atomu. Z prawe: model atomu Rutherforda i Nagaoki.

Załóżmy, że mamy dwa zgodne pulsujące źródła, wzbudzające ośrodek falowy, tworząc między sobą falę stojącą. Oscylatory ustawione są w węzłach fali, co daje prosty, minimalny, stabilny układ. Próby przesunięcia oscylatorów poza węzły wyzwalają reakcję pola falowego, skierowaną na przywrócenie oscylatorów do ich początkowych pozycji. Jeśli akcja dotyczy pojedynczego oscylatora, cały układ się przegrupowuje i zaczyna poruszać. Zagadnieniu temu zostanie poświęcony cały rozdział tej książki.

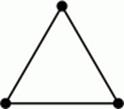
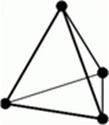
Il. 42 Dipol, trójkąt i czworościan są najstabilniejszymi układami, ponieważ pomiędzy źródłami, które je tworzą, znajduje się całkowita ilość połączeń, będących falami stojącymi.

Istnieją tylko trzy rodzaje idealnie stabilnych układów falowych o minimalnych wymiarach: dwa oscylatory i fala stojąca pomiędzy nimi, trzy oscylatory tworzący trójkąt równoboczny, z ramionami długości fali stojącej; cztery oscylatory tworzące czworościan foremny, o krawędzi długości fali stojącej (il. 43).

Wszystkie inne figury geometryczne połączone falami stojącymi posiadają interesujące, ułamkowe wiązania, w formie takich samych fal stojących. Zmniejszają one stabilność układu (il. 44).

Il. 45. Wzór rozkładu energii: a) dipol b) trójkąt c) kwadrat. Il. 45c pokazuje, że oscylatory znajdują się w regionach niezrównoważonych.

Wróćmy do kwestii standardu długości. Jeżeli podczas ruchu ma miejsce kompresja fali stojącej, wówczas, porównując konkretną liczbę fal stojących ze standardem długości, nie zauważymy żadnej kompresji. Fale stojące oraz wzorzec zachowują się podobnie, jak gdyby nic się nie stało, a kompresja nie miała miejsca. Taka sytuacja skłania do myślenia, że elektromagnetyczna natura wiązań międzyatomowych w standardzie oraz porównywanych ciałach jest podobna do fali stojącej. Wyjaśnia to niemożność wykrycia [kompresji], ponieważ obydwie fale stojące ulegają takiej samej kompresji.

Należy mieć na uwadze, że zarówno kompresja elektromagnetycznej fali stojącej, jak i skracanie wymiarów ciał materialnych, sa tylko hipotezami opartymi na poznanym zjawisku kompresji fal akustycznych. Użycie zjawiska w falach akustycznych jako bezpośredniej analogii fal elektromagnetycznych możliwe jest dzięki podobieństwu natury procesów oscylacyjnych, niemniej jednak robimy to tylko wewnątrz rozwijanego tu modelu. Tym bardziej, że Rytmodynamika jest oparta na oscylatorach, ośrodku falowym i falach.

Yuri N. Iwanow

Rytmodynamika – 2.03

Link do oryginału: http://www.rhythmodynamics.com/rd_2007en.htm#2.03