Eksperyment Michelsona jest dobrą ilustracją skrócenia wymiarów oraz wpływu tego zjawiska na skasowanie spodziewanych rezultatów. Przeanalizujmy to szczegółowo.
Jak przypuszczamy, rozmiary interferometru zmieniają się podczas ruchu przez ośrodek zgodnie z następującą regułą:
- (2.12)
θ jest kątem ustawienia interferometru względem kierunku ruchu.
- (2.13)
- (2.14)
W tych kierunkach fale stojące zmniejszają swoje rozmiary w tych samych proporcjach:
- (2.15)
- (2.16)
gdzie n
jest liczbą fal stojących, mieszczących się w ramionach interferometru.
Il. 46 Ogólny wygląd pierwszego interferometru Michelsona.
Jeśli teraz powtórzymy obliczenia Michelsona, biorąc pod uwagę skrócenie wymiarów, nie znajdziemy żadnej różnicy w czasie przejścia promieni.
Skrócenie wymiarów jest nieobecne, tzn. nie zależy od prędkości układu V:
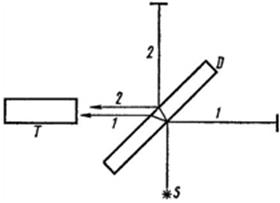
Il. 47. Ogólny schemat interferometru.
Przeanalizujmy eksperyment.
Załóżmy, że interferometr został ustawiony w taki sposób, że promień 1 porusza się z ruchem Ziemi, podczas gdy 2 jest do niego prostopadły. W takim przypadku, o ile eter nie jest wleczony przez ruch Ziemi, czas podróży promienia 1 wynosi:
- (2.17)
podczas gdy czas przelotu promienia 2 wynosi:
- (2.18)
A zatem, promienie 1 i 2 spędzą różny czas na pokonaniu drogi 2L, a różnica w czasie wynosi:
- (2.19)
Jeśli obrócimy urządzenie 90°, wówczas vice versa, czas zużyty przez promień 1 wyniesie:
- (2.20)
podczas gdy czas spędzony przez promień 2 wynosi:
- (2.21)
Ich różnica:
- (2.22)
Na skutek interferencji powinny się przesunąć prążki, i choć wielkość wielkości przesunięcia wynosi V2/c2, to jednak jest mierzalna. W konsekwencji, mając przesunięcie prążków, można ustalić prędkość wiatru eteru względem Ziemi.
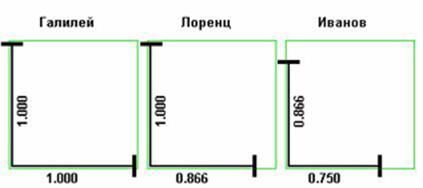
Il. 48. Długość ramion interferometru zależy od wyboru rodzaju skrócenia wymiarów. Obliczenia dotyczą V = 0,5c.
W Rytmodynamice skrócenie wymiarów podlega regule:
- (2.23)
- (2.24)
- (2.25)
Czas przelotu promienia 1 wyniesie:
- ,
- (2.26)
podczas gdy czas przelotu promienia 2 wynosi:
- (2.27)
A zatem czasy przejścia obu promieni, 1 i 2, są identyczne, a zatem
- (2.28)
Innymi słowy, czas przejścia (tam i z powrotem) promieni 1 i 2 nie zależy ani od orientacji interferometru względem ruchu, ani od prędkości w ośrodku falowym, tzn, zawsze jest stały. Łatwo jest wykazać na schemacie używanym przez zwolenników innego podejścia, mającym wyjaśniać spowalnianie czasu.
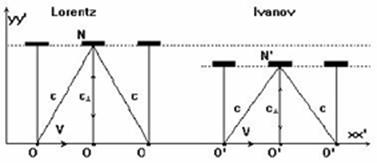
Il. 49. Schemat obliczania spowolnienia czasu.
Skrócenie wymiarów wg Lorentza pokazuje, że długość prostopadła nie zależy od prędkości V (L'(y,z)=L), a zatem obliczone kawałki czasu prowadzą do spowolnienia zegarów, zgodnie z regułą , czyli sekunda w poruszającym się układzie trwa dłużej. W rytmodynamice rozmiary poprzeczne zmieniają się zgodnie z regułą , co usuwa problem zależności jednostek czasu od prędkości: Δt’ = Δt.
Jeśli praca identycznych zegarów nie zależy od ich prędkości w ośrodku falowym, taka charakterystyka może posłużyć do zmierzenia prędkości światła w jednym kierunku. Ale najpierw opiszmy rytmodynamiczną interpretację eksperymentu Michelsona.
Yuri N. Iwanow
Rytmodynamika – 2.04
Link do oryginału: http://www.rhythmodynamics.com/rd_2007en.htm#2.04