W geometrii, nośnik konstrukcji pełni rolę absolutnego układu odniesienia (AUO). Jest to konieczne, w celu użycia geometrii euklidesowej w modelowaniu falowych procesów fizycznych. Bez nośnika, modelowanie procesów falowych jest niemożliwe, lub też jest możliwe po dodaniu dodatkowych otwartych warunków.
Istnieje szereg rodzajów geometrii:
- Geometria statyczna z ustalonymi punktami, figurami i relacjami pomiędzy nimi. W geometrii statycznej nie ma pojęcia czasu.
- Geometria kinematyczna, w której każdy punkt, linia czy figura porusza się, a relacje pomiędzy nimi ulegają zmianie, zgodnie z zestawem reguł. Geometria kinematyczna jest niemożliwa bez pojęcia czasu.
- Geometria falowa – odgałęzienie geometrii kinematycznej, nakierowana na studiowanie okresowych zjawisk falowych, procesów i relacji pomiędzy nimi. Geometria falowa oparta jest na aksjomacie nośnika konstrukcji, czyli
ośrodka falowego
. Wszystkie ruchy lub przemieszczenia w geometrii falowej zachodzą w nośniku konstrukcji, a zatem parametry tych ruchów i przemieszczeń zależą są mierzone w relacji z nośnikiem. Nośnik konstrukcji jest stałą, nie zmienia swojej formy bez względu na okoliczności. Służy tylko do pokazywania fal na sobie, tak samo, jak ruchu punktów, bezpośrednich linii oraz figur.
W naturze rolę nośnika konstrukcji pełni ośrodek falowy, przenoszący przez siebie samego zaburzenia, zawsze ze stałą prędkością (mowa o ośrodku liniowym, w którym co prawda nie może dojść do wymiany energii, ale jest łatwiejszy obliczeniowo – przyp. tłum.) oraz w relacji z samym sobą. Mając to wprowadzenie, przybliżyliśmy sobie geometrię falową do realnego, fizycznego ośrodka oraz fal. Różnica jest taka, że w geometrii falowej nośnik się nie odkształca, podczas gdy w rzeczywistości, np. na powierzchni wody czy w akustyce, fale bez deformacji ośrodka są niemożliwe. Tak jak w elektromagnetyzmie, nie mamy pojęcia, co się dzieje z ośrodkiem, gdy przebiega przez niego fala elektromagnetyczna.
Rhytmus: Po raz kolejny jest tu implikowany powrót eteru. Czy Michelson nie dowiódł, że on nie istnieje, ani istnieć nie może? Czy twoja specjalna opinia jest tylko odbiciem nostalgii?
Dynamicus: Ta opinia jest logicznie uzasadniona! Jedynym sposobem, aby dowieść braku ośrodka falowego, zwanego eterem
, jest zmierzyć prędkość światła w jednym kierunku. Tak długo, jak nie ma takiego eksperymentu, nie ma dowodu na brak eteru! Potrzebę tego eksperymentu podkreślano od czasów Jamesa Clarka Maxwella. Ale współczesny klan naukowy, rządzony przez interesy biznesu, jest niesłychanie nieentuzjastyczny wobec tej idei. Z tego powodu przypuszczalnie zarówno unikają wszelkich publicznych eksperymentów w tej dziedzinie, lub też jakieś wykonali, i trzymają je w sekrecie. Jeśli tak, każdy może powiedzieć, co oni robią za naukę
.
Weźmy przykład:
Załóżmy istnienie kropki (oscylatora) na dwuwymiarowym nośniku konstrukcji, emitującej okresowo fale w formie kołowych frontów. Każdy punkt fali jednorodnie oddala się od punktu emisji, z prędkością nadaną przez nośnik, nie przez źródło, które może się poruszać. Wokół źródła powstaje układ oddalających się frontów falowych. Jeżeli częstotliwość emisji jest stała, a źródło jest stacjonarne, odległości pomiędzy frontami są takie same, równe długości fali. Równomierny i liniowy ruch źródła (V < c) przesuwa pozycje frontów falowych w relacji z każdym. Same fronty pozostają kołowe, z centrum w miejscu ich emisji. Po emisji, front falowy nie zależy już dłużej od źródła ani innych frontów (Il. 4).
Klasyczne zasady dodawania prędkości można przedstawić jako:
- (1.02)
Zasada Dopplera:
- (1.03)
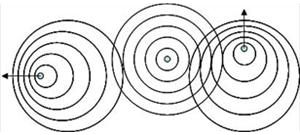
Brak nośnika prowadzi do dwuznaczności, zwłaszcza w sytuacji, gdy układ odniesienia ma być niezmiennikiem.
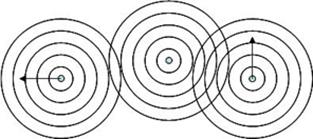
Jest to ciekawe, że geometria Euklidesa jest niekompatybilna z niezmienniczą teorią Galileusza. Niemożliwym jest skonstruowanie satysfakcjonującego wzoru interferencyjnego bez nośnika konstrukcji (…). Załóżmy na przykład, że dwa źródła o tej samej częstotliwości są niezmiennikiem. Prędkość jednego z nich będzie zero, a drugiego V. Skonstruujmy teraz zmienną w czasie interferencję fal ze źródeł (Il. 5.). To oczywiście nie jest możliwe bez złamania zasady niezmienniczości, gdyż fale mają być kołowe ze względu na równość źródła względem innych źródeł. W tym sensie geometria Euklidesa oraz niezmienniczosć przeczą sobie nawzajem: nie można prawidłowo skonstruować nawet najprostszej rzeczy, ponieważ współczesna fizyka i geometria euklidesowa są niekompatybilne.
Geometria falowa jest podstawą rytmodynamiki. Jej główne postulaty pokrywają się z podstawami geometrii falowej.
| Aksjomaty geometrii falowej | Postulaty rytmodynamiki |
|---|---|
|
|
Narzędzia geometrii falowej pozwalają modelować procesy oraz obliczać rezultaty eksperymentów. Tak przewidują (później zostanie to wykazane eksperymentalnie) kompresję fal stojących, w zależności od prędkości układu oscylatorów, która zależy od różnicy fazy; zależność przyspieszenia układu od różnicy częstotliwości, prędkość przepływu energii, istnienie energii o zerowej amplitudzie, etc.
Yuri M. Iwanow
Rytmodynamika – 1.04
Link do oryginału: http://www.rhythmodynamics.com/rd_2007en.htm#1.04