Fizyczne pochodzenie spinu elektronu
− używając struktury cząstki złożonej z fal kwantowych
Streszczenie
Pokazano, jak spin elektronu, oraz innych cząstek naładowanych, wyłania się ze struktury fal kwantowych materii. Spin jest rezultatem rotacji sferycznej w przestrzeni kwantowej fali dośrodkowej (pierwotnej) elektronu w jego centrum, gdy staje się ona falą odśrodkową (wtórną). Obrót fali wymagany jest do zachowania właściwych zależności fazowych w amplitudach fali. Rotacja sferyczna, będąca unikalną właściwością przestrzeni 3D, może być opisana grupą algebraiczną SU(2). W grupie tej, dośrodkowe oraz odśrodkowe fale cząstki naładowanej są elementami funkcji falowej spinoru Diraca. A zatem, wszystkie cząstki naładowane spełniają równanie Diraca.
Milo Wolff, Technotran Press
1124 Third Street, Manhattan Beach, CA 90266
milo.wolff@att.net
Wprowadzenie
P. A. M. Dirac oraz inni (Eisele, 1960) rozwinęli teorię matematyczną spinu elektronu, która odniosła duży sukces. Przewidziała ona odkrycie pozytronu (Anderson, 1922) oraz prawidłowo przewidziała wartość spinu, w jednostkach momentu kątowego. Aż do niniejszej publikacji, nie było zakończonej sukcesem próby fizycznego opisu spinu, ani żadnej sugestii jego pochodzenia, chociaż zdawano sobie sprawę, że jest to zjawisko kwantowe. Struktura elektronu, podobnie jak spin, była zagadką. Celem tej publikacji jest dostarczenie pierwszego fizycznego opisu pochodzenia spinu.
W pracy teoretycznej Diraca spin jest mierzony w jednostkach momentu kątowego, jak w przypadku obracającego się obiektu. Ale spin cząstki jest unikalnym fenomenem kwantowym, odmiennym od momentu kątowego w ludzkiej skali. Jego wartość jest ustalona i niezależna od masy cząstki czy jej prędkości kątowej. Aczkolwiek, własności spinu okazały się być powiązane z innymi własnościami kwantowej funkcji falowej elektronu. Chodzi o niezmienniczość parzystości (P), niezmienniczość czasu (T) oraz niezmienniczość ładunku (C). Na przykład, kantowa operacja CPT na cząstce jest niezmiennicza, CPT = {inwersja ładunku} × {inwersja parzystości} × {inwersja czasu} = niezmiennik.
Niniejsze studium powraca do propozycji, która była popularna sześćdziesiąt lat temu wśród pionierów teorii kwantowej: mianowicie, że materia składa się z falowych struktur przestrzeni. Proponuje się, że substancje materialne masy i ładunku w rzeczywistości nie istnieją, lecz są własnościami struktury falowej. Wyle, Schrödinger, Clifford i Einstein wierzyli, że cząstki mają strukturę falową. Wiara ta była spójna z teorią kwantową, gdyż matematyka kwantowa nie była zależna od istnienia substancji masy czy ładunku. W skrócie, zaproponowali oni, że fale kwantowe są realne, a masa i ładunek są tylko pozorami; mydlinami
wg słów Schrödingera. Realność fal kwantowych, zasugerowana przez Cramera (1986), wspiera oryginalną koncepcję Clifforda (1876), że cała materia jest po prostu falowaniem osnowy przestrzeni
.
Wheeler i Feynman (1945) jako pierwsi próbowali modelować elektron jako sferyczne fale elektromagnetyczne, dośrodkowe i odśrodkowe, poszukujące odpowiedzi Wszechświata (od pozostałej materii) aby wyjaśnić promieniowanie. Napotkali jednak trudności, gdyż nie było sferycznego rozwiązania dla fal elektromagnetycznych z użyciem pól wektorowych. Cramer (1986) zgłębiał odpowiedź rzeczywistych fal kwantowych. Używając równania fal kwantowych (pola skalarne), oraz fal sferycznych, Wolff (1990, ’91, ’93, ’95, ’97) odnalazł oraz opisał strukturę falową materii, która z sukcesem przewidywała Prawa Natury, mierzone eksperymentalnie. Przewidywała ona wszystkie właściwości elektronu, poza jedną – spinem. Teraz, niniejsza publikacja kompletuje owe przewidywania o fizyczne pochodzenie spinu, zgodne z teorią kwantową, równaniem Diraca, oraz poprzednio odkrytą strukturą elektronu.
Krótko podsumowując Wolffa, elektron składa się z dwóch zestawów fal sferycznych, dośrodkowego i odśrodkowego. Fale te nakładają się w swoim centrum, jak to pokazano na il. 1 w następnej sekcji, aby uformować pojedynczą rezonującą falę stojącą, której środek pokrywa się z lokalizacją elektronu. Odwrócenie fali dośrodkowej następuje w centrum, gdzie r = 0. Spin objawia się jako wymagany do tego procesu [trójwymiarowy] obrót, czyniący z fali dośrodkowej falę odśrodkową. Fale odśrodkowe, po napotkaniu innej materii we wszechświecie i zmodyfikowaniu jej fal, indukują odpowiedź Wszechświata. Niewielkie komponenty Huygensa powracają do źródła, i łączą się w falę dośrodkową. Ta prosta struktura, zwana rezonansem przestrzeni (SR), powoduje wszystkie eksperymentalne właściwości elektronu.
Struktura ta, własności elektronu, oraz prawa natury wynikają z trzech podstawowych zasad, lub założeń. Nie potrzeba żadnych innych praw, aby wyjaśnić prawa natury. W skrócie, brzmią one:
- Równanie falowe. Determinuje zachowanie fal kwantowych.
- Zasada gęstości fal. Ilościowe uogólnienie zasady Macha, które determinuje gęstość ośrodka fal kwantowych.
- Zasada minimalnej amplitudy (ZMA). Suma amplitud fal szuka minimum w każdym punkcie.
Następujące równanie falowe jest pierwszą zasadą.
2. Falowa struktura elektronu
Struktura elektronu zawiera rozwiązanie ogólnego równania falowego (Wolff, 1990). Równanie to opisuje zachowanie wszystkich fal cząstek w przestrzeni, i ma postać:
- (1)
gdzie Ψ jest skalarną amplitudą, c jest prędkością światła, a t jest czasem. Fale te są skalarnymi falami kantowymi, nie elektromagnetycznymi. równanie to posiada dwa sferyczne rozwiązania dla amplitudy elektronu: jednym z nich jest fala dośrodkowa, zmierzająca ku centrum, a drugą jest odśrodkowa fala rozbieżna. Rozwiązania mają postać:
- (2)
Gdzie
Fala dośrodkowa skupia się w centrum i obraca, aby stać się odśrodkową falą rozbieżną. Superpozycja ciągłych fal dośrodkowych i odśrodkowych formuje elektron, jak na il. 1, i nazywana jest rezonansem przestrzeni. Aby przekształcić falę dośrodkową w odśrodkową, otrzymując przy tym konstruktywną interferencję z właściwą relacją fazy, potrzebny jest obrót i przesunięcie fazy w centrum. Obrót ten daje spin o wartości , taki sam dla wszystkich naładowanych cząstek, gdyż wszystkie one współistnieją w tym samym wszechświatowym ośrodku falowym.
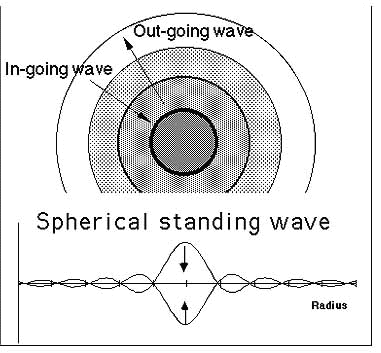
Il. 1. Struktura elektronu. Górny diagram pokazuje przekrój przez sferyczną strukturę, przypominającą warstwy cebuli. Składa się ona z poruszających się fal – dośrodkowej i odśrodkowej. Obie te fale łączą się, formując pojedynczą dynamiczną strukturę fali stojącej, w której centrum znajduje się umowne położenie elektronu. Zauważmy, że amplitudy fal kwantowych są wielkościami skalarnymi, a nie elektromagnetycznymi wektorami. Są one zatem częścią teorii kwantowej, nie elektromagnetycznej. Amplituda fal kwantowych w centrum jest skończona, podobnie jak potencjał elektryczny, co zgadza się z obserwacjami elektronu (Wolff, 1995). Niższy diagram pokazuje tą samą strukturę, rozrysowaną wzdłuż promienia od centrum elektronu. Jest on „plasterkiem” górnego diagramu.
3. Obrót sferyczny
Obrót fali dośrodkowej w centrum, w celu utworzenia fali odśrodkowej, jest absolutnie wymagany do zaistnienia struktury cząsteczkowej. Obrót w przestrzeni posiada warunki. Każdy mechanizm obracający (aby utworzyć kwantowy spin
) nie może zniszczyć ciągłości przestrzeni. Współrzędne krzywoliniowe przestrzeni w pobliżu cząstki muszą brać udział w ruchu cząstki. Na szczęście, natura posiada na to sposób – znany jako obrót sferyczny – unikalną właściwość przestrzeni 3D. W ujęciu matematycznym teorii grup w przestrzeni 3D, mechanizm ten jest opisany, tak, że wszystkie dozwolone ruchy muszą być reprezentowane przez grupę algebraiczną SU(2) wraz z potrzebną geometrią.
Obrót sferyczny jest niezwykłą właściwością przestrzeni 3D. Pozwala na obrót obiektu złożonego z przestrzeni wokół dowolnej osi, bez rozrywania współrzędnych przestrzeni. Po dwóch obrotach, przestrzeń odzyskuje pierwotną konfigurację. Właściwość ta pozwala elektronowi zachowywać zkwantowany spin
wokół wybranej osi, ponieważ fale dośrodkowe zbiegają do centrum, obracają się z przesunięciem fazy, aby stać się odśrodkowymi, po czym cykl się powtarza.
Wymagane przesunięcie fazy wynosi 180° obrotu, który zmienia amplitudę fali dośrodkowej w amplitudę fali odśrodkowej. Istnieją tylko dwa możliwe kierunki obrotu, zgodny ze wsk. zeg., oraz przeciwny (CW i CCW). Jeden odpowiada elektronowi ze spinem , drugi zaś jest pozytronem o spinie .
Niezwykłym jest pomyśleć, że gdyby przestrzeń 3D nie posiadała takiej geometrycznej właściwości jak obrót sferyczny, cząstki i materia, jakie znamy, nie mogłyby istnieć.

Il. 2. Wykres radialny przez strukturę elektronu Kiedy obie fale kwantowe się połączą, formują falę stojącą. Ten szczegółowy wykres, taki sam, jak przybliżony na il. 1, odpowiada dokładnie równaniu poniżej. Ogólny obrys amplitudy odpowiada potencjałowi Coulomba, z wyjątkiem centrum, gdzie ma on skończoną wartość, zgodnie z obserwacjami Lamba i Retherforda. Gdy elektron się porusza względem innego atomu obserwatora z prędkością v, na skutek efektu Dopplera na obu falach pojawia się długość de Broglie. Częstotliwość została po raz pierwszy zaproponowana przez Schrödingera i de Broglie’a, jest proporcjonalna do masy elektronu. Częstotliwość ta jest masą, więc pomiary masy są w zasadzie pomiarami częstotliwości. W przyrodzie nie ma substancji masy
.
4. Teoria spinu elektronu wg Diraca
Nowo odkryta mechanika kwantowa zaczęła być w latach 20-tych stosowana do fizyki cząstek, w poszukiwaniu zrozumienia tych drugich. Laureat nagrody Nobla, P. A. M. Dirac poszukiwał relacji pomiędzy teorią kwantową a zachowaniem energii w Szczególnej Teorii Względności, danej równaniem
- (3)
Dirac spekulował, że to równanie energii można przekształcić w równanie kwantowe w zwykły sposób, w którym energia E oraz moment pędu p zostałyby zastąpione przez operatory różniczkowe:
- oraz
- (4)
Miał nadzieję znaleźć kwantowe równanie różniczkowe cząstki. Na nieszczęście, (3) używało wielkości kwadratowych, a (4) nie. Droga była zamknięta. Dirac wpadł na dziwaczny pomysł. Spróbujmy znaleźć parametry (3) bez kwadratów, lecz pisząc równanie macierzowe:
- (5)
gdzie I jest macierzą jednostkową, a α i β są nowymi operatorami algebry wektorów.
Dirac był szczęśliwy. Odkrył, że jeżeli α będzie 4-wektorem, wówczas równanie (5) będzie działało bez zarzutu. Jest to słynne Równanie Diraca. Rónania (4) i (5) można połączyć, otrzymując .
W ogólności, Ψ jest czterowektorem: . Dla elektronu, redukuje się on do postaci .
Dirac zdał sobie sprawę, że dla elektronu potrzebne są tylko dwie funkcje falowe, Ψ3 i Ψ4. Przewidując one elektron oraz pozytron o energii E ze spinem:
oraz
Pozytron został odkryty pięć lat później przez Andersona (1931).
Dirac uprościł algebrę macierzy przez wprowadzenie 2-wektorów (par liczb), które nazwał spinorami
. Matryce spinów, operujące na wektorach, zdefiniowano następująco:
Dirac stworzył więc do opisu cząstek dwuliczbową algebrę, zamiast powszechnej jednoliczbowej. Ta spinorowa
algebra, choć wybitnie udana, była całkowicie teoretyczna i nie dawała adnych wskazówek co do fizycznej struktury elektronu. Teraz, w niniejszej publikacji, pokazane zostanie, że dośrodkowo-odśrodkowe fale kwantowe są fizyczną strukturą, odpowiadającą spinorowi Diraca. Dwie fale formują spinor, jak pokazano u Battey’a-Pratt’a (1986). Dwa fizyczne elementy spinorowe elektronu, lub też każdej naładowanej cząstki, są następujące:
- (6)
Przystepny opis Równania Diraca znajduje się u Eisele (1960).
5. Geometryczne wymagania dla spinu elektronu
Struktura cząstki zbudowanej z przestrzeni nastręcza problem, gdy rozważa się swobodne wirowanie cząstki. Jeśli część kontinuum jest częścią cząstki, to inna część przestrzeni przesuwałaby się po wirującej cząstce. W rezultacie linie współrzędnych mapujące całą przestrzeń zostały by skręcone i rozciągnięte bez żadnego ograniczenia. Struktura przestrzeni zostałaby rozdarta, jedna część przesuwałaby się obok drugiej wzdłuż rozdarcia.
Jeśli akceptujemy filozoficzną zasadę, że rozdzieranie przestrzeni
jest nie do zaakceptowania, musimy zapostulować, że grupy matematyczne ruchu cząstek są połączone i zwarte. W tym przypadku ruch w kontinuum będzie cykliczny a konfiguracja przestrzeni będzie cyklicznie się powracać do wcześniejszej, inicjacyjnej fazy. Czy to zachodzi w naturze? Tak, natura zawiera to wymaganie. Matematycy od dawna znają obrót sferyczny, właściwość przestrzeni 3D, w którym porcja przestrzeni może się obrócić i powrócić identyczna do poprzedniego stanu po dwóch obrotach. Ten niezwykły ruch opisany został w Scientific American (Rebbi, 1979) oraz w książce Gravitation (Misner et al., 1973). Jest to podstawa spinu, opisywanego w tym artykule.
Jakie są geometryczne wymogi dla ruchu cząstki, aby nie zniszczył on ciągłości przestrzeni? Współrzędne krzywoliniowe muszą uczestniczyć w ruchu cząstki. Wymóg ten jest zgodnie z teorią grup w przestrzeni 3D spełniony przy założeniu, że wszelki ruch opisany jest spójną, prosto połączoną grupą. Najprostszą taką grupą dla ruchu cząstki o sferycznej symetrii jest SU(2). Grupa ta daje wszystkie potrzebne i znane właściwości spinu cząstek naładowanych, takich jak elektron.
6. Zrozumienie obrotu sferycznego
Ów rzadko studiowany ruch można zamodelować przez piłkę, przymocowaną sznurkami do ramy. Sznurki reprezentują współrzędne przestrzeni, obracająca się piłka – właściwość przestrzeni w centrum naładowanej cząstki, złożonej ze schodzących się i rozchodzących fal kwantowych. Piłka może zostać obrócona wokół dowolnej osi z dowolnej pozycji początkowej. Jeśli obracać piłką w nieskończoność, okaże się, że po każdych dwóch obrotach znajdzie się ona w pierwotnej pozycji.
W tradycyjnej analizie obracających się obiektów, zwykle zakłada się, że odwrócenia osi wirowania jest równoważny z odwróceniem samego wirowania. Niemniej jednak, w przypadku elektronu, który jest w sposób ciągły połączony ze swoim otoczeniem, jako część otaczającej go przestrzeni, przestaje być to prawdą. Należy uczynić tu rozróżnienie pomiędzy inwersją a rewersją spinu cząstki. Rozróżnienie to prowadzi do jednej z najpodstawowszych właściwości cząstek.
Aby odwrócić oś spinu, można odwrócić czas (t → -t), lub prędkość kątową (ω → -ω). Obie operacje sprowadzają się do zamiany fali wchodzącej elektronu z wychodzącą. Spinory przyjmą wówczas postać:
Aby wynicować oś spinu struktury cząstki, niezbędne jest obrócenie struktury wokół którejś z osi prostopadłej do osi spinu, z, np. wokół y. Wówczas wynicowany spin dany jest operacją odwracania macierzy:
A zatem, inwersja i rewers to nie to samo. Różnica pomiędzy tymi operacjami jest charakterystyką kwantowej natury elektronu. Są one różne od ludzkiego spojrzenia na obracające się obiekty i są ważne do zrozumienia struktury cząstek.
7. Matematyka grup obrotu sferycznego
Każda konfiguracja sferycznie obracającej się piłki (lub centrum elektronu) może być reprezentowana przez punkt w euklidesowej 4D hipersferze, będącej jednocześnie przestrzenią grupy matematycznej SU(2). Obrót w trybie sferycznym można reprezentować każdym operatorem transformującym jeden wektor w inną pozycję. Zwykle przypisuje się sferze promień jednostkowy. Wówczas obrót piłki można opisać grupą SU(2). Wygodnie jest również umiejscowienie centrum jednostkowej hipersfery w początku [układu współrzędnych] i uczynienie wektora [1, 0, 0, 0] reprezentacją konfiguracji początkowej. Jakakolwiek inna konfiguracja wybierana jest często symbolami (a, b, c, d). Wówczas .
Powszechną reprezentacją wektorów hipersfery jest notacja kwaternionowa:
Można wykazać (Battey-Pratt & Racey, 1986), że operator kwaternionowy 4×4 jest odpowiednikiem operatora 2×2 jak poniżej:
gdzie elementy macierzy, będące często 0 lub 1, są liczbami zespolonymi. Można zobaczyć, że wyznacznik również wynosi , jak powyżej. Spinorowa (operacyjna) forma amplitudy wynosi:
Jest to notacja spinorowa, wymyślona przez Diraca do reprezentowania konfiguracji elektronu, jak pokazano w Tabeli 1. Reprezentuje ona również obroty w trybie sferycznym, będące elementami zamkniętej, uni-modularnej grupy SU(2).
| Operacja (symbol Diraca) |
Operator SU(2) | Początkowy spinor SU(2) | Końcowy spinor SU(2) | Odpowiadający operator kwaternionowy |
|---|---|---|---|---|
| Zostaw przestrzeń, jak jest. [I] |
1 | |||
| Obróć przestrzeń o 180° wokół osi x. Spin-x |
i | |||
| Obróć przestrzeń o 180° wokół osi y. Spin-y |
j | |||
| Obróć przestrzeń o 180° wokół osi z. Spin-z |
k |
Dla przykładu, sferyczne fale kwantowe w przestrzeni mogą zostać obrócone o 180° wokół osi z przez operator spin-z. Gdy mamy do czynienia z ciągłym obrotem fali kwantowej w przestrzeni z predkością kątową, spinor reprezentowany jest przez:
8. Jak spin wyłania się z falowej struktury elektronu
Falowa struktura elektronu składa się ze sferycznych fal dośrodkowych i odśrodkowych, poruszających się z prędkością światła c (Wolff, 1990, 1993, 1995). Ilustracje1 i 2 pokazują strukturę elektronu, zwaną rezonansem przestrzeni. Fale odśrodkowe elektronu podróżują do pozostałej materii we Wszechświecie i komunikują się z nią. Gdy fale te docierają do materii, ich sygnatura zmienia się w falę odśrodkową tejże materii. Fala ta jest odpowiedzią (Wheeler & Feynman, 1945; Cramer, 1986; Ryazanov, 1991) od pozostałej materii. Całkowita odpowiedź falowa, jako kombinacja Fouriera, staje się falą dośrodkową początkowego elektronu. Powracające fale zbieżne skupiają się w centrum pierwotnego elektronu, po czym odbijają się z przesunięciem fazy, które je obraca do postaci fal wyjściowych. Cykl się powtarza.
Centralne przesunięcie fazy podobne jest do przesunięcia fazy w świetle odbitym od lustra. Wymaganym kątem odbicia jest 180° Cw lub CCW. Są tylko dwie możliwe kombinacje obracających się na zewnątrz i do środka fal. Jeden rodzaj rotacji jest elektronem, a drugi pozytronem. zmiana momentu kątowego rotacji wynosi lub . Jest to przyczyna spinu. Jeden zestaw fal jest lustrzanym odbiciem drugiego, dając zasadę niezmienniczości CPT.
9. Wnioski
9.1 Kompletny zestaw właściwości elektronu
Pochodzenie spinu kompletuje właściwości elektronu. Wszystkie je można obecnie wyprowadzić ze struktury rezonansu przestrzeni, oraz pasują do wszystkich eksperymentalnych obserwacji elektronu. Panuje obecnie lekka wątpliwość, czy materia skomponowana jest ze sferycznych struktur fal kwantowych, podlegającym trzem zasadom falowej budowy materii. Zauważmy jednak, że spin, oraz inne właściwości, są raczej atrybutami przestrzeni kwantowej, niż indywidualnych cząstek. Jest to przyczyna, dla której spin, podobnie jak ładunek, ma tylko jedną wartość dla wszystkich cząstek. Wartość ta zależy od struktury przestrzeni.
9.2 Wszechświat fal kwantowych i przestrzeni
Chociaż spin fascynował fizyków przez 60 lat, nie był sam w sobie istotnym rezultatem. Zamiast tego, najbardziej niezwykłym wnioskiem z falowej struktury elektronu jest to, że prawa fizyki i natury wynikają z fal pochodzących od całej materii Wszechświata. Każda cząstka komunikuje swój stan falowy całej reszcie materii, tak więc struktura cząstki, wymiana energii oraz prawa fizyki są własnościami całego układu. Jest to przyczyna zasady Macha. Uniwersalne właściwości fal kwantowych przestrzeni odpowiadają również za uniwersalny zegar oraz stałe natury.
Struktura ta rozstrzyga trwający od wieku paradoks, czy cząstki są falami, czy też punktowymi bitami materii. Są one falowymi strukturami przestrzeni. Nie ma nic, poza przestrzenią. Jak spekulował Clifford 100 lat temu, materia jest po prostu falowaniem osnowy przestrzeni
.
9.3 Prosty elektron
Elegancją struktury elektronu jest jej podstawowa prostota. To tylko dwie sferyczne fale, falujące wdzięcznie wokół centrum, przemieniając się między sobą. Ta sferyczna struktura falowa łączy się z falami innych naładowanych cząstek, tworząc miriady struktur fali stojącej. Struktury te stają się krystaliczną materią w stanie stałym. Jeśli możesz dostrzec strukturę falową, kryształ jawi się jako wiele lśniących baniek, połączonych w geometryczny łańcuch. Łańcuchy te są trzymane razem przez niezwykłą sztywność – właściwość przestrzeni.
Następnym krokiem nauki w przyszłości będzie zrozumieć naturę struktury przestrzeni.
10. Bibliografia
- Apeiron, v2, nr 4, paźdź. 1995. Zawiera osiem artykułów traktujących o różnych interpretacjach teorii kwantowej.
- E. Battey-Pratt, and T. Racey (1980) „Geometric Model for Fundamental Particles,” Intl. J. Theor. Phys. 19, 437-475. Rozpoznali oni, że spin elektronu jest geometryczną właściwością przestrzeni i może istnieć w strukturze sferycznej.
- Louis Duc de Broglie (1924), PhD thesis „Recherché sur la Theorie des Quanta,” U. of Paris. Zaproponował on długość fali λ=hp fal kwantowych elektronu, zawierającego oscylator o częstotliwości mfrac>mc2h, jako rezonans przestrzeni.
- William Clifford (1956), „On the Space Theory of Matter” The World of Mathematics , s. 568, Simon & Schuster, NY. Angielski matematyk Królewskiego Stowarzyszenia Filozoficznego, jako pierwszy zasugerował (1876), że materia składa się wyłącznie z fal.
- John Cramer (1986), „The Transactional Interpretation of Quantum Mechanics”, Rev. Mod. Phys 58, 647-687. Interpretował fale mechaniki kwantowej jako rzeczywiste, w przeciwieństwie do popularnych
fal prawdopodobieństwa
. Wprowadził pojęcie fali oferującej (odśrodkowej) i fali odpowiedzi (dośrodkowej). - John A. Eisele (1960), Modern Quantum Mechanics with Applications to Elementary Particle Physics . Wiley- Interscience, (John Wiley & Sons, NY, London). Książka ta omawia w szczegółach równanie Diraca.
- C.W. Misner, K. Thorne, and J.A. Wheeler (1973), Gravitation , W.H. Freeman Co. p1149. Książka zawiera wiele pionierskich pomysłów, włącznie z obrotem sferycznym.
- C. Rebbi (1979) „Solitons” Scientific American, Feb., 92, 168. Omawia rotację sferyczną w odniesieniu do solitonów.
- Giorgi Ryazanov (1991), Proc. 1st Int’l Sakharov Conf. Phys., Moscow, May 21-31, pp. 331-375, Nova Sci. Publ., NY. Użył metody Wheelera-Feynmana do wydedukowania, że prawa natury są odpowiedzią Wszechświata.
- J. Wheeler and R. Feynman (1945), „Interaction with the Absorber as the Mechanism of Radiation,” Rev. Mod. Phys. 17, 157. Zamodelowali elektron jako dośrodkowe i odśrodkowe fale, aby prześledzić transfer energii do absorbera.
- Milo Wolff (1990), Exploring the Physics of the Unknown Universe , ISBN 0-9627787-0-2. (Technotran Press, CA). Przystępne zagłębienie się w prawa natury, z implikacjami dla cząstek oraz kosmologii.
- Milo Wolff (1991), „Microphysics, Fundamental Laws and Cosmology”. Proc. 1st Int’l Sakharov Conf. Phys., Moscow, Maj 21-31, s. 1131-1150, Nova Sci. Publ., NY.
- Milo Wolff (1993), „Fundamental Laws, Microphysics and Cosmology,” Physics Essays 6, s. 181-203.
- Milo Wolff (1995), „Beyond the Point Particle – A Wave Structure for the Electron,” Galilean Electrodynamics 6, nr 5, s. 83-91.
- Milo Wolff (1997A) „Exploring the Universe and the Origin of it Laws,” Temple University Frontier Perspectives 6, nr. 2, s. 44-56.
- Milo Wolff (1997B) „The Eight-Fold Way of the Universe,” Apeiron 4, nr. 4. Wrzesień (1997).
Link do oryginału: http://mwolff.tripod.com/body_spin.html