Efekt Kerra, w optyce geometrycznej, jest rozszerzeniem zasad załamania światła podczas jego przechodzenia przez przejrzysty materiał o zmiennym indeksie refrakcji. Efekt ten stał się ważny w przemyśle telekomunikacyjnym, dla włókien optycznych (włókna o zmiennym indeksie załamania).
Efekt Kerra używany jest do ominięcia rozpraszania kolorów podczas transmisji światła. W rezultacie na całej długości trasy zachowana zostaje relacja fazy w widmie transmitowanego światła, a tym samym przenoszona informacja (soliton).
Może się okazać, że w astrofizyce efekt ten ma niespodziewane zastosowanie w środowisku gazowym o gradiencie w poziomie refrakcji, wraz z powiązaniem z gradientem gęstości (masy). Szczególnie gdy środowiska te występują wraz z gigantycznymi czarnymi dziurami (centra galaktyk).
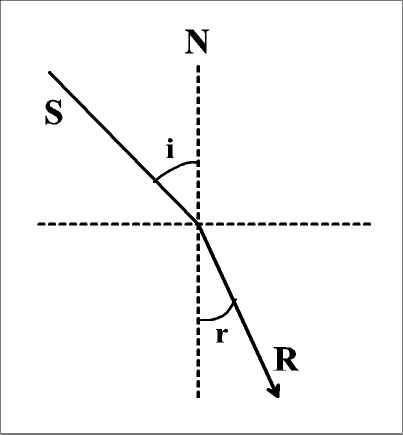
Optyczne prawa Kartezjusza (przypomnienie)
Padający promień, prostopadły do padania oraz promień ugięty są na tym samym planie.
Sinus kąta padania jest w stałej relacji do sinusa kąta ugięcia. Wyraża to zależność:
sin i = n ⋅ sin r (n jest indeksem refrakcji)
Zauważmy, że indeks ugięcia zależy również od częstotliwości padającej fali. To właśnie ta własność jest wykorzystywana we włóknach z gradientem padania w celu uniknięcia rozproszenia chromatycznego.
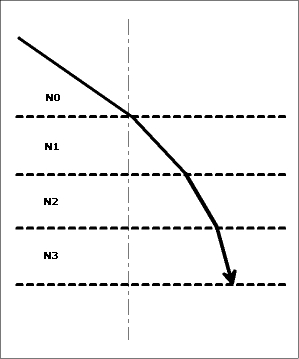
Efekt Kerra w płaskiej geometrii
Gdy światło przecina środowisko o ciągłej zmianie indeksu refrakcji, podąża ono po trajektorii o stale zmieniającym się kącie. Na przykład, po lewej widać światło szybko zmieniające kierunek na pionowy.
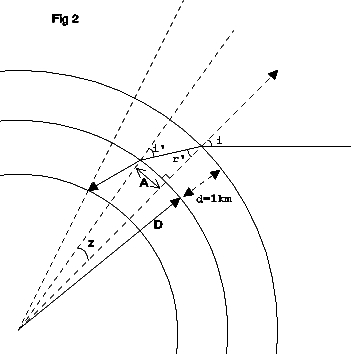
Efekt Kerra w geometrii kołowej lub sferycznej (fr, PDF)
W środowisku sferycznym, z indeksem refrakcji zwiększającym się z zewnątrz do wewnątrz, światło podąża torem spiralnym. rodzaj spirali zależy od szybkości zmiany indeksu (liniowa, kwadratowa, sześcienna…).
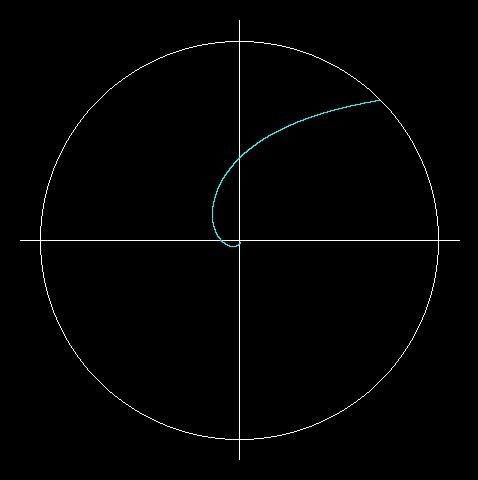
Algorytm symulacji:
Osiągnęliśmy tą symulację dzięki programowi napisanemu w języku C. Czas wykonania, po kompilacji, na naszym PC, posiadanym w owym czasie (486 DX 50), był rzędu pół godziny.
Użyliśmy, za radą J.C. Peckera, profesora na Collège de France, prawa doskonałego szkła, pozwalającego na policzyć indeks załamania, znając gęstość n (ilość molekuł na objętość).
Dla obliczeń czynnika załamania ułożyłem równanie:
gdzie α = 0,91 (wodór), a v = częstotliwość.
Potem wsadziliśmy to do oprogramowania zawierającego drugie prawo Kartezjusza. Trudności obliczeniowe wynikały z małej dokładności procesora (tabele trygonometryczne były wówczas ograniczone do 32 bitów, lepiej zatem było obliczać je samodzielnie). Poza tym nie należy zapominać o przybliżeniu obliczeń. finałem jest wynik dla sfery gazu wielkości około stu lat świetlnych, o gęstości zmieniającej się od 10-20 g/cm3 do 10-10 g/cm3.
Gęstość rosła kwadratowo. Pokazano tu tylko część centralną. Symulacja pokazuje również, że częstotliwość optyczna jest zaniedbywalna przy takich gęstościach materii.
Nie ukrywając, gdy wykonałem tą pracę, nikt mi nie wierzył, nawet ja sam sobie.
Wnioski
Jeżeli we Wszechświecie zjawiska ugięcia światła są takie, jak w bąblu gazowym z gradientem gęstości materii oraz refrakcji, wówczas, co ewidentne, jest zupełnie zbędnym, aby widząc soczewkę, za każdym razem odwoływać się do grawitacji. Jednakowoż te dwa zjawiska się nie wykluczają. A w tym przypadku dodają się i nakładają!
Autor: Bernard Lempel (![]() )
)
Przetłumaczono z: KERR EFFECT IN OPTICS
Przetłumaczył: Łukasz Buczyński