Streszczenie: oryginalny pomysł de Broglie, że elektron posiada wewnętrzny zegar, otrzymał niedawno potwierdzenie eksperymentalne poprzez pomiar okresu tego zegara w eksperymencie z tunelowaniem. Wynik ten został wyjaśniony nowym modelem elektronu, zwanym modelem drgającym, gdyż wykorzystuje on jakościową koncepcję Schrödingera ruchu drgającego (zitterbewegung) w w pełni określonym modelu reagującej cząstki. Drgający elektron jest podobną do światła cząstką naładowaną z wewnętrznym spinem, który utrzymuje ją na helikalnej ścieżce w czasoprzestrzeni, o krzywiźnie i częstotliwości określonej masą elektronu. Zatem masa elektronu jest w pełni zredukowana do częstotliwości zegara w ruchu elektronu. Niniejszy esej omawia szczegóły modelu i jego implikacje.
Aby odkryć naturalną skalę czasu, patrzymy na dynamikę cząstek elementarnych. Louis de Broglie był pierwszym, który to zrobił, gdy w swojej tezie doktoranckiej z 1924 roku zaproponował istnienie wewnętrznego zegara elektronu. Jako dwa filary mechaniki kwantowej, zaakceptował prawo Plancka:
- (energia jest częstotliwością!)
- (1)
oraz prawo Einsteina:
- (masa jest energią!)
- (2)
Stosując oba te prawa do elektronu (o masie spoczynkowej mc), zaproponował
- (masa jest częstotliwością!)
- (3)
dla częstotliwości zegara elektronu. Zegar można modelować funkcją okresową
- (4)
gdzie τ jest właściwym czasem wzdłuż trajektorii elektronu w czasoprzestrzeni.
De Broglie poszedł dalej i zaproponował, że z ruchem elektronu skojarzona jest fala o tej samej częstotliwości [1]. Jak wszyscy wiedzą, ta hipoteza falowa została natychmiast rozszerzona przez Schrödingera w jego słynne równanie falowe, które stało się paradygmatem mechaniki kwantowej. Co ironiczne, hipoteza zegarowa de Broglie została zignorowana lub zapomniana w fizycznej literaturze naukowej. Z resztą, jak zmierzyć czas zegarem o okresie 1021 sekund?
Minęło wiele dekad, zanim francuski fizyk doświadczalnik, Michel Gouanère, znalazł sposób poszukiwania zegara elektronu. Przypuszczam, że musiał on być francuskim doświadczalnikiem, aby potraktować hipotezę zegarową poważnie, gdyż spojrzenie de Broglie’a na mechanikę kwantową zostało odrzucone lub oczernione przez większość teoretyków, z wyjątkiem niewielkiej grupy (przeważnie francuskich) entuzjastów.
Z tego, co mi opowiadał, Gouanère omawiał wiele eksperymentalnych możliwości ze swoim kolegą M. Spighel’em, dopóki nie doszli do tunelowania elektronu jako wykonalnej możliwości. W eksperymencie z tunelowaniem, elektrony, będące w wiązce niemal równoległej do osi kryształu, są więzione na orbitach, spiralując wokół pojedynczych szeregów atomowych, zatem rozpraszanie jest redukowane i znacznie zwiększa się transmisja przez kryształ. Gouanère twierdził, że jeżeli elektron wewnętrzny zegar elektronu jest fizycznie rzeczywisty, tunelowane elektrony powinny oddziaływać w sposób rezonujący z okresowością kryształu na pewnej energii, produkując spadek tempa transmisji.
Przewidywana energia rezonansu jest łatwa do wyliczenia. Jak już zauważył de Broglie, częstotliwość zegara, zaobserwowana w laboratorium ωL w czasie laboratoryjnym t powiązana jest z częstotliwością zegara wewnętrznego wzorem , zatem
- , gdzie
- (4)
jest czynnikiem relatywistycznej dylatacji czasu, a v jest laboratoryjną prędkością elektronu, równoległą do osi kryształu. Zatem odległość mierzona w okresie zegara wynosi
.
Wzdłuż osi [1, 1, 0] kryształu silikonowego, odległość między atmoami d = 3.84 Å, zatem przewidywana energia rozonansowa wynosi:
- (5)
.
Mieści się to z łatwością w przedziale energii dostepnych w eksperymencie z tunelowaniem.
Wiedzieli oni, że zebranie funduszy na tak niecodzienny eksperyment będzie niemożliwe do zagwarantowania, dlatego zorganizowali oni zespół badawczy i i napisali projekt badań promieniowania Koumakhova
w przedziale 54 do 110 -MeV w liniowym akceleratorze w Saclay. Dopóki projekt nie wystartował, nie poinformowano innych członków zespołu, co tak na prawdę planowano zrobić. Na eksperyment zegarowy przeznaczono jeden dzień czasu akceleratora, jednak publikacja opóźniła się wiele lat, dopóki nie ukończono analizy danych!
Eksperyment obejmował poszukiwanie rezonansu transmisji w tunelowanym strumieniu elektronów, poprzez skanowanie okna energii, wyśrodkowanego na przewidywanym momencie rezonansu (5). Odnaleźli oni 8% spadek w transmisji, wyśrodkowany na . różnica 0,28% pomiędzy spodziewaną a zmierzoną wielkością mieściła się w otrzymanym błędzie kalibracji ±0,3%, chociaż Gouanère wyznał mi, że myślał, iż eksperyment był dokładniejszy.
Ich wyniki zostały opublikowane Annales de la Fondation Louis de Broglie w 2005. Jak się spodziewano, odzew był nikły, gdyż to czasopismo przyciąga niewielu czytelników. Aby się bardziej uwidocznić, Gouanère wysłał nieco zmodyfikowany raport do Physical Review Letters. Zostal on odrzucony w styczniu 2007. Wiekszość recenzentów twierdziło, że wyniki są fizycznie nieprawdopodobne! Ich reakcja przypomina mi ironiczną wypowiedź Eddingtona Nie uwierzę w eksperyment, dopóki nie zostanie potwierdzony przez teorię!
. Tym niemniej, jeden z recenzentów zasugerował, że efekt może być wyjaśniony przez ruch drgający (zitterbewegung) Schroedingera. Gouanère nigdy nie słyszał o zitterbewegung, zatem użył wyszukiwarki Google i znalazł mój artykuł [2], w którym argumentowałem, że zitterbewegung jest fundamentalny dla interpretacji równania Diraca i à fortiori dla interpretacji mechaniki kwantowej.
Spotkaliśmy się w Paryżu w maju 2007 roku. Gouanère opowiadział mi dokładniej o eksperymencie i przekonywał, że wyniki powinny być potraktowane bardziej serio. Zdarzyło się, że gdy pracowałem nad modelem drganiowym elektronu, czekając na możliwość wypracowania jego eksperymentalnych zastosowań. Jako, że eksperyment Gouanère’a oferował bezpośredni test dla modelu, skożystałem z okazji, aby wyjaśnić dane ilościowo. Wyniki nie mogły być bardziej zadowalające:
- Równanie ruchu (podane niżej) stosuje się bez modyfikacji, chociaż istnieją pewne przybliżenia.
- Mechanizm oddziałujący zegara wyjasnony jest jako rezonans okresowej siatki krystalicznej z rotacyjnym elektrycznym dipolem elektronu.
- Wyliczona szerokość najniższego rezonansu zgadza się z danymi.
- Rozbiezność pomiędzy zmierzoną a przewidywaną energią rezonansu wyjaśniona jest przez pozorne przesunięcie w maksimum, na skutek nierozwiązanego dubletu.
- Pomiar spodziewanych efektów spinowych wymaga większej rozdzielczości.
Szczegóły analizy analizy teoretycznej dostepne są w [3], a raport Gouanère’a został w końcu opublikowany w [4]. Główna niepewnosć eksperymentalna spowodowana jest ograniczonymi warunkami, w jakich przeprowadzono eksperyment. Zaobserwowany rezonans nie był przewidywany i wierzę, że nie można go wytłumaczyć standardową mechaniką kwantową. Zatem ruch drgający jest nieodłączny od równania Diraca, które nie może wyjaśnić rezonansu bez pewnych teoretycznych modyfikacji, które opisano niżej. Z pewnością pionierski eksperyment Gouanère’a powinien być usprawniony i powtórzony w celu potwierdzenia wyników i sprawdzenia nowych przewidywań! Gouanère obecnie za tym lobbuje.
Model dgrający elektronu
Schroedinger [5] ukuł termin zitterbewegung (ruch drgający) do opisania oscylacji w cząstkach swobodnych rozwiązania rownania Diraca. Jego domniemana fizyczna interpretacja została janso opisana przez Huang’a [6]:
Dobrze znany ruch drgający może być postrzegany jako ruch kołowy wokół kierunku spinu elektronu, o promieniu równemu długości Comptona elektronu razy 2π. Wewnętrzny spin elektronu można postrzegać jako orbitalny moment kątowy tego ruchu. Prąd, wytwarzany przez ten ruch drgajacy powoduje powstanie wewnętrznego momentu magnetycznego elektronu.
Sam Dirac zgadzał się z tą interpretacją [7]. Bez wątpienia autorytet Diraca miał wpływ na powtarzanie się jej w podręcznikach po dziś dzień, mimo, że nie poddane tego ani jednemu testowi eksperymentalnemu. W rzeczy samej, koncepcję ruchu drgającego przedstawiano jako nic ponad metaforę abstrakcyjnego formalizmu, podczas, gdy jej oszałamiające konsekwencje teoretyczne pozostawały niesprawdzone!!
Pozwolę sobie jawnie wypunktować literalne implikacje koncepcji ruchu drgającego:
- Równanie Diraca dostarcza statystycznego opisu zachowania elektronu z leżącą poniżej substrukturą cząstki.
- Elektron jest punktowym ładunkiem, poruszającym się z prędkością światła w ruchu kołowym o momencie kątowym wielkości ħ / 2, obserwowanym jako spin elektronu.
- Faza funkcji falowej Diraca jest miarą kątowego odchylenia w ruchu kołowym (zatem spin elektronu i faza są nierozerwalnie połączone!).
- Ruch kołowy powoduje obserwowalny moment magnetyczny elektronu.
- Ruch kołowy powoduje również pole dipola elektrycznego, o fluktuacjach na częstotliwości ruchu drgającego, rzędu 1021Hz.
W [2] i wszędzie indziej postuluję zaadoptowanie tych pięciu twierdzeń (w takiej czy innej formie) jako zasad zasad dla interpretacji ruchu drgającego w mechanice kwantowej. Brane dosłownie, proszą się one o konkretny model substruktury cząstki, która daje się sprawdzić ilościowo metodą eksperymentalną, oraz jest kompatybilna z ustanowionym już sukcesem mechaniki kwantowej. Dążyłem do tego celu przez dekady, tylko niedawno z wyraźnym postępem [3], po pokonaniu trwającego od dawna błędu na temat spinu elektronu. Wynikowy model przeszedł już empiryczny test eksperymentu zegarowego Gouanère’a. Teraz pozwólcie mi zaprezentować szczegóły projektu modelu, z naciskiem na rolę czasu.
Celem moich badań było utworzenie cząstkowego modelu elektronu, który obejmowałby w sposób zasadniczy spin i ruch drgający z równania Diraca, jak to wypunktowano powyżej. Ponieważ model rozszerza oryginalną koncepcję Schroedingera, a zitterbewegung
jest takim ochłapem, w odniesieniu do modelu używam słowa drgania (zitter). Zatem nowy model cząstki nazywam drgającym modelem elektronu, lub drgającym elektronem.
Jak radził Einstein, model powinien być tak prosty, jak to możliwe – ale nie prostszy!
Ponieważ prostota i przejrzystość teorii fizycznej silnie zależą od użytego formalizmu matematycznego, prezentuję model pozbawionym współrzędnych modelu algebry geometrycznej [8, 9], która gra kluczową rolę w jego rozwoju [3]. Nie spodziewam się, aby czytelnicy byli biegli w tym języku, wierzę jednak, że będzie on wystarczająco znajomy, aby dać jasne wyobrażenie na temat struktury modelu, co jest moim celem. Dla czytelników, którym to nie wystarcza, dołączam dodatek tłumaczący kluczowe wyrażenia na standardowy język tensorów.
Modelujemy elektron jako cząstkę punktową w czasoprzestrzeni z podobną od światła historią z = z(τ), zatem jej prędkość
- jest pustym wektorem: .
- (6)
Ponieważ właściwy czas nie może być zdefiniowany na krzywej świetlnej, fizyczna definicja parametru czasowego τ musi być określona innymi własnościamim modelu. Zobaczymy, że wewnętrzna definicja czasu elektronu pochodzi z założenia, że elektron posiada wewnętrzny moment kątowy lub spin. Spin S = S(τ) jest dwu-wektorem (zobacz dodatek, aby zobaczyć jego formę tensorową). Aby model był wewnętrznie spójny, okazuje się, że spin musi być pustym dwu-wektorem, wyrażonym jako:
- , .
- (7)
Cząstka jest naładowana, zatem oddziałuje z zewnętrznym polem elektromagnetycznym F = F(z).
Dynamika cząstki opisana jest szeregiem zespolonych równań ruchu dla prędkości u, pędu p oraz spinu S:
- , >dt>(8)
- ,
- (9)
- ,
- (10)
gdzie wektor promienia drgań, r zdefiniowany jest jako
- ,
- (11)
a potencjał drgań spinu zdefiniowany jest jako
- .
- (12)
Oznaczmy jednostki c = 1 a dwie stałe oddziaływania: ładunek q a stosunek ładunku do masy q/me, gdzie me jest masą spoczynkową elektronu.
Równania dynamiki mają całkę ruchu
- ,
- (13)
co definiuje masę m jako wielkość dynamiczną. Zatem potencjał Φ determinuje przesunięcie masy na skutek oddziaływania. Ponieważ pęd p jest wektorem czasowym (p2 > 0), w sposób konieczny jest nie-kolinearny ze świetlną prędkością u, a część pędu zawarta jest w S. Oczywiście, relacja pomiędzy p a S zdeterminowana jest dynamiką.
Samo-spójność tych trzech równań dynamicznych osiągnięto wyprowadzając je z lagranżjanu [3]. Wypływa z tego ważna lekcja: równania, jak (9) i (10) były proponowane i badane przez wielu autorów, szczególnie Corbena [10]. Jednakże, w analogii do teorii Diraca, Corben założył, że prędkość cząstki u, jak prąd Diraca, jest wektorem czasowym, oraz, że również spin jest dwu-wektorem przestrzennym o wartości |S| = ħ / 2. Argumentując, że prąd Diraca powinien być traktowany jako średni prąd świetlny w okresie drgania [2], przez lata próbowałem nieskutecznie zdefiniować model światło-podobnej cząstki o przestrzennym spinie. Stan ten trwał, aż nie spojrzałem na zapomnianą pracę Weyssenhoffa [11], kiedy zrozumiałem, że światło-podobna cząstka musi posiadać światło-podobny spin. Jednakże Weyssenhoff odnosił się tylko do cząstki swobodnej i nie było oczywiste, jak uogólnić to do cząstki oddziałującej. Samo-spójny system równań (6) do (12) udało mi się uzyskać tylko dzięki formule lagranżjanu. Swoją drogą, pokazało to, dlaczego model ze światło-podobną prędkością i przestrzennym spinem jest niemożliwy.
Drgający zegar elektronu
Teraz jesteśmy przygotowani do przeegzaminowania mechanizmu zegara w modelu drgającym. W równaniu ruchu cząstki (8), ostatni wyraz po prawej jest zwykłą siłą Lorentza, podczas, gdy pierwszy pisuje wewnętrzną krzywiznę o wektorze promienia r = r(τ). Z (11) wynika, że r ⋅ u = r ⋅ p = 0, a promień krzywizny elektronu można zdefiniować przez
- (14)
Centrum krzywizny x = x(τ) można zdefiniować jako
- .
- (15)
Jest to czaso-podobna krzywa z prędkością v=x⋅, zatem jej długość łuku definiuje czas właściwy τ, ktory może być uzyty jako parametr czasowy w naszym modelu. Tym razem parametr jest zewnętrznie powiązany z geometrią czasoprzestrzeni, dostarcza zatem połączenia z wewnętrzną geometrią ruchu elektronu.
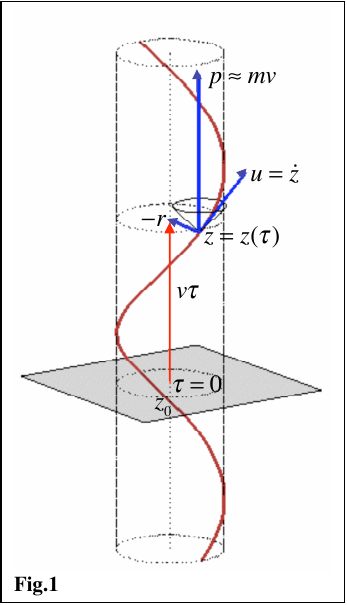
Dla cząstki swobodnej (F = 0), równania ruchu elektronu mogą być dokładnie scałkowane. Jak zilustrowano na Fig. 1, rozwiązaniem z = z(τ) jest światło-podobna helisa, wyśrodkowana na prostą, czaso-podobną linię kolinearną z pędem p. Ogólne rozwiązanie można przedstawić jako deformację tej helisy poprzez oddziaływanie z zewnętrznym polem elektromagnetycznym. Konkretniej, można można je opisać następująco:
Prędkość v = v(τ) definiuje momentalny, spoczywający układ odniesienia dla elektronu. W układzie tym orbitę elektronu można przedstawić jako poruszanie się z prędkością światła po kole o wektorze promienia r(τ) wokół ustalonego punktu x(τ). Zgodnie z (14), promień i częstotliwość drgań jest odwrotnie powiązane poprzez
- ,
- (16)
gdzie indeksy oznaczają wartości cząstki swobodnej. Z (13) wynika, że częstotliwości są powiązane wzorem
- .
- (17)
To pokazuje, jak częstotliwość i promień drgań zmienia się wraz z oddziaływaniem. Gdy na skutek oddziaływania zwiększa się masa, rośnie częstotliwość a promień zmniejsza się, aby zachować prędkość światła.
Skala wewnętrznego czasu i długości elektronu zdeterminowana jest przez wartości cząstki swobodnej. Częstotliwość drgań wynosi około jednego Zeta (1021) Hz, a mówiąc dokładniej, jest podwójną częstotliwością de Broglie w (3):
- .
- (18)
Odpowiednio, podstawowa jednostka czasu elektronu, Te, wynosi około 4 zepto (10-21) sekund;
- .
- (19)
Podstawową jednoską długoci jest promień drgania (lub spinu):
- ,
- (20)
gdzie λc jest długością Comptona elektronu.
Kątowe odkształcenie cyrkulacji drgań,
- (21)
dostarcza wewnętrznego pomiaru czasu zegara elektronu, niezależnego od jednostek fizycznych. Kąt φ jest analogiczny do fazy w funkcji falowej Diraca.
Odczytanie zegara elektornu wymaga analizy oddziaływania spin-drgania. Fizyczna struktura tej interakcji jest najbardziej widoczna w relacji do momentalnego układu spoczynkowego elektronu. Jak w pełni wyjaśniono to w [3], algebra geometryczna umożliwia dekompozycję układu spoczynkowego spinu i pola elektromagnetycznego do prostej fomry zespolonej:
- , .
- (22)
Wektory A i B są, oczywiście, polami elektrycznym i magnetycznym w układzie spoczywającym. Wektor spinu s jest właściwie niezmiennikiem, zdefiniowanym jako uśrednienie dwu-wektora spinu S po okresie drgania. Mamy zatem
- , z magnitudą ,
- (23)
jest w dokładnej zgodzie z teorią Diraca. Wektor promienia drgań re posiada ustaloną wielkość |re| = λe. Teraz oddziaływanie spin-drganie może być wyrażone w zrozumiałej formie
- (24)
Ostatnim elementem w (24) jest znane oddziaływanie Zeemana, z poprawnym stosunkiem żyromagnetycznym (g = 2), przewidzianym przez teorię Diraca. Wstawiając to do równania pędu (9), widzimy, że daje to siłę Sterna-Gerlacha, gdy pole magnetyczne jest niejednorodne.
Innym czynnikiem w (24) jest interakcja dipola elektrycznego z momentem dipolowym d = −qre, obracającego się wokół osi spinu s z częstotliwością drgania. Term ten uśrednia się do zera na przestrzeni okresu drgania, o ile pole E również nie oscyluje z porównywalną częstotliwością, powodując rezonans z dipolem. W taki sposób model drgający wyjaśnia oddziaływanie pomiędzy zegarem elektronu a siatką krystaliczną w eksperymencie z tunelowaniem.
Można teraz następująco podsumować podstawowe właściwości modelu drgań:
- Historią czasoprzestrzenną elektronu jest światło-podobna helisa.
- Masa elektronu (≈ częstotliwość drgań) jest miarą krzywizny helisy.
- Faza elektronu (≈ kąt drgania) jest miarą rotacji na helisie.
- Drgania elektronu generują statyczny dipol magnetyczny oraz obrotowy dipol elektryczny!
Wszystko to pasuje razem do prostego obrazu pracy mechanizmu zegara elektronu:
Ruch elektronu sterowany jest przez spin S, który ogranicza jego historię w czasoprzestrzeni na powierzchni czaso-podobnej tuby drgań, równoległej do pędu p. Pęd determinuje wewnętrzna dekompozycję spinu (22) na część przestrzenną is, określającą przekrój tuby, oraz część temporalną mr, określającą temporalną intensywność [pitch] helisy. Jako, że stanowi to trzon modelu drgającego, nazwijmy to mechanizmem spinowo-drgającym.
Teraz możemy opisać interakcje z zewnętrznym polem elektromagnetycznym jako deformację tuby drgań, a to otwiera możliwości do uogólniania na inne cząstki i oddziaływania, jak to zasugerowano poniżej.
Uniwersalność drgań
Kiedy zapytano Einsteina, dlaczego zignorował ekscytujące odkrycia nowych cząstek elementarnych
, odparł
Wiesz, wystarczyłoby na prawdę zrozumieć elektron!
W rzeczy samej, teoria elektronu jest warsztatem, na którym zaprojektowano, zbudowano i przetestowano teorię kwantową. Zatem to, co jest fundamentalnie prawdziwe dla elektronu, prawdopodobnie jest prawdziwe dla wszystkich fermionów i jest dziedziczone przez bozony, będące kompozytami fermionów. Pozwolę sobie pospekulować nad implikacjami tego stwierdzenia pod kątem uniwersalności mechanizmu drgająco-spinowego. Na prowadzenie wyłaniają się trzy główne kwestie.
Pierwszą jest potwierdzenie modelu, dzięki któremu możemy być pewni, że drgania są fundamentalną właściwością elektronu. Jak dotąd miał miejsce tylko eksperyment zegarowy z tunelowaniem, potrzeba powtórzeń, aby być pewnym wyników. Jednakże, powody przeoczenia drgań przez tak długi czas są oczywiste. Ponieważ częstotliwość drgań jest tak wysoka, ich efekt uśrednia się do zera w większości sytuacji, i można go zaobserwować tylko w warunkach rezonansu. Rezonans drgań może być całkiem powszechny. W [3] twierdziłem, że wyjaśnia on wiele unikalnych własności mechaniki kwantowej. Co więcej, subtelne odchylenia od standardowej mechaniki kwantowej są przewidziane przez drgający dipol.
Drugą sprawą jest kompatybilność z mechanik kwantową. Ponieważ spon i temporalne drgania są już obecne w równaniu Diraca, kompletny mechanizm drgająco-spinowy można zastosować poprzez zastąpienie czasowego prądu Diraca prądem świetlnym [3]. Prąd Diraca można odzyskać uśredniając po okresie drgań. Wydaje się prawdopodobne, że wynikowe równanie drgające Diraca jest wystarczająco podobne od oryginału, aby odtworzyć potwierdzone empirycznie wyniki, takie, jak widmo atomu wodoru. Główną różnicą jest istnienie drgającego dipola elektrycznego, w doskonałej analogii modelu drgającego cząstki. Do ustalenia pozostają różnice w przewidywaniach miedzy modelem drgającym Diraca, a cząsteczkowym modelem drgającym. model cząsteczkowy ma tą przewagę, że posiada jasną interpretację fizyczną i prostotę w zastosowaniach. Równanie drgające Diraca ma zaś tą przewagę, że można do niego stosować wszystkie standardowe metody mechaniki kwantowej i kwantowej teorii pola.
Na koniec warto wspomnieć, że koncepcja drgań posiada implikacje co do interpretacji nierelatywistycznego równania Scroedingera. Jego wyprowadzenie z równania Diraca pokazuje, że przestrzenna część spinu (22) jest pomijana, podczas, gdy część czasowa jest zachowywana w czynniku fazowym funkcji falowej, przez co czynniki masy spoczynkowej są zbijane razem. Można zatem wywnioskować, że faza funkcji falowej Schroedingera opisuje przesunięcie fazy drgań.
Idąc w bardziej spekulatywnym kierunku, równanie drgające Diraca posiada zaskakujące implikacje dla teorii oddziaływań elektro-słabych [3, 12]. Wykorzystuje ono tylko dwa z czterech komponentów spinora Diraca, do wykorzystania są więc jeszcze dwa. Istnieją dwie ważne kwestie przy dokonywaniu wyboru. Po pierwsze, generatorem cechowania transformacji elektromagnetycznych w równaniu Diraca jest dwu-wektor czasoprzestrzenny, zatem jest to powiązane z geometrią czasoprzestrzeni. Po drugie, Maksymalną grupą symetrii pełnego równania Diraca dokładnie grupa SU(2)×U(1) oddziaływań elektro-słabych. W konsekwencji, jeżeli identyfikujemy rezydentną część funkcji falowej Diraca z neutrino elektronowym, mamy pełne geometryczne zagnieżdżenie oddziaływań elektro-słabych, zatem cała funkcja reprezentuje dublet leptonowy. Włączenie oddziaływań elektrosłabych jest więc w linii prostej [3, 12]. Pojawiają się jednak dwie zasadnicze różnice. Po pierwsze, równanie drgające Diraca jest raczej typu Majorany niż Weyla. Po drugie, dla elektronu potrzebne są tylko lewe komponenty, ponieważ prąd ładunku jest świetlny. Wygląda na to, że elementy po prawej są w standardowej teorii potrzebne jedynie do uczynienia strumienia ładunku czasowym. Ewidentnie ta wersja teorii oddziaływań elektrosłabych zasługuje na poważne potraktowanie, jeżeli brać poważnie mechanizm drgający spinu.
Jeżeli mechanizm drgającego spinu jest uniwersalny dla elementarnych fermionów, musi być mnożony przez pewne mechanizmy determinujące widmo masy spoczynkowej (częstotliwości drgań). Wydaje się wątpliwe, czy mechanizm Higgsa mógłby do tego posłużyć, lecz jest to kwestia otwarta. Być może wskazówka znajduje się poniżej.
Trzecią kwestią jest kompatybilność z ogólną teorią względności.
Einstein nigdy nie był zadowolony ze źródła pola grawitacyjnego w postaci pędu-energii w swoim równaniu, ewidentnie ze względu na jego niegeometryczny charakter. Hipoteza drgań spinowych może poprawić tą niedogodność, gdyż redukuje masę spoczynkową do geometrycznej częstotliwości w krzywiźnie światło-podobnej trajektorii cząstki. Powstaje oczywiste pytanie: W jaki sposób ma się to do masy grawitacyjnej i pola grawitacyjnego?
Pozwólmy sobie na rozważenie paru możliwości bez podawania ostatecznej odpowiedzi.
Być może masa spoczynkowa pochodzi z oddziaływań grawitacyjnych. Rosquist [13] podkreślił, że standardowy argument nieistotności oddziaływań grawitacyjnych w skali Comptona jest poważnie wadliwy, gdyż oparty jest na koncepcjach newtonowskich. Argumentował za to za rozwiązaniem Kerra-Newmana dla równań Einsteina-Maxwella, gdyż jest to najbliższa rzecz w modelu ogólnej teorii względności do modelu elektronu z ładunkiem i spinem. Wywnioskował z tego, że oddziaływania grawitacyjne i elektromagnetyczne są porównywalne w skali promienia spinu [20]. Te prowokacyjne wnioski rzucają nam wyzwanie do rozszerzenia modelu drgań spinowych na samoodziaływanie grawitacyjno-elektromagnetyczne w zgodzie z zasadami ogólnej teorii względności – co jest trudną sprawą.
Hipoteza drgań spinowych posiada implikacje zarówno dla pól grawitacyjnych, jak i dla ich źródeł. Mówi nam, że nie ma masy bez spinu. Zatem równania pola grawitacyjnego muszą zostać rozszerzone o spin. Uczyniono to w Teorii Grawitacji z Cechowaniem [9, 12], która zakłada, że źródła są opisane równaniem Diraca i wskazuje, że spin powoduje powstanie wiru w polu grawitacyjnym. Warto byłoby zrewidować tą teorię celem ustalenia modyfikacji spowodowanych pustymi dwu-wektorami spinu, czego wymaga hipoteza drgań spinowych.
Wydaje się, że dyskusja na temat natury czasu nie jest obecnie kompletna bez pewnych znacznych ekstrapolacji dla kosmicznych konsekwencji. Ciemna Materia jest popularnym celem! Pozwólcie mi więc zaproponować rozwiązanie na czasie: wiemy na przykład, że nagromadzona siła grawitacyjna z gwiazd jest niewystarczająca do wytłumaczenia momentu kątowego galaktyki. Być może niezgodność nie występuje na skutek brakującej materii, lecz brakującego momentu kątowego w polu grawitacyjnym, którego może dostarczyć komponent wirowy. Faktycznie bowiem, hipoteza drgań spinowych wymaga, a by masa była cząstek była związana ze spinem. Być może wir grawitacyjny, wywołany spinem, podobnie, jak siła grawitacji spowodowana masą, jest zaniedbywalny na poziomie atomowym, ale w skali galaktyki gromadzi się do zauważalnego poziomu. Tyle w temacie!
Teraz jest czas, aby przerwać spekulacje, zanim reputacja hipotezy drgań spinowych nie będzie poważnie skompromitowana!
Dodatek
Oto kilka odpowiedników pomiędzy wyrażeniami w algebrze geometrycznej a ich formami w standardowym rachunku wektorowym:
,
,
,
,
.
Odnośniki
[1] L. de Broglie (1923), Ondes et Quanta, Comptes Rendus 177: 507-510.
[2] D. Hestenes (1990), The Zitterbewegung Interpretation of Quantum Mechanics, Foundations of Physics 20: 1213-1232.
[3] D. Hestenes (2008), Zitterbewegung in Quantum Mechanics –– a research program, arXiv:8002.2728 v1 [quant-ph].
[4] M. Gouanère et. al. (2008), A Search for the de Broglie Particle Internal Clock by Means of Electron Channeling, Foundations of Physics 38: 659-664.
[5] E. Schroedinger (1930), Uber die Kraftfreie Bewegung in der Relativistischen Quantenmechanik, Sitzungb. Preuss. Akad. Wiss. Phys.-Math. Kl. 24: 418.
[6] K. Huang (1949), On the zitterbewegung of the electron, Am. J. Phys. 20: 479.
[7] P. A. M. Dirac (1957), The Principles of Quantum Mechanics, (Oxford U. Press: Oxford, 4th edition), pp. 261-267.
[8] D. Hestenes (2003), Spacetime Physics with Geometric Algebra, Am. J. Phys. 71: 691-704.
[9] C. Doran & A. Lasenby (2002), Geometric Algebra for Physicists (Cambridge: The University Press).
[10] H. Corben (1948), Classical and Quantum Theory of Spinning Particles, (Holden-Day: San Francisco, 2nd edition). [11] J. Weyssenhoff (1947), On Two Relativistic Models of Dirac’s Electron, Acta Phys. Pol. 9: 47-53.
[12] D. Hestenes (2008), Gauge Gravity and Electroweak Theory. In H. Kleinert, R. T. Jantzen & R. Ruffini (Eds.), Proceedings of the Eleventh Marcel Grossmann Meeting on General Relativity (World Scientific, Singapore). See
[13] K. Rosquist (2004), Gravitationally Induced Electromagnetism at the Compton Scale, arXiv:gr-qc/0412064 v2 .
David Hestenes, Arizona State University
Przetłumaczono z: Electron time, mass and zitter, z portalu FQXi.
Przetłumaczył Łukasz Buczyński
Dzięki za wszystkie opublikowane tłumaczenia!Dobra robota, prima sort.
Dziękuję za komentarz. Kieruję się często intuicją, widać, że mam chyba dobrą 😉