4.1 Równanie pola elektromagnetycznego
Naukowcy próbują wyjaśnić fizyczne układy za pomocą modeli matematycznych, które opisują i przewidują zachowanie układu. Na przykład, Kepler opisał ruch planet przy pomocy trzech praw. Analogicznie, zachowanie plazmy jest determinowane przez równania pola elektromagnetycznego, które opisują ruch cząstek naładowanych oraz ich oddziaływanie z polem elektrycznym i magnetycznym. Istnieją dwa elementy równań pola elektromagnetycznego: równania Maxwella oraz równanie siły Lorentza. Te dwa komponenty działają razem w sprzężeniu zwrotnym:
Równania Maxwella określają pola elektryczne i magnetyczne w zależności od pozycji i ruchu ładunków elektrycznych. Opisują również oddziaływania pól elektrycznych i magnetycznych, jeżeli coś się zmienia.
Prawo siły Lorentza określa siłę wywieraną na cząstkę naładowaną, poruszającą się w polu elektromagnetycznym. Siła ta zmusza każdą cząstkę do ruchu, zgodnie z prawami Newtona. Zmiany w pozycji i ruchu naładowanych cząstek powodują zmiany pól elektrycznych i magnetycznych.
Stworzono programy komputerowe do naśladowania tego zachowania plazmy. Wykonują one zazwyczaj szereg kroków, z których każdy reprezentuje mały odcinek czasu. Najpierw na podstawie danych sił elektrycznych i magnetycznych oraz położenia, ruchu i masy naładowanych cząstek, obliczane są siły działające na każdą z nich, wynikające z prawa Lorentza. Na podstawie sił składowych wyliczany jest wynikowy wektor siły dla danej cząstki. Następnie oblicza się drogę, jaką pokonuje w czasie odpowiadającym jednej iteracji. Jest to powtarzane dla całego zbioru cząsteczek.
Następnie, na podstawie położenia i kinematyki cząstek, wyliczane są z równań Maxwella pola elektryczne i magnetyczne. Następnie program zaczyna nową pętlę, obliczając wpływ tych pól na każdą cząstkę przy użyciu prawa Lorentza.
Pętla powtarza się dotąd, aż spełniony zostanie jakiś warunek, np osiągnięta zostanie zadana liczba powtórzeń, albo któraś zmienna osiągnie lub przekroczy zadaną wartość etc.
Gdy tylko zdefiniuje się warunki początkowe (liczba cząstek, ich ładunki, masa, początkowe prędkości oraz intensywność pól magnetycznych i elektrycznych przenikających rozważaną przestrzeń), algorytm pętli można przedstawić następująco:
1. Oblicz wszystkie siły działające na każdą cząstkę przy użyciu prawa Lorentza
2. Oblicz nowe położenia i prędkości dla odcinka czasu przypadającego na pętlę, używając równania ruchu Newtona
3. Oblicz E i B dla każdej nowej pozycji cząstki, następnie zwiększ licznik czasu
4. Jeżeli nie jest spełniony warunek końca pętli, idź do punktu 1.
Dla lepszego realizmu można uwzględnić jeszcze inne aspekty, jak zderzenia cząstek, lepkość, grawitację etc. To złożone zagadnienie, a duże modele, z wieloma cząsteczkami, mogą pochłonąć miesiące pracy superkomputerów.
Sprzężenie zwrotne może gwałtownie doprowadzić do bardzo złożonych zachowań, które są niezwykle trudne do matematycznego opisu. Często stosuje się uproszczenia. Aczkolwiek owe uproszczenia często właśnie prowadzą do pominięcia tych zachowań plazmy, które odróżniają ją od gazy lub płynu.
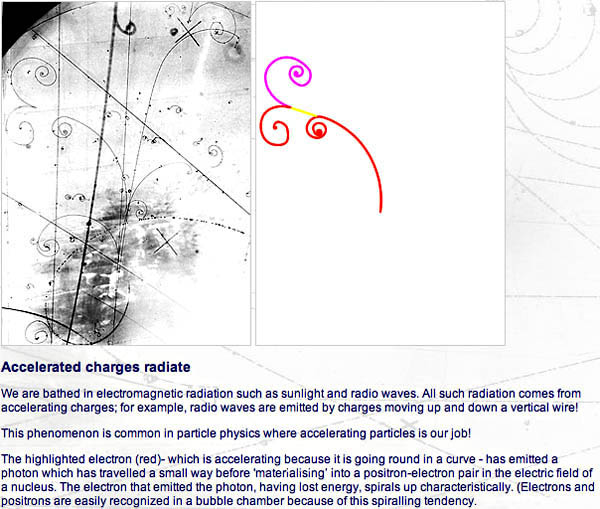
Przyspieszone ładunki promieniują
Jesteśmy skąpani w promieniowaniu elektromagnetycznym, takim jak światło Słońca czy fale radiowe. Wszystkie to promieniowanie pochodzi z przyspieszających ładunków; np. fale radiowe są emitowane przez ładunki poruszające się w górę i w dół przewodu elektrycznego!
Zjawisko to jest powszechne w fizyce cząstek elementarnych, gdzie przyspieszanie ładunków jest naszą pracą!
Zaznaczony elektron (czerwony) – który jest przyspieszany, ponieważ porusza się po krzywej – emituje foton, który przebywa niewielką odległość, zanim się „zmaterializuje”, tworząc parę „elektron-pozyton”, w polu elektrycznym jądra atomowego. Elektron, który wypromieniował foton, traci energię, co objawia się charakterystycznym spiralnym torem (elektrony i pozytrony są łatwo rozpoznawalne w komorze pęcherzykowej po swoich skłonnościach do ruchu spiralnego).
Komora pęcherzykowa, wypełniona pole magnetycznym, produkuje widoczne tory naładowanych cząstek, pozwalając ustalić ich energie, interakcje i składniki kolizyjne, gdy ostawione są w linii z akceleratorem cząstek. Obrazek i opis: Samouczek o komorze pęcherzykowej dostarczony przez CERN (link)
Pełny opis równań pola elektromagnetycznego znaleźć można w Załączniku II. Tutaj podsumujemy kluczowe punkty.
4.2 Równania Maxwella
Implikacje równań Maxwella oraz ich badań są następujące:
1. Statyczne pole elektryczne może istnieć bez pól magnetycznych. Kondensator lub cząsteczka pyłu o statycznym ładunku Q mają pole elektryczne, ale nie mają magnetycznego.
2. Stałe pole magnetyczne może istnieć bez elektrycznego. Przewodnik ze stałym prądem I posiada pole magnetyczne, ale nie posiada elektrycznego.
3. Tam, gdzie występuje zmienne pole elektryczne, musi również istnieć niezerowe pole magnetyczne.
4. Tam, gdzie istnieje zmienne pole magnetyczne, musi istnieć niezerowe pole elektryczne.
5. Bez stałego magnesu, pole magnetyczne może być utworzone tyko na dwa sposoby – przez prąd elektryczny, lub zmienne pole elektryczne.
6. Nie istnieją magnetyczne monopole. Wszystkie linie pola magnetycznego stanowią zamknięte pętle.
4.3 Prawo siły Lorentza
Siła orentza reprezentuje całkowitą siłę działającą na cząstkę, wynikającą z oddziaływania zarówno z polem elektrycznym, jak i magnetycznym. Wynikowa siła wymusza ruch cząstki zgodnie z mechaniką Newtona. Ponieważ prawo Lorentza jest fundamentalne dla zachowania się plazmy, warto zatem poświęcić trochę czasu na jego zrozumienie. Oto równanie:
F = Q(E + U × B)
(wektory zaznaczono pogrubieniem
gdzie F jest siłą Lorentza; Q jest ładunkiem cząstki, E jest intensywnością pola elektrycznego, U jest prędkością cząstki, B jest gęstością strumienia magnetycznego a × jest operatorem mnożenia wektorowego.
Aby zrozumieć znaczenie równania, trzeba mieć pewną wiedzę o wektorach.
Wektor to struktura posiadająca zarówno długość jak i kierunek. Przykładami mogą być tutaj prędkość czy siła. Jest jak strzałka. W odróżnieniu od niego, skalar posiada tylko jedną wartość. Przykładami są prędkość czy temperatura. Algebra wektorów to dział matematyki operujący na wektorach. Dla niecierpliwych, dodatkowe informacje są dostępne w załączniku III. Wyjaśnienie na Hiperfizyce również jest dobrym wprowadzeniem. Tutaj zostaną wyjaśnione podstawy potrzebne do zrozumienia równania Lorentza.
Po pierwsze, mnożenie wektora przez skalar jest jak odpowiednie zwielokrotnienie strzałki. Wektor jest pierwszą strzałką, skalar określa ich całkowitą liczbę. Rezultatem jest dłuższa strzałka skierowana w tym samym kierunku, co oryginalny wektor.
Uproszczonym przykładem jest zwiększanie prędkości samochodu jadącego po linii prostej. Można sobie wyobrazić wektor prędkości samochodu skierowany równo z drogą, a zaczynający się zawsze dokładnie pośrodku samochodu. Załóżmy, że strzałka ta ma 20 cm długości, co reprezentuje prędkość 20 km/h. Następnie wciskamy pedał gazu i zwiększamy prędkość. W miarę, jak prędkość samochodu rośnie, długość strzałki zwiększa się, zawsze odpowiadając prędkości. Przy 60 km/h jej długość wynosi 60 cm, i wciąż jest skierowana równolegle do drogi. Gdy wciśniesz pedał hamulca, samochód zacznie przyspieszać w przeciwnym kierunku, zwalniając, a strzałka będzie coraz krótsza i krótsza. Gdy samochód się zatrzyma, prędkość będzie zerowa, i długość strzałki również będzie zerowa.
Powiesz: „To łatwe do pojęcia. A co będzie, jeśli skręcę kierownicą, powiedzmy, w prawo?” Taka akcja wprowadza dodatkową siłę działającą na samochód, skierowaną w innym kierunku niż do przodu. Nie zmieni ona jego prędkości (pomijamy tarcie!), jedna coś się zmieniło, ponieważ samochód skręca. Wektor prędkości, wskazujący 60 km/h nie zmienił swojej długości, ale pojawiła się dodatkowa siła z innego kierunku, więc teraz wektor prędkości jest rezultatem dwóch sił (dwóch strzałek działających na środek samochodu). Tak długo, jak trzymasz kierownicę skręconą pod tym samym kątem, będzie działała taka sama siła, próbująca obrócić samochód, tak, że będzie on jeździł w kółko ze stałą prędkością.
Widzimy więc, że mamy tutaj dwa rodzaje przyspieszenia: zmiany w prędkości ruchu, szybciej lub wolniej – czyli zwykłą wartość numeryczną zmiany odległości w jednostce czasu bez związku z jakimkolwiek kierunkiem – oraz zmiany kierunku ruchu – zmiana kąta kierunku, na który coś wskazuje, bez odniesienia, jak szybko to coś się porusza wzdłuż tego kierunku. Obydwa typy zmian dają siłę przyłożoną do obiektu.
Mnożenie przez siebie dwóch wektorów jest nieco bardziej skomplikowane. Pomyśl o dużej śrubie w drewnianej płycie, gdzie rowek w główce reprezentuje pierwszy wektor, a drugi wektor jest narysowany na płycie. Gdy śruba jest przekręcana zgodnie z ruchem wskazówek zegara, dopóki rowek nie zrówna się z drugim wektorem, zagłębia się ona w drewnie. Głębokość wkręcenia zależy od wielkości i skoku śruby, oraz kąta wkręcenia. Iloczyn wektorowy jest właśnie czymś mniej więcej takim.
Mnożenie dwóch wektorów używają iloczynu wektorowego powoduje powstanie wektora prostopadłego do płaszczyzny zawierającej pierwsze dwa wektory. Kierunek nowego wektora dany jest kierunkiem obrotów naszej wyimaginowanej śruby. Długość wynikowego wektora zależy zarówno od kąta pomiędzy wektorami wejściowymi, jak i od ich długości.
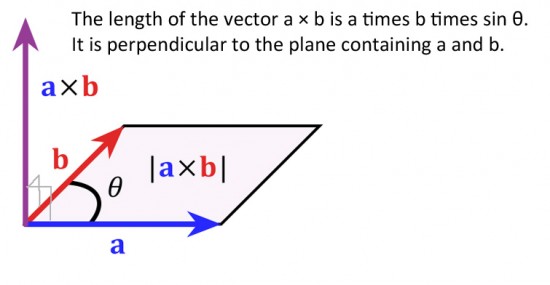
Długość wektora a × b wynosi a · b · sin θ.
Jest on prostopadły do płaszczyzny zawierającej a i b.
Tak jak było w przypadku naszej śruby, jeśli wektory są równoległe, nie ma miejsca obrót, a iloczyn wektorowy jest zerowy.
Bardziej formalnie, jeśli w kartezjańskim układzie współrzędnych wektor w kierunku x jest mnożony przez wektor w kierunku y, rezultatem jest wektor w kierunku z. Długością wynikowego wektora jest potrójny iloczyn długości obydwu wektorów i sinusa mniejszego kąta pomiędzy nimi. Gdy wektory są równoległe, kąt pomiędzy nimi jest zerowy. Sinus z zerowego kąta również jest zerowy, więc w tym przypadku nie ma wynikowej siły w kierunku z.
Efekt ten jest bardzo podobny do efektu żyroskopowego w obracającym się ciele stałym: siła przyłożona w jednym kierunku skutkuje w ruchu w kierunku prostopadłym. Jest to zwane precesją.
Wracając do prawa Lorentza, widzimy, że całkowita siła składa się z dwóch części. Pierwszą jest QE, która jest iloczynem skalarnego ładunku i wektora pola elektrycznego.
Zauważmy, że siła wywołana przez pole E jest stała i równoległa do pola, co skutkuje stałym przyspieszeniem cząstki wzdłuż pola, zgodnie z prawem Newtona – w jednym kierunku dla ładunków dodatnich, w drugim dla ujemnych.
Druga część równania, Q(U × B), jest bardziej interesująca. Mamy tu iloczyn dwóch wektorów, mnożony następnie przez skalarny ładunek cząstki. Zakładając, że cząstka nie poruszała się wzdłuż linii pola, pojawi się siłą prostopadła zarówno do toru cząstki, jak i do linii pola. To wyjaśnienie zasady prawej dłoni wyjaśnia siłę „sterującą”, wywieraną w określonym kierunku przez pole magnetyczne na naładowaną cząstkę, która wchodzi w owo pole.
Siła prostopadła do kierunku ruchu jest siłą dośrodkową. Pole magnetyczne będzie więc powodować poruszanie się cząstki po kolistym torze, w płaszczyźnie prostopadłej do linii pola. Podczas ruchu po takim torze prędkość cząstki ciągle posiada komponent prostopadły do linii pola, więc ciągle działa na nią siła prostopadła do ruchu. Jej kierunek wciąż się zmienia, ale prędkość skalarna pozostaje stała.
Prostym przypadkiem jest rozważenie co się stanie, gdy grupa cząstek wkroczy w nieruchome pole magnetyczne. Dla uproszczenia pominiemy wszelki wpływ tych cząstek na pole. Jeśli wlecą w pole równolegle do jego linii, nie doświadczą żadnej siły, i zmieni się ich kierunek ani prędkość. Gdy wlecą w pole prostopadle do jego kierunku, zaczną zataczać zamknięte koła.
Bez pola elektrycznego, prawo Lorentza przedstawia siłę dośrodkową – F = Q(U × B). Siła przyłożona do cząstki jest wprost proporcjonalna do Q – ładunku cząstki, do U – jej prędkości, oraz do B – wektora pola magnetycznego. U × B oznacza U razy B razy sin mniejszego kąta pomiędzy wektorami. To oznacza, że UB jest mnożone przez sin kąta, więc jego efekt ma zasięg od zera do 1. Na porównawczej ilustracji poniżej, ładunek cząstek i pole magnetyczne pozostają niezmienne, podczas gdy prędkość cząstek, gdy wkraczają w pole, zwiększa się od lewej ku prawej. Im szybciej cząstka się porusza, tym większy okrąg zakreśla, ponieważ jego promień r jest miarą momentu liniowego mU cząstki, gdzie m jest jej masą: r = mU ÷ (|Q|B). Ten sam rezultat osiągnie się zmniejszając ładunek, przy zachowaniu pozostałych dwóch zmiennych.
Gdy cząstka wchodzi w pole magnetyczne pod kątem, ze składową prędkości równoległą do linii sił pola, będzie „dryfować” w kierunku wzdłuż linii pola podczas swojego ruchu kołowego. Tor jej lotu będzie kreślił spiralę. Promień r jest znany jako promień Larmora lub promień cyklotronowy. Na trzech ilustracjach u dołu, kąt wejścia cząstki w pole oraz wektor pola B pozostaje taki sam. Natomiast prędkość wejścia cząstki w pole zwiększa się od lewej ku prawej, żeby pokazać, że im szybciej cząstka się porusza, tym większe kreśli okręgi.
Na trzech rysunkach poniżej, zielony wektor wejścia pokazuje, którą drogą będzie się poruszał ładunek dodatni (przez konwencję). Cząstka może się poruszać w obydwa kierunki wzdłuż tego wektora, więc jak zobaczymy, istnieją dwie trajektorie wychodzące z czubka wektora. Jeśli cząstka będzie ujemna, będzie przyspieszać w przeciwnym kierunku, a gdyby była cięższa lub miała większą prędkość, zataczałaby większe kręgi. Podobnie, gdyby zmieniło się pole elektryczne albo magnetyczne, przy zachowaniu innych czynników bez zmian, w podobny sposób zmieniłoby to tor ruchu cząstki. Wąskie pomarańczowe „tuby” trajektorię cząstki w zależności od warunków wejścia.
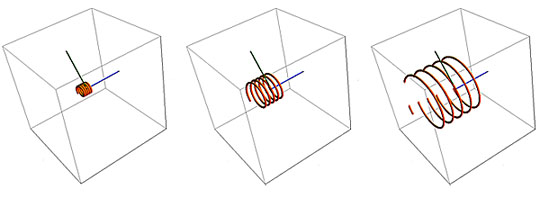
Gdy naładowana cząstka wkracza w jednorodne pole magnetyczne B, jej tor jest zaginany w okrąg o promieniu r proporcjonalnym do momentu liniowego, masy pomnożonej przez prędkość (mU). Prędkość cząstki się nie zmienia, podobnie jak jej energia kinetyczna a pole nie wykonuje pracy na cząstce. Jest to podobne do pola grawitacyjnego, oddziałującego ciągłą siłą dośrodkową na satelitę okrążającego Ziemię. Kierunek pola magnetycznego pokazany jest niebieską linią w osi toru cząstki. Wektor wlotu cząstki zaznaczono na czerwono linią radialną.
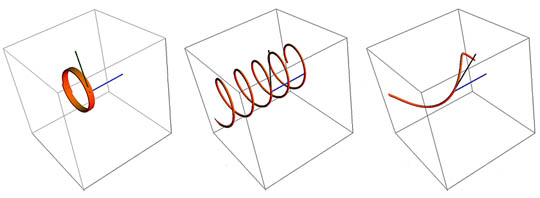
Gdy kąt wejścia cząstki w pole zmienia się z prostopadłego na równoległy, jej trajektoria zmienia się w coraz bardziej rozciągniętą spiralę. Zwróć uwagę na zmiany kąta zielonego wektora wlotu i helikalny skręt. Ilustracje powyżej powstały przy użyciu Mathematica Demonstration.
Całkowita siła będzie wynikowym wektorem sił elektrycznych i magnetycznych oraz będzie zależeć od kąta pomiędzy nimi (ilustracje poniżej).
Jeśli pola elektryczne i magnetyczne są równoległe (jak w przypadku prądu przyległego do pola, który rozważymy później), wówczas naładowana cząstka, wchodząca radialnie w kierunku osiowym pól będzie zmuszona podążać helikalną ścieżką wzdłuż pola. Będzie przyspieszać (stale zmieniać kierunek w spirali idącej wzdłuż pola magnetycznego)na skutek prawa Lorentza, oraz jednocześnie przyspieszać (zmieniać prędkość skalarną) w kierunku pola elektrycznego.
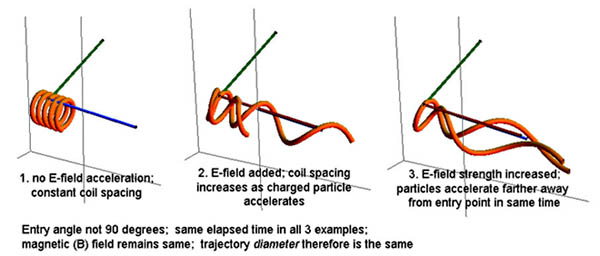
W sytuacji przylegania pól (E i B są równoległe), cząstka doświadcza siły dośrodkowej z pola magnetycznego, a jednocześnie pole elektryczne E zmusza ją do przyspieszania wzdłuż osi pola. Z czasem cząstka porusza się niemal równolegle do pola.
Jeśli cząstka wkroczy w układ równoległych pól osiowo, nie doświadczy oddziaływania pola magnetycznego. Aczkolwiek pole elektryczne będzie ją wciąż przyspieszać wzdłuż linii pola. W zależności od ładunku, gdy cząstka wkroczy w taki region, jej prędkość wzrośnie. Jeśli wkroczy w pole z przeciwnej strony, będzie zwalniać, zatrzyma się, po czym zacznie przyspieszać w przeciwnym kierunku. „Kierunkiem” pola elektrycznego nazywamy kierunek siły działającej na położony w nim ładunek dodatni.
Gdy pola nie są równoległe, mogą wystąpić różne kombinacje trajektorii, w zależności od ładunku, natężenia pola, kierunku wejścia cząstki i kąta nachylenia pomiędzy kierunkiem pól.
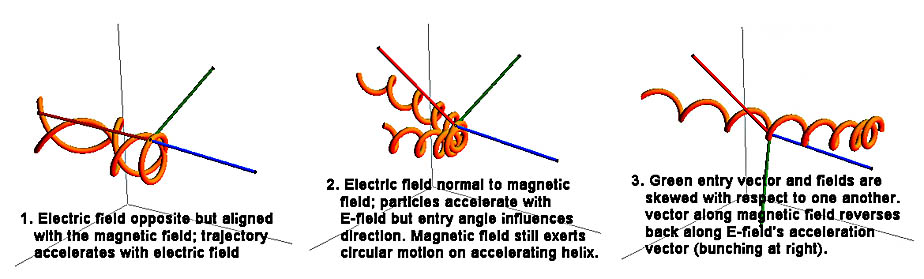
Przy stałym polu elektrycznym, cząstki będą zwiększały prędkość wzdłuż linii pola elektrycznego. Ilustracje powstały przy pomocy Mathematica Demonstration.
Aczkolwiek owe trajektorie mogą wyglądać skomplikowanie, reprezentują tylko jedną naładowaną cząstkę na raz, o stałej prędkości, ze stałymi polami elektrycznym i magnetycznym. W praktyce ten sam region mogą zajmować cząstki o różnej polaryzacji i wektorach prędkości, a ich elektryczne i magnetyczne oddziaływania będą wpływały na otaczające je pola.
W oddziaływaniach plazmowych mogą też występować cząstki obojętne, pył, gruz, większe ciała, oraz oddziałują inne siły (grawitacja, lepkość, zderzenia).
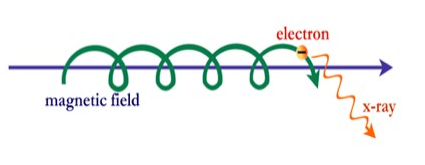
Przylegający do pola relatywistyczny elektron wytwarzający promieniowanie synchrotronowe w paśmie rentgena.
Wspomnieliśmy, że skutki uboczne relatywistycznych elektronów spiralujących wzdłuż linii pola magnetycznego, są często wykrywane w postaci promieniowania synchrotronowego. Z prawa Lorentza wiemy, że musi tam być pole elektryczne równoległe do magnetycznego, a ruch osiowy spiralujących elektronów ze składową prędkości równoległą do pola, jest prądem elektrycznym przyległym do pola. Prąd ten nosi nazwę prądu Birkelanda, występuje on w wielu skalach kosmicznych.
4.4 Inne efekty równań pola
Dobrze jest zapamiętać kilka podstawowych zasad wynikających z zastosowania równań pola elektromagnetycznego.
1. Pole elektryczne wywołuje siłę działającą na każdą cząstkę naładowaną.
2. Siła elektryczna będzie przeciwna dla przeciwnie naładowanych cząstek. A zatem pole elektryczne będzie przeciwnie przyspieszało jony i elektrony, dążąc do ich rozdzielenia. Separacja ładunku w kosmosie jest ważna w fizyce kosmologii plazmy.
3. Pola magnetyczne oddziałują tylko na cząstki będące w ruchu, ze składową prędkości prostopadłą do pola. Ponieważ rezultat zależy od iloczynu wektorowego prędkości i wektora pola, będzie on inny dla różnych kierunków. Skutkuje to zależnym od kierunku oporem elektrycznym. Można to porównać do płynięcia z prądem lub w poprzek rzeki.
4. Kierunek siły magnetycznej zależy od momentu i ładunku cząstki. Jony i elektrony będą wirowały w przeciwnych kierunkach, z innym promieniem i okresem rotacji.
5. Obłok plazmy płynący w poprzek pola magnetycznego spowoduje rozbudowanie się lokalnego pola elektrycznego, które wywoła nowe siły oddziałujące na cząstki naładowane.
6. Zmiany w rozprowadzeniu naładowanych cząstek powodują zmiany w pola elektrycznego pomiędzy nimi. Zmiany pola elektrycznego powodują z kolei zmiany w polu magnetycznym.
7. Równania Maxwella i prawo Lorentza działają razem na zasadzie sprzężenia zwrotnego, zmieniając ruchy cząstek naładowanych i oraz pola.
4.5 Zastąpienie prądów polami magnetycznymi
Powstaje pytanie, czy jest możliwe zastąpienie w równaniach Maxwella prądu elektrycznego polem magnetycznym, celem uproszczenia.
Z technicznego punktu widzenia, odpowiedź jest twierdząca, dla konkretnych sytuacji. Dzieje się tak często w teoriach i modelach magnetohydrodynamicznych, gdyż jest to wygodniejsze do studiowania konkretnych zjawisk plazmowych. Aczkolwiek istnieją zagadnienia w zachowaniu plazmy, gdzie potrzebne, a nawet krytyczne, jest uwzględnienie poruszających się cząstek, gdyż rozważenie po prostu zachowania się pola nie może wymodelować obserwowanej złożoności zjawisk plazmowych.
Sytuacja jest podobna do dualizmu korpuskularno-falowego w fizyce cząstek: istnieją sytuacje, w których należy użyć opisu cząsteczkowego.
Przykłady zachowania plazmy wymagają uwzględnienia opisu cząsteczkowego lub prądowego, w tym komórkowość i włóknistość, transport energii i niestabilności. Rozważenie prądu elektrycznego i obwodów również wymaga opisu cząsteczkowego.
Rozważenie w takich sytuacjach jedynie zachowania pól pomija prawdziwą złożoność zachowania plazmy. Przyjrzymy się niektórym przykładom takiego zachowania.

Galaktyka Centaurus A widziana w świetle rentgena, z centralnym dżetem plazmowym powodującym pióropuszowate struktury, rozciągające się na dziesiątki tysięcy lat świetlnych.
Autor oryginału: Bob Johnson – Jim Johnson
Link do oryginału: http://www.thunderbolts.info/wp/2011/11/04/essential-guide-to-the-eu-chapter-4/