1.1 Dystanse do gwiazd
Kiedy patrzymy w nocne niebo i widzimy gwiazdy, z których wiele jest podobnych do naszego Słońca, wydaje nam się, że leżą one blisko siebie. Ale wcale tak nie jest. Odległości pomiędzy nimi są ogromne.
Odległość to ważna i zarazem trudna sprawa w astronomii. Musimy wiedzieć, jak daleko jesteśmy od gwiazd i galaktyk, ponieważ dużo innych rzeczy w astronomii zależy bezpośrednio od tego – całkowita emitowana energia, masy z ruchów orbitalnych, prawdziwy ruch gwiazd przez przestrzeń i ich rzeczywiste rozmiary.
Gwiazdy są od nas tak daleko, że nawet przez teleskopy są tylko małymi punktami światła. Bez informacji o odległości nie będzie wiadomo, czy patrzymy na małą, ale jasną gwiazdę, czy też na dużą, ale mniej jasną. To samo tyczy się galaktyk, kwazarów, dżetów i innych zjawisk.
Odległość pomiędzy naszymi oczami pozwala nam na posiadanie zmysłu głębi. Każde oko musi być pod specyficznym kątem do obiektu zainteresowania. Mózg interpretuje owe kąty i dostosowuje punkt skupienia, dając nam poczucie, jak blisko lub daleko jest od nas dana rzecz. Tworzy wokół nas trójwymiarowy obraz. Owa biologiczna, kątowa detekcja jest podstawą metody wyliczania odległości, która w astronomii nazywa się paralaksą.
Triangulacja, albo trygonometryczna paralaksa, jest bezpośrednim sposobem użycia dwóch kątów z dwóch pozycji do wyznaczenia odległości od obiektu. Obserwując pozycję gwiazdy na tle dalszych gwiazd z przeciwnych punktów na naszej orbicie okołosłonecznej, mamy szeroką linię bazową, która pozwoli nam zmierzyć różnicę kątów pomiędzy pomiarami oddalonymi o 6 miesięcy, i zmierzyć odległość do czegoś tak dalekiego, jak gwiazda.
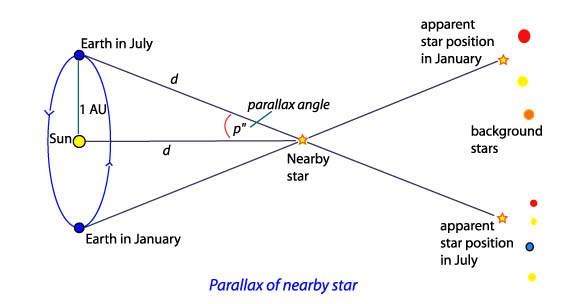
Diagram trygonometrycznej paralaksy – uprzejmość Australian Telescope Outreach and Education website
Ziemia znajduje się w przybliżeniu 93 miliony mil od Słońca, wiec jej orbita jest prawie kołowa. W astronomii odległość ta jest zwana jednostką astronomiczną (ang. AU). Tak więc odległość pomiędzy przeciwnymi pozycjami Ziemi na orbicie wynosi 2 AU, lub około 186 mln mil. Gdy mierzymy kąt do najbliższej gwiazdy (Alfy Centauri) z jednego punktu na orbicie, czekamy 6 miesięcy i mierzymy ponownie, odkrywamy, że różnica jest raczej mała, co wymusza ogromną precyzję pomiarów. Więcej o paralaksie obliczaniu odległości tutaj i tutaj.
Europejska Agencja Kosmiczna (ESA) wystrzeliła swojego automatycznego satelitę teleskop Hipparcos, aby zmierzyć odległość do przeszło 118 000 gwiazd, podczas czasu jego funkcjonowania w latach 1989-1993. Misja: poprawić precyzję skatalogowanych odległości wielu gwiazd i uaktualnić katalogi Tycho i Tycho 2. Z nowymi pomiarami paralaksy, 20 870 gwiazd spełniło kryterium błędu paralaksy mniejszego 10%.
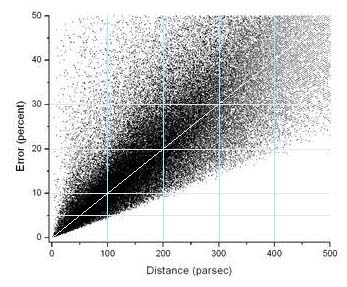
Wykres błędu paralaksy z satelity HIPPARCOS, sporządzony przez Ralfa Bigga, z katalogu danych ESA/HIPPARCOS. Zwracamy uwagę na rosnący procent błędu (pionowo rosnący klin) w stosunku do odległości.
Nawet z bliższymi prawdy danymi satelitarnymi, odległości do gwiazd do około 200-220 lat świetlnych mają do 10% błędu i są coraz mniej dokładne aż do około 500 lś. Za tą granicą, pomiary trygonometryczną paralaksą nie nie powinny być traktowane z zaufaniem. Pogge, w linku do swojego piątego wykładu, twierdzi, że dane z Hipparcos „dają dobre odległości do 1000 lś.”, a jednak przybliżony dystans zaledwie 500 lś, obarczony błędem 20%-30%, jest zbyt daleki od prawdy, żeby być użytecznym. 1000 lś to niemal niepojęty dystans, a to zaledwie 1% drogi przez Drogę Mleczną.
Kąt 1 stopnia jest dzielony na 60 minut (60′) kątowych. Podobnie minuty dzielą się na sekundy (1′ = 60”) kątowe. Paralaksa do wszystkich gwiazd z wyjątkiem Słońca jest mniejsza niż jedna sekunda. I tak, paralaksa do Alfy Centauri wynosi około 0,75 sekundy, lub około 0,0002 stopnia. Kąt paralaktyczny do wszystkich innych gwiazd jest nawet mniejszy od tej znikomej wartości.
Jeden rok świetlny, dystans, który światło w próżni przebywa w jeden rok, wynosi prawie 60 mln mil. Jeśli podzielisz 3,26 przez paralaksę do gwiazdy w sekundach kątowych, otrzymasz dystans do gwiazdy mierzony w latach świetlnych. Astronomowie generalnie wolą raczej parseki (pc) niż lata świetlne, nawet pomimo, że paralaksa może dostarczyć ścisłych danych dla stosunkowo niewielkich odległości od Słońca.
Przykład: (3,26 / 0,75 sek. kąt.) = 4.36 lat świetlnych, co daje 25,65 trylionów mil lub 1,33 parseków do najbliższej gwiazdy.
Zacznijmy bliżej domu.
1.2 Modelowanie odległości wewnątrz oraz w pobliżu Układu Słonecznego
Robert Burnham sporządził model, aby pokazać nam w znanych pojęciach, jak wiele przestrzeni znajduje się pomiędzy gwiazdami. Aby zrozumieć tą skalę potrzebujemy znać kilka rzeczywistych odległości.
Jak wspomniano wyżej, odległość Ziemi od Słońca to około 92 960 000 mil (149 605 000 km), z reguły zaokrąglana do 92 mln mil (150 mln km). Ten dystans zwany jest jednostką astronomiczną (AU).
Rok świetlny jest równy 63 294 AU. Zbiegiem okoliczności jest to prawie taka sama liczba, jak ilość cali w mili statutowej, 63 360. Co za tym idzie, jest mniej więcej tyle samo cali w 1 AU, ile mil w roku świetlnym. To są na prawdę duże liczby. Pozostańmy przy calach.
Burnham ustalił skalę swojego modelu na 1 cal (1”) równy 1 AU, lub 93 mln mil. 1 mila w naszym modelu oznacza 1 rok świetlny. Skala ta wyraża się jak 1:6 000 000 000 000. Jedna jednostka wyraża sześć milionów milionów jednostek, czyli jeden do sześciu trylionów lub 1:6×1012
Zacznijmy opisywać miniaturowy model Burnhana naszego Układu Słonecznego przy pomocy tej skali. Wiemy, że odległość ziemi od Słońca (1 AU) wyniesie 1 cal. Jak wielkie będzie Słońce? Jego średnica wynosi 870 000 mil, więc w naszym modelu Słońce będzie mierzyć nieco poniżej 1/100 cala. To bardzo mały punkcik. Ziemia będzie w odległości 1 cala, lecz tak mała (0,00009”), że do jej zobaczenia potrzebowalibyśmy mikroskopu.
Promień orbity Plutona wynosi 39,5 raza promień orbity Ziemi, a więc Pluton będzie 39,5 cali, prawie jeden metr, od Słońca.
Heliosfera, region wokół Słońca, w którym dominuje wiatr słoneczny, mierzy jakieś 7 stóp w naszym modelu.
A gdzie w naszym modelu jest najbliższa gwiazda? Najbliżej nas jest Alfa Centauri, oddalona o 4 lś. To więcej, niż 4 mile w naszym modelu.
Tak, 4 mile. Nasz model Układu Słonecznego jest małą plamką, a do drugiej plamki mamy 4 mile. Pomiędzy jest sporo przestrzeni. Jak wielka jest nasza galaktyka w tym modelu? Będzie miała 100 000 mil średnicy. Cienki dysk i ramiona będą grube na tysiące mil. Zgrubienie centralne będzie miało 6000 mil od spodu do wierzchu. Ale nasza galaktyka jest tylko jedną z setek miliardów galaktyk, widocznych we wszechświecie przy pomocy naszych obecnych instrumentów. Nocne niebo wydaje się być zatłoczone gwiazdami, ale gwiazdy są z reguły oddzielone od siebie odległością 10 mln razy większą od własnej średnicy.
1.3 Odległość i grawitacja
Zapamiętajmy, że, jak powiedział Newton, siła grawitacji maleje z kwadratem odległości pomiędzy obiektami. Tak więc przyciąganie się dwóch punkcików odległych o 4 mile nie jest takie duże. Podobnie będzie z dwiema gwiazdami odległymi o 4 lata świetlne. Wykorzystajmy równanie Newtona do policzenia tej siły.
W prostym równaniu poniżej, nad arkuszem obliczeniowym, F jest siłą w Newtonach, G jest bardzo małą liczbą zwaną Stałą Grawitacji, M1 i M2 są danymi masami dwóch gwiazd w kilogramach a r jest odległością pomiędzy ich środkami w metrach. Astronomowie używają systemu metrycznego, lub SI, gdyż jest szerzej używany i wygodniejszy, niż tradycyjny imperialny cali, stóp, mil, funtów i uncji. Aczkolwiek rezultat końcowy jest przedstawiony na dole w postaci siły grawitacji na powierzchni Ziemi, zwanej „gee” (dla grawitacji), niezależnie od systemu miar.
F = G × (M1 × M2) ÷ r²
| Jednostki w metrach, kilogramach, sekundach, jakich zwykle używa się w obliczeniach naukowych | |||
| Odl. Słońca do A. Centauri A+B, d = | 4,395 | lś | 9,4608E+15 m/lś |
| … | 41 580 216 000 000 | m | ze Słońca do A. Centauri |
| M1, masa Słońca: | 1,99E+30 | kg | |
| M2, masa Centaurus A+B: | 3,88E+30 | kg | |
| Stała grawitacji, G = | 6,67428E-11 | ||
| Iloczyn mas (M1 · M2): | 7,72E+60 | kg2 | |
| Kwadrat odległości (r2): | 1,73E+33 | m2 | |
| F = G × (M1 × M2) ÷ r² | Siła grawitacji Newtona pomiędzy dwoma masami w odległości r | ||
| Siła działająca na Słońce, F: | 2,98E+17 | N | |
| „gee” – grawitacja na powierzchni Ziemi, równa przyśpieszeniu 9,8 m/s2 | |||
| F = ma | |||
| Przekształcając, aby otrzymać przyspieszenie a = F / m: | 1,5E-13 | m/s2 | |
| Dzieląc przez przyspieszenie ziemskie, 9,8 m/s2 | 1,528E-14 | przyspieszenia ziemskiego w centrum Słońca | |
A zatem układ podwójny Alfy Centauri wywiera na Słońce siłę jednej 153-trylionowej przyciągania ziemskiego.
Pomimo swojej ogromnej masy, te dwie gwiazdy wywierają na siebie tylko niewielkie przyspieszenie. Jakakolwiek siła kontrolująca zachowanie materii musi być dość silna i musi oddziaływać efektywnie na ogromne odległości.
Prawo grawitacji Newtona wystarczy do opisania sił przyciągania wewnątrz naszego układu słonecznego. Ale relatywnie słaba grawitacja mogłaby tylko działać efektywnie, jeżeli w ogóle, na przestrzeni międzygwiezdnej, gdyby prawdą było, że przestrzeń jest pusta i nie ma alternatywnych sił, mogących przezwyciężyć grawitację.
Autor: Bob Johnson – Jim Johnson
Link do oryginału: http://www.thunderbolts.info/wp/2011/09/02/essential-guide-to-eu-chapter-1/

