Zdjęcia galaktyk i ich rdzeni, uzyskane dzięki obróbce cyfrowej, pokazują, że czarne dziury nie są mitem. Okazuje się jednak, że nie funkcjonują one ściśle według modeli opracowanych przez teoretyków, a zatem konieczna jest praca obserwacyjna i refleksyjna. Pomysły i hipotezy, które tu proponujemy, to tylko robocze tropy. Należy zatem rozważać je z rozwagą i otwartym umysłem.
Bernard Lempel, 26 września 2001 r.
Teoretycy zaproponowali dwa modele czarnych dziur
- Sferycznie symetryczna czarna dziura
To właśnie ten model, niesłusznie, jest zawsze prezentowany. Nie będę o nim pisał, ponieważ model ten ma przeciwko sobie dwa argumenty, które zdecydowanie go podważają. Pierwszym jest to, że każdy masywny obiekt (gwiazda), który się zapada, zachowuje nieuchronnie swój moment kątowy, a zatem zawsze kończy jako relatywistyczna wirująca czarna dziura. Jednak, jak udowodniono, we wszechświecie nie istnieją gwiazdy, które nie obracają się wokół własnej osi. Drugim jest pojawienie się „osobliwości” pod postacią nieskończoności gęstości, która jest fizycznie niedopuszczalna. - Czarna dziura z osią symetrii. (Czarna dziura Kerra)
Ten model wydaje się znacznie bardziej zbliżony do fizycznej rzeczywistości. Uwzględnia on konsekwencje wynikające z momentu pędu gwiazdy. Opisuje wiarygodny relatywistyczny stan końcowy. Niestety opisuje on tylko wywnioskowany wynik końcowy, ale nie to, co naprawdę dzieje się podczas kolapsu, co może znacznie zmodyfikować ten stan końcowy. Z drugiej strony nie rozwiązuje on również problemu „osobliwości” występującej w czarnych dziurach o symetrii sferycznej. Są to powody, które zmuszają do ponownego przyjrzenia się temu modelowi.
Komentarz: Podkreślmy ten punkt, nie mówimy tutaj o „matematycznej osobliwości”, ale o wielu fizycznych osobliwościach.
Rewizja czarnej dziury Kerra, kilka hipotez. (KBHR)
1. Kolaps.
Podczas zapadania się masywnej gwiazdy, ze względu na zachowanie momentu pędu, kątowa prędkość obrotowa gwiazdy przyspiesza tak, że prędkość na równiku dąży do maksymalnej prędkości „C”. (prędkość światła # 300.000 km/s)
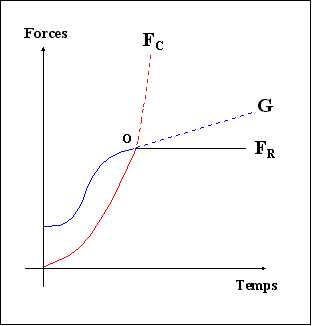
2. Efekty inercyjne.
Po osiągnięciu prędkości maksymalnej (O) następuje równowaga (FR) pomiędzy siłami grawitacyjnymi (G) i odśrodkowymi (FC). Te ostatnie mają tendencję do zwiększania się w nieskończoność (funkcja relatywistyczna), podczas gdy siły grawitacyjne mają tendencję do bycia globalnie stałymi, ponieważ są bezpośrednio związane z masą, a geometria jest ograniczona w najlepszym przypadku jako kula.
Kolaps zostaje wówczas zatrzymany.
Na całej długości kolapsu i na zewnątrz równika fizyka jest zgodna z klasycznymi prawami mechaniki. Tak więc siła odśrodkowa, wynikająca z bezwładności, jest skierowana, od osi obrotu, na równik. W rezultacie materia, cała materia, jest wyrzucana w kierunku równika, gdzie gromadzi się w kształcie relatywistycznego rozdarcia.
W szczelinie tej i tylko w niej siła odśrodkowa jest skierowana do wewnątrz. (efekty relatywistyczne). Mamy zatem w rozdarciu efekt zawężania. Zauważmy, że materia ma wtedy kształt plazmy cząstek o bardzo dużej gęstości (neutrony, protony, elektrony itp.). Zauważmy jednak, że model ten nie implikuje, że gęstość jest nieskończona.
Właśnie zobaczyliśmy, że bezwładność ma do odegrania bardzo dużą rolę w czasie formowania KBHR. Ale jej rola na tym się nie kończy. Bezwładność jest bezpośrednio związana z masą. Moment bezwładności jest bezpośrednio związany z prędkością kątową rotacji rozdarcia. Wynika z tego, że im masywniejsza czarna dziura, tym bardziej zachowuje się jak absolutnie inercyjna platforma. Jej oś obrotu nie może zmienić się w żaden znaczący sposób w czasie. Jest to „quasi-idealny” relatywistyczny żyroskop. W przyszłości będzie można doskonale wykorzystać tę właściwość hipermasywnych czarnych dziur znajdujących się w niektórych rdzeniach galaktyk jako odniesienia do mapowania wszechświata. (Na przykład M 87).
Moment bezwładności jest taki, że wszelkie „próby” jego modyfikacji są skazane na niepowodzenie. Tak więc akrecja materii przez gwiazdę nieuchronnie pociąga za sobą wyrzucenie równoważnej masy z KBHR. Gdyby tak nie było, KBHR eksplodowałby. Jest to tym bardziej prawdziwe, gdy stosunek momentów bezwładności między czarną dziurą a gwiazdą jest większy. Zauważmy, że w tym przypadku wyrzut może nastąpić tylko w płaszczyźnie rotacji. Ta właściwość implikuje, że KBHR są całkowicie ustabilizowanymi obiektami, a ich masa jest niezmienna, gdy tylko ich równik osiągnie graniczną prędkość.
3. Pola magnetyczne
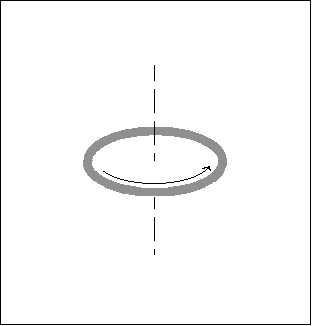
Zobaczyliśmy, że KBHR prezentuje się pod postacią rdzenia plazmowego w rotacji relatywistycznej i zbudowanego z cząstek o bardzo dużej gęstości. Jeśli niektóre z tych cząstek są naładowane, wówczas można uznać, że jest to nadprzewodnik poddany działaniu ogromnego prądu elektrycznego, ponieważ jest on wzmacniany zgodnie z zależnością:
W związku z tym płaszczyzna rdzenia jest przecinana przez niezwykle intensywne pole magnetyczne. Ale uwaga, to nie naładowane cząstki krążą w materii, to torus, innymi słowy, jest to materialna podpora, która jest w rotacji i która niesie ze sobą naładowane cząstki.
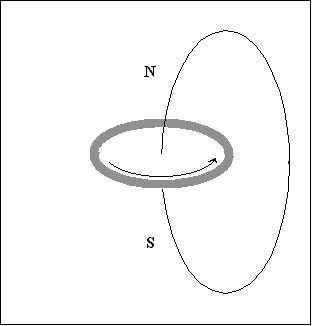
Wynikiem tej cechy jest to, że pole magnetyczne również znajduje się w relatywistycznej rotacji, w stosunku do swojej osi. Linie pola magnetycznego przecinają płaszczyznę obrotu KBHR o promieniu zewnętrznym większym niż promień równika rozdarcia (Czarnej Dziury). Diagram obok przedstawia ścieżkę jednej z tych linii pola.
Ze względu na ograniczenie maksymalnych osiąganych prędkości, różnica obrotów kątowych φ (różnica fazy) między punktem znajdującym się na równiku KBHR a punktem znajdującym się na linii pola w tym samym planie jest w przybliżeniu równa:
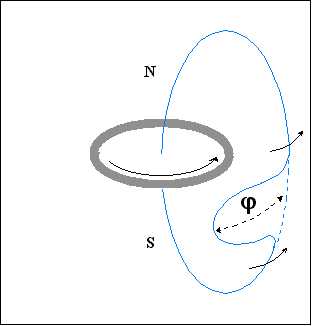
Efektem na poziomie płaszczyzny obrotu jest zniekształcenie każdej linii pola proporcjonalne do tej różnicy fazy. Efekt ten kumuluje się podczas obrotu KBHR. Tak więc, gdy naliczona faza osiągnie:
tj. całkowitego obrotu względnego, wówczas mamy do czynienia z rekombinacją każdej początkowej linii sił w kształt dwóch wynikowych linii pola w płaszczyźnie obrotu. Fragmenty początkowych linii pola aksjopolarnego również ulegają rekombinacji. Proces ten kontynuowany jest w nieskończoność, a jego końcowym rezultatem jest uzyskanie toroidalnego pola magnetycznego w płaszczyźnie rotacji KBHR. Jest to odpowiednik tokamaka, chociaż nie jest on uzyskiwany w taki sam sposób, jak ten, który jest używany przez fizyków do uzyskiwania energii termojądrowej pewnego dnia. To pole magnetyczne, wraz z polem elektrycznym, są w stanie wyrzucić z KBHR naładowane cząstki (protony i elektrony) i zgromadzić je w postaci zjonizowanej plazmy w polu magnetycznym, która jest następnie utrzymywana przez te cząstki. Zauważmy, że z jednej strony, grawitacja nie ma żadnego znanego bezpośredniego wpływu na pole magnetyczne, a z drugiej strony, że w skali atomowej grawitacja jest słabą siłą w porównaniu z siłą elektromagnetyczną.
4. Toroidalne pole magnetyczne złączone z dipolowym polem magnetycznym.
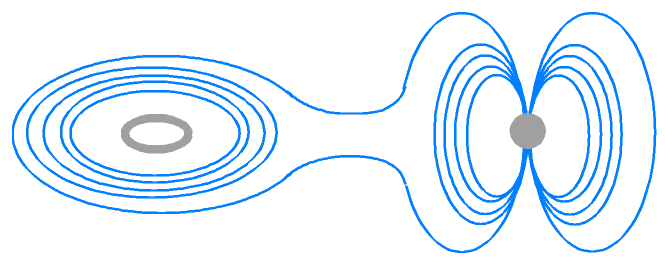
Może się zdarzyć, że środowisko magnetyczne KBHR jest pod wpływem pola magnetycznego obiektu takiego jak czarna dziura, magnetar lub gwiazda neutronowa. W zależności od sytuacji te powiązane pola mogą być toroidalne lub dipolarne. Rekombinacja linii pola w przestrzeni pośredniej umożliwia powstanie skupionego pola magnetycznego. Właściwość ta jest niezbędnym warunkiem formowania się aksjoplanarnych dżetów, takich jak ten, który został zaobserwowany w galaktyce M 87.
5. Wyrzut materii.
Zauważyliśmy, że z powodu niezmienności masy KBHR jest w stanie wyrzucać materię w swojej płaszczyźnie obrotu. Ale ta materia może składać się tylko z neutronów, które bombardują porus plazmy, ze wszystkimi wynikającymi z tego konsekwencjami fizycznymi. Jeśli temperatura plazmy jest niższa niż 2 MeV, zachodzące procesy jądrowe umożliwiają rekombinację cząstek, czego wynikiem jest ciągła pierwotna nukleosynteza.
6. Obserwacje

Obraz jądra galaktyki M 87 uzyskany w wyniku cyfrowej obróbki zdjęcia wykonanego przez ESO na VLT jest być może dobrą wskazówką, że rozważane hipotezy odpowiadają rzeczywistości. Zauważmy, że rozprzestrzenianie się rąbka plazmy jest obrazem rozprzestrzeniania się linii pola w płaszczyźnie rotacji KBHR.
7. Mechanizmy akrecji. Inne hipotezy.
KBHR to obiekt o masie kilku mas Słońca. Po jego narodzinach można rozważyć dwa przypadki.
- Jeśli urodził się w środowisku ubogim w materię, KBHR pozostanie w takiej formie przez nieokreślony czas.
- Z drugiej strony, jeśli narodziła się ona w środowisku bogatym w materię, gazy i gwiazdy, wówczas uruchomiony zostaje mechanizm akrecji materii w kierunku KBHR. Jednak ze względu na niezmienność masy ta sama ilość masy jest wyrzucana. Ta akrecja/wyrzut zwiększa globalną masę układu. Dlatego coraz więcej materii jest akreowane. I coraz więcej masy jest wyrzucane. Mamy więc do czynienia z prawdziwym samoindukującym się zjawiskiem lawinowym. Jest to zjawisko systemowe z dodatnim sprzężeniem zwrotnym. Gdy zjawisko się rozpocznie, nigdy się nie zatrzyma. Jedynym ograniczeniem jest globalna ilość dostępnej materii. To właśnie ten mechanizm pozwala na recykling materii, dlatego jest wieczny. Pojawia się zatem niezwykle proste pytanie: Gdzie znajduje się główna część masy KBHR?

- Tylko w toroidalnej czarnej dziurze?
- W akreowanej materii?
- W wyrzucanej materii?
- W torusie plazmy?
Odpowiedź jest prosta. Masa rozkłada się na całość tych elementów. Proporcje są zaskakujące. Ponad 99% masy rozkłada się pomiędzy materię w akrecji i materię wyrzucaną. KBHR jest tylko początkiem samoindukującego się zjawiska lawinowego. Jak tylko zjawisko zostanie zapoczątkowane, gdybyśmy stłumili czarną dziurę, zjawisko trwałoby nadal, ponieważ izolowana masa czarnej dziury jest znikoma w porównaniu z akreowaną/wyrzucaną materią.
Być może galaktyki rodzą się w ten sposób. Co więcej, nic nie stoi na przeszkodzie, aby czarna dziura, inicjator zjawiska, została wyrzucona ze swojej centralnej pozycji, a także, aby czarna dziura nie była masą orbitującą wokół masy akreowanej. Lub też, że czarna dziura może zostać złapana w wysokoenergetyczny strumień pochodzący z centrum galaktyki, jak pokazano na ogólnym widoku M 87.
Wnioski:
- Magnetyzm jest w stanie generować „wąsy” wokół KBHR.
- Magnetyzm pozwala na wyrzucenie naładowanej materii. Równowaga mas nie jest bez znaczenia!
- Bezwładność, w ramach demonstracji siły odśrodkowej, pozwala na wyrzucenie materii z KBHR (neutronów).
- Hiper masywne czarne dziury są układami samoregulującymi się. Jeśli materia jest gromadzona, ta sama ilość materii jest wyrzucana.
- Czarne dziury są układami wchodzącymi w interakcje z otoczeniem. Nie możemy traktować ich jako odizolowanych obiektów.
- KBHR rdzeni galaktyk są samoutrzymującymi się systemami lawinowymi.
- KBHR są fabrykami recyklingu materii. Zapewniają one stałą „pierwotną” nukleosyntezę.
Natężenia niektórych znanych lub przypuszczalnie znanych pól magnetycznych:
| Obiekt | Intensywność (gausy) |
| Ziemia | 0,6 |
| Zwykły stały magnes | 102 |
| Najsilniejszy magnes stały (laboratoryjny ) | 105 |
| Najsilniejszy magnes ulotny (laboratoryjny) | 107 |
| Najsilniejsze w zwykłej gwieździe | 106 |
| Typowe w pulsarach radiowych | 1012 |
| Typowe w magnetarach | 1015 |
| Czarna dziura | 1020? |
Dalsza lektura:
- Kość w modelu akademickim
- Kość w czarnej dziurze
- Niniejsza strona w formacie PDF (210 kB)
- Gradienty jasności w jądrze M87 (B. Lempel) (franc.)
- Kinematyka w sercu M 87 – V02 (B. Lempel) (franc.)
Inne dokumenty:
- Kwazary; interpretacja supermasywnej rotującej toroidalnej czarnej dziury. R. J. Spivey. (Model toroidalnej czarnej dziury Kerra, wiarygodny, ale niekompletny z punktu widzenia magnetyzmu)
- Elektromagnetyczna ekstrakcja energii z czarnych dziur Kerra. R.D. Blandford, R.L. Znajek.
- XMM-EPIC obserwuje MCG-6-30-15: Bezpośredni dowód na ekstrakcję energii z wirującej czarnej dziury? Jörn Wilms et all.
- Międzyplanetarne pole magnetyczne (IMF)
(Szczególnie interesujące będą zniekształcenia pola magnetycznego związane z rotacją Słońca). - „Magnetary”, miękkie przekaźniki gamma i bardzo silne pola magnetyczne. (Robert Duncan) (ang.)
- Połączyć Słońce z gwiazdami: w kierunku rozwiązania zagadki magnetycznego Słońca? (CNRS – INSU) (franc.)
- Toroidalne kontra biegunowe pola magnetyczne w gwiazdach podobnych do Słońca: próg rotacji. P. Petit et al.
Ostatnie doniesienia:
- 25 marca 2009: Potwierdzenie przez Chandrę, że czarne dziury mogą same się regulować.
- 20 czerwca 2013: Trochę materii wyrzuconej przez czarną dziurę:
Pyłowa niespodzianka wokół olbrzymiej czarnej dziury. (NGC 3783) §
Zobacz także:
Pył w obszarze polarnym jako główny czynnik przyczyniający się do emisji w podczerwieni aktywnych jąder galaktyk. (NGC 3783) - 4 Czerwca 2014: Analiza fal radiowych pochodzących z czarnych dziur pokazuje nieoczekiwaną obecność długo zaniedbywanych pól magnetycznych. – Zaskakująco silne pola magnetyczne podważają siłę przyciągania czarnych dziur §
Ostatnie wydanie: 06/22/14
Autor: Bernard Lempel
Przetłumaczono z: Re-examined Kerr Black Hole
