Ruch translacyjny jest jednym z rodzajów ruchu mechanicznego ciał w przestrzeni. Ruch taki może być jednostajny lub przyspieszony.
Transfer jest bardziej precyzyjnym pojęciem, zawierającym takie pytania, jak to, co jest transferowane, skąd i dokąd, w czym i względem czego, w jakim rozumieniu i jakim kosztem, jak szybko i jaką drogą.
Transfer może być absolutny, czyli następujący w układzie odniesienia związanym z ośrodkiem falowym, albo może być względny.
Aby utworzyć model pojęciowy procesów biorących udział w ruchu translacyjnym, powtórzmy oryginalne warunki:
- Oscylator (źródło falowe) zawsze poszukuje w ośrodku falowym stabilnej pozycji, w której całkowity wpływ pola falowego będzie zerowy. Miejsce takie nazywane jest dziurą potencjału.
- Ruch dziury potencjału powoduje ruch źródła, a jeśli ruch źródła jest utrudniony, wywiera ono siłę na przeszkodę.
- Jeśli wymuszony transfer źródła falowego nie pociąga za sobą przesunięcia dziury potencjału, źródło opiera się wywieranej na nim sile, z powodu gradientu na polu falowym.
Rozważmy teraz prosty układ z dwoma zgodnymi źródłami falowymi. Odległość między nimi równa jest długości jednej fali stojącej, a dziury potencjałów znajdują się w jej węzłach. Różnica fazy pomiędzy źródłami wynosi zero (Δφ = 0).

Układ taki (il. 96) nie ma potrzeby poruszania się w ośrodku falowym, ponieważ źródła falowe leżą w dziurach potencjału. Oto parametry tego układu:
ν1 = ν2, Δφ = 0, V = 0, l = λst
Nazwijmy ten stan pierwszym stanem kwintesencji.
Aby stworzyć sytuację, w której dziury potencjałów są przesunięte w stosunku do źródeł, wprowadźmy różnicę fazy pomiędzy źródłami (Δφ > 0).

Przesunięcie fazy powoduje zmianę położenia dziur potencjału względem ich pozycji początkowej, a co za tym idzie, przesunięcie źródeł. Źródła są pod wpływem pola falowego, zatem ich naturalną reakcją będzie ruch w kierunku dziur potencjału. Jeśli nic nie blokuje ruchu, źródła będą się poruszać, dopóki nie znajdą się w strefach stabilnej równowagi.
Aby źródła znalazły się w dziurach potencjału z anty-węzłem fali stojącej pomiędzy nimi, układ musi osiągnąć odpowiednią prędkość V.

Istnieje zależność pomiędzy różnicą w fazie, wymiarami i prędkością układu, posiadająca parametry:
ν1 = ν2, Δφ > 0, , l = λst⋅(1−V2/c2).
Układ porusza się jednorodnie, źródła leżą w dziurach potencjału, ale różnica w fazie powoduje żywą falę stojącą pomiędzy źródłami. Nie ma podstaw mówić o wewnętrznych deformacjach wewnątrz układu, ponieważ poruszający się układ jest w stanie wewnętrznej równowagi. Nazwijmy ten stan drugim stanem kwintesencji.
Trzeci stan kwintesencji ma miejsce, gdy przesunięcie fazy pomiędzy oscylacjami źródeł zmienia się w czasie, co powoduje ruch układu ze zwiększającą się prędkością, czyli przyspieszeniem. Sytuacja taka jest znacząca, ponieważ zwiększanie się prędkości układu nie skutkuje kontrakcją w części układu, czyli jest dla niego neutralne, stanowiąc stan spoczynku. Trzeci stan kwintesencji można spowodować sztucznie, a w praktyce ma on miejsce podczas swobodnego spadku w polu grawitacyjnym (pole to, w taki sam sposób, jak opisano, zmienia fazę i częstotliwość elementów ciała).
Rozważmy potoczne przykłady fazowej interpretacji ruchu.
Przykład 1. Dwóch ludzi w łódce rzuca kamienie o równej masie w przeciwnych kierunkach. Jeśli rzucą je równocześnie, łódka pozostanie w spoczynku. Co się jednak stanie, pod warunkiem, że założymy brak tarcia o wodę, jeśli kamienie są rzucane jeden po drugim?

W okresie pomiędzy rzutami, łódka przepłynie, powiedzmy, 100 metrów. Czy po drugim rzucie łódka powróci do pozycji początkowej? Nie, po prostu się zatrzyma. Jeśli powtórzymy procedurę, łódka przemieści się o kolejne 100 metrów, pomimo tego, że rzucono w przeciwnych kierunkach tą samą ilość materii! A teraz załóżmy, że proces ten można dowolnie przedłużać, i że ma on naturę falową, czyli, że nie widzimy jego zachodzenia, oraz nie rejestrujemy utraty masy. Czy ruch łódki nie będzie nam się wówczas wydawał cudem?
W tym przypadku transfer łódki powiązany jest ze specyficznym procesem, mającym komponent fazowo-częstotliwościowo-falowy. W procesach tych następuje tranzyt bez jakiegokolwiek zewnętrznego działania.
Przykład 2. Eksperyment Iwanowa-Didina.

Il. 100. Ruch układu w ośrodku, wywołany różnicą w fazie pomiędzy oscylacjami źródeł.
W obu eksperymentach, pierwszym hipotetycznym, a drugim prawdziwym, ruch osiąga się dzięki różnicy w fazie pomiędzy aktywnymi elementami układu.
Przykład 3.
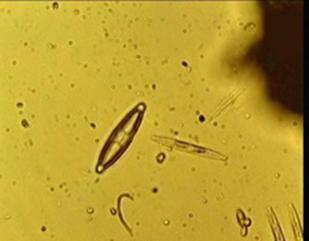
Il. 101. Mikroorganizm zwany naviculae porusza się w swoim środowisku (wodzie) dzięki rozfazowanym oscylacjom swojej kwarcowej powłoki. Jego przybliżona długość wynosi 50 mikrometrów. Zakładając, że długość fali stojącej odpowiada długości mikroorganizmu, wówczas, używając prędkości dźwięku w wodzie (1500 m/s), możemy policzyć generowaną przez nawikulę częstotliwość: 15 MHz.
Wnioski: ruch niekoniecznie zaczyna się na skutek jakiejś zewnętrznej akcji czy siły. Istnieje inny sposób:
Układ źródeł porusza się w ośrodku równomiernie i prostoliniowo, jeśli pomiędzy elementami a ośrodkiem powstaną określone relacje. Charakteryzują się one przesunięciem fazy i zmianami w ośrodku. Zmiany w ośrodku i stałe przesunięcie fazy pomiędzy elementami układu (ciała) nie tylko biorą udział w powstawaniu jednorodnego ruchu, podtrzymują go również.
Oto odwrócona kolejność zjawisk biorących udział w powstaniu warunków i mechanizmu transferu: ruch źródeł → ciśnienie falowe na źródła → przesunięcie dziur potencjału względem źródeł → przesunięcie fazy pomiędzy źródłami. Przyczyną ruchu elementów układu jest tutaj ciśnienie fal, powstające na skutek przesunięcia się dziur potencjału, które następuje na skutek przesunięcia fazy między elementami.
W takim podejściu przesunięcie fazy jest właściwą przyczyną powodująca zmiany w relacjach pomiędzy układu i ośrodkiem falowym, które sprawiają, że układ się porusza. Ruch układu jest konsekwencją lub reakcją na zmiany, jakie zaszły w relacjach między elementami a ośrodkiem.
Należy podkreślić, że pole fal, spajające układ, jest integralną częścią układu, więc każde zmiany w polu fal nieuchronnie prowadzą do reakcji na te zmiany zarówno od części elementów, jak i układu jako całości.
Przychodzą tu do głowy słowa Arystotelesa: …materia niebiańska (ciała) ma skłonność do opierania się file, której potrzebuje do zachowania ruchu.
W przypadku opisanego modelu, to przesunięcie fazy pomiędzy elementami układu powoduje tą skłonność do oporu wobec siły. Zgodnie z Rytmodynamiką, nie ma ruchu poprzez bezwładność, ale jest iluzja takiego ruchu. Ruch poprzez bezwładność jest osiągany przez obecność przesunięcia fazy, zachodzi ze stałą prędkością i w stanie wewnętrznej kwintesencji (synchroniczności). Gdy wyeliminuje się przesunięcie fazy (Δφ = 0), ruch ustaje.
W celu podtrzymania ruchu, potrzebny jest jednoczesny co do kierunku i prędkości transfer aktywnych elementów i dziur potencjału. Należy więc zapewnić synchroniczność (rezonans) pomiędzy ruchem układu, przesunięciem fazy jego elementów i zmianami w polu fal, łączącym te elementy. Osiągnięcie synchroniczności w prostym układzie źródeł z przesunięciem fazy możliwe jest tylko, jeśli porusza się on wg zasady:
- (4.01)
Gdy ten warunek jest niezachowany, synchroniczność jest złamana. Aby ją przywrócić, układ zaczyna się poruszać.
Yuri N. Iwanow
Rytmodynamika – 4.02
Przetłumaczono z http://rhythmodynamics.com/rd_2007en.htm#4.02