Fala stojąca w ruchomym ośrodku

Wyprowadzenie równania fali stojącej w układzie ruchomym względem ośrodka:

$E=E_{\mathrm{padania}}+E_{\mathrm{odbicia}}$

$E_{\mathrm{pad}}=E_0\cdot cos\left(\omega t-k_1\cdot x\right)$

$E_{\mathrm{odb}}=-E_0\cdot cos\left(\omega t+k_2\cdot x\right)$

gdzie

$\omega =2\pi \nu$

$k_1=2\pi \nu /c_1$

$k_2=2\pi \nu /c_2$

wówczas

$E=E_0\left[cos2\pi \nu \left(t-x/c_1\right)-cos2\pi \nu \left(t-x/c_2\right)\right]$

$cosA-cosB=2sin\frac{A+B}{2}\cdot sin\frac{A-B}{2}$

$E=2E_{0}sin\left\{2\pi \nu \left[t-\frac{x\left(c_2-c_1\right)}{2c_1{c}_2}\right]\right\}\cdot sin\left\{\pi \nu \left[\frac{x\left(c_2+c_1\right)}{c_1{c}_2}\right]\right\}$

$E=2E_{0}sin\omega \mathrm{t’}\cdot sin\mathrm{k’}t$

gdzie

$\mathrm{t’}=t-\frac{x\left(c_2-c_1\right)}{2c_1{c}_2}$

 

$\mathrm{k’}=\frac{\pi \nu \left(c_2-c_1\right)}{c_1{c}_2}$

(2.31)

ale

${\lambda }_{\mathrm{st}}=\pi /\mathrm{k’}$

wówczas

${\mathrm{\lambda ’}}_{\mathrm{st}}=\frac{c_1{c}_2}{\nu \left(c_1+c_2\right)}$

(2.311)

ale

$c_1=c\sqrt{1-{\beta }^2{sin}^2\theta }-Vcos\theta$

$c_2=c\sqrt{1-{\beta }^2{sin}^2\theta }+Vcos\theta$ (patrz: wyprowadzenie poniżej)

Kładąc c₁ i c₂ w wyrażenia (2.31) i (2.311) otrzymujemy wyrażenia dla t’ i λ_st dla dowolnej orientacji fali stojącej w ruchomym układzie:

$\mathrm{t’}=t-\frac{V/c^2\cdot x\cdot cos\theta }{1-{\beta }^2}$

(2.32)

${\mathrm{\lambda ’}}_{\mathrm{st}}=\frac{c}{2\nu }\cdot \frac{1-{\beta }^2}{\sqrt{1-{\beta }^2{sin}^2\theta }}$

(3.321)

Przy θ = 0° i λ’_st = λ_st(1−β²):

$\mathrm{t’}=t-\frac{V/c^2\cdot x}{1-{\beta }^2}$

(2.33)

Przy θ = 180° i λ’_st = λ_st(1−β²):

$\mathrm{t’}=t+\frac{V/c^2\cdot x}{1-{\beta }^2}$

(2.34)

Czas przejścia promienia w przód i z powrotem:

$\sum {\mathrm{t’}}_{\parallel }=t-\frac{V/c^2\cdot x}{1-{\beta }^2}+t+\frac{V/c^2\cdot x}{1-{\beta }^2}=2t$

Przy θ = 90° i ${\mathrm{\lambda ’}}_{\mathrm{st}}={\lambda }_{\mathrm{st}}\sqrt{1-{\beta }^2}$ mamy t’ = t.

(2.35)

Przy θ = 270° i ${\mathrm{\lambda ’}}_{\mathrm{st}}={\lambda }_{\mathrm{st}}\sqrt{1-{\beta }^2}$ mamy t’ = t.

(2.36)

Czas przelotu w tą i z powrotem: $\sum {\mathrm{t’}}_{\perp }=t+t=2t$.

Rezultat:

$\sum {\mathrm{t’}}_{\parallel }=\sum {\mathrm{t’}}_{\perp }$

(2.37)

Co oznacza, że:

1. Poruszający się obiekt, złożony z pakietu fal stojących, zmienia swoje podłużne wymiary $1-{\beta }^2$ razy, i poprzecznie $\sqrt{1-{\beta }^2}$, co dokładnie odpowiada kompresji fali stojącej w tych kierunkach.
2. Całkowity czas przejścia promienia tam i z powrotem wzdłuż ramion interferometru Michelsona nie zależy od szybkości urządzenia ani jego orientacji, wynosząc zawsze 2t.
3. Wycinek czasu nie zależy od prędkości układu i jest taki sam we wszystkich jednakowych układach, niezależnie od ich ruchu względem ośrodka.

Wyrażenia te wskazują bezpośrednio na rozwiązanie problemu związanego z ujemnym wynikiem eksperymentu Michelsona. Historycznie, to brak zjawiska, którym można było wyjaśnić wynik eksperymentu doprowadził do przyjęcia Teorii względności i zakleszczenia nauki.

Schemat obliczania prędkości fali względem ruchomego źródła

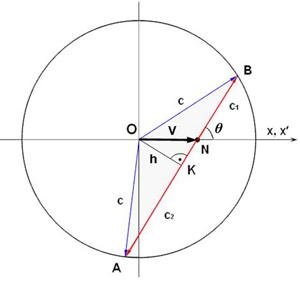
gdzie:

N − poruszające się źródło

V − prędkość źródła

O − współrzędne miejsca emisji fali

c − prędkość frontu fali

c₁ − prędkość frontu fali względem N

c₂ − prędkość frontu fali względem N

Obliczanie prędkości frontu falowego względem źródła

$AK=KB$

$KN=Vcos\theta$

$h=Vcos\theta$

$KB=\sqrt{c^2-h^2}$

$c_1=KB-KN$

$c_2=KB+KN$

Wynik:

$c_1=c\sqrt{1minus;{\beta }^2{sin}^2\theta }-Vcos\theta$

(2.38)

$c_2=c\sqrt{1minus;{\beta }^2{sin}^2\theta }+Vcos\theta$

(2.39)

---

Opiszmy akustyczny eksperyment, potwierdzający poprawność opisanych praw. Istnieje pewien problem z odniesieniem wyników otrzymanych w akustyce do elektrodynamiki. Gdyby nasi poprzednicy (w szczególności Michelson) wiedzieli o kompresji fal stojących w akustyce, być może przeprowadziliby eksperyment nie do pomiaru prędkości w eterze, ale w celu wykrycia kompresji fali stojącej. Innymi słowy, ujemny wynik nie byłby zinterpretowany jako brak eteru, lecz jako potwierdzenie skrócenia ramion interferometru. Teraz wiemy, że eksperyment mający wykryć ruch w eterze luminoforycznym powinien być zaplanowany inaczej.

Eksperyment z dźwiękowymi falami stojącymi

W lecie 1990 przeprowadzono serię eksperymentów z falami dźwiękowymi. Potwierdziły one ponad wszelką wątpliwość, że wraz ze wzrostem prędkości wiatru względem nieruchomego emitera oraz reflektora, ma miejsce ściśnięcie pakietu fal stojących.

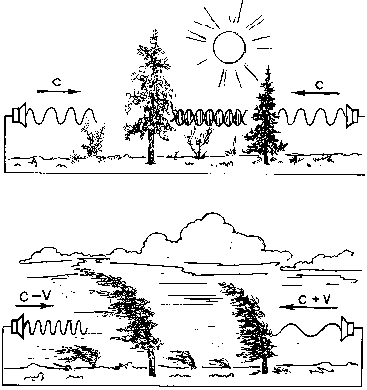
Il. 59. Spokojna pogoda (a) oraz silny wiatr (b). Źródła dźwięku zasilane są z pojedynczego generatora.

Wraz z powstaniem wiatru, długość fal dźwiękowych oraz ich prędkość mienia się zgodnie z efektem Dopplera. Częstotliwość fal w układzie pozostaje stała.

Dla V = konst., θ = 0°

$\nu =\left(c-V\right)/{\lambda }_1$, $\nu =\left(c+V\right)/{\lambda }_2$

(2.40)

Fale o różnej długości, ale równej częstotliwości interferują, dając falę stojącą o długości

${\mathrm{\lambda ’}}_{\mathrm{st}}=c\left(1-{\beta }^2\right)/2\nu$

(2.41)

Dla B = konst. i θ = 90°

$\nu =\sqrt{c^2-V^2}/{\lambda }_{\perp }$

(2.42)

Fale o równej długości oraz częstotliwości interferują, sutkując falą stojącą o długości danej przez:

${\mathrm{\lambda ’}}_{\mathrm{st}}=c\sqrt{1-{\beta }^2}/2\nu$

(2.43)

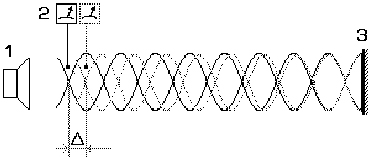
Il. 60. Kluczowy diagram dla eksperymentów z dźwiękiem.

Przy spokojnej pogodzie między emiterem 1 a lustrem 3 powstaje fala stojąca (z reguły eksperyment przeprowadzano podczas spokoju niedługo przed burzą). Dzięki wskaźnikowi 2 rejestrowano węzeł fali stojącej, oznaczonej linią ciągłą. Po powstaniu wiatru rejestrowano przesuwanie się kontrolnego węzła ku lustru 3. Obserwowany efekt interpretowano jako kompresję pakietu fal stojących (pokazanych linią kropkowaną).

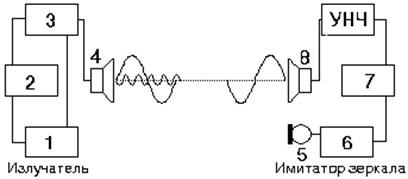
Il. 61. Diagram blokowy urządzenia użytego do eksperymentów: 1 – generator dźwięku, 2 – mnożnik częstotliwości (×4) sterowany pilotem, 3 – mikser, 4,8 – głośniki, 5 – mikrofon do odbioru sygnału z pilota, 6 – dzielnik (:4), 7 – przywracacz oryginalnego sygnału.

Symulator lustra daje możliwość stworzenia pseudo-zgodnego emitera i tym samym rozszerzyć dwojaką bazę eksperymentu, co znaczącą zwiększa czułość urządzenia.

Częstotliwość generatora sterującego nie jest tu istotna. długość fali wynosiła 10 cm, a odległość lustra od głośnika 70 metrów. Przy powstaniu wiatru odnotowano przesunięcie węzła kontrolnego o 5 cm w stronę lustra, co odpowiada wiatrowi o prędkości 30 km/h. Były nawet większe przesunięcia, jednak główna seria eksperymentów pokazała wyraźną zasadę: w przypadku wiatru, pakiet fal stojących się kurczył, niezależnie od tego, czy wiatr wiał wzdłuż, czy w poprzek urządzenia.

Wnioski

Odkrycie kompresji fali stojącej i zastosowanie go do elektrodynamiki obiektów w ruchu w nieruchomym eterze po raz kolejny podnosi kwestię istnienia eteru jako ośrodka falowego.

---

Yuri M. Iwanow

Rytmodynamika – 2.05b

Przetłumaczono z http://rhythmodynamics.com/rd_2007en.htm#2.05