8.1 Plazmowe arkusze prądowe
Omówiono już zwłóknianie arkuszy prądowych. Ta sekcja omawia same arkusze prądowe oraz ich powiązania z polem magnetycznym.
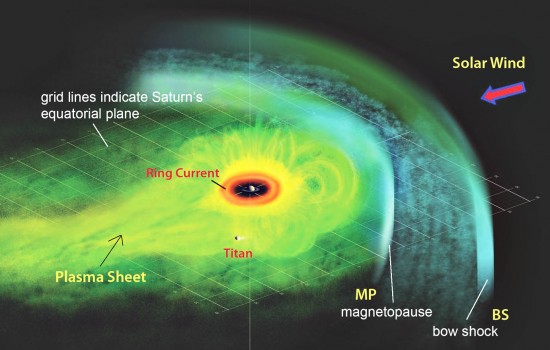
Artystyczna interpretacja plazmowego arkusza Saturna, oparta o dane z instrumentu MII sondy Cassini. Arkusz plazmowy, oddzielający górną i dolną część magnetosfery, zwęża się stopniowo w kierunku zacienionej strony planety. Magnetopauza oznacza przepływ odbitego wiatru słonecznego. Źródło: NASA/Jet Propulsion Laboratory / Johns Hopkins University Applied Physics Laboratory
Arkusz prądowy jest dokładnie tym, o czym mów jego nazwa – cienką powierzchnią, wewnątrz której płynie prąd. Jest to oczywiście różne od rozproszonej chmury poruszających się ładunków lub cylindrycznego włókna prądowego. Arkusz prądowy formuje powierzchnię pomiędzy dwoma obszarami plazmy, podobnie jak warstwa podwójna, i również podobnie jak ona, często rozdziela obszary plazmy o odmiennych charakterystykach.
Prąd w arkuszu płynie w jednym kierunku, zawarty całkowicie wewnątrz arkusza. Można o tym myśleć, że prąd płynie w rozciągniętych wątkach tkaniny lnianej: w każdym rozciągniętym wątku prąd płynie w tą sama stronę, żaden prąd nie płynie w wątkach chmurowych[?]. Prąd zawiera oczywiście poruszające się przeciwbieżnie elektrony i jony, a wiec arkusz zawiera oba rodzaje cząstek.
Oczywiście kierunek prądu może się zmieniać, podobnie, jak sam arkusz nie musi pozostawać płaski. Na przykład, istnieją dowody na istnienie pół-sferycznych arkuszy prądowych na czole „fali uderzeniowej”, gdzie ziemska magnetosfera wchodzi w kontakt z wiatrem słonecznym.
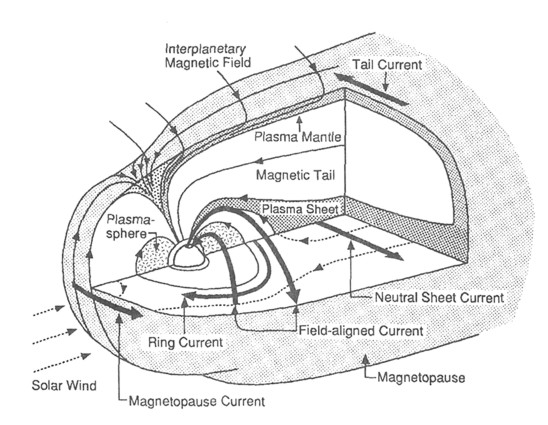
Schematyczny rysunek plazmowych arkuszy prądowych wokół magnetosfery. Źródło: Wikipedia Images, szereg stron bez podania źródła.
Jeśli przeanalizujemy pole magnetyczne w pobliżu arkusza prądowego, odkryjemy, że pole magnetyczne spowodowane przepływem prądu ma odwrotne kierunki po obu stronach arkusza. Jeśli, na przykład, prąd płynąłby w górę tej strony, to nad nią pole magnetyczne miałoby kierunek z lewa na prawo, zaś pod nią – z prawa na lewo, jak można wywnioskować z zasady prawej dłoni dla pojedynczego wątku prądowego (zauważ, że obrót wg zasady prawej dłoni nie jest tym samym, co iloczyn wektorowy zasady prawej dłoni).
Zatem głównym efektem, który wytwarza arkusz prądowy, jest stworzenie osobnych obszarów o przeciwnym polu magnetycznym. W samym miejscu przebywania arkusza prądowego, pole magnetyczne jest zerowe. Dokładnie taka sytuacja ma miejsce w ogonie ziemskiej magnetosfery, gdzie arkusz prądowy jest polem równikowym, rozdzielającym strefy przeciwnego pola magnetycznego. W tym przypadku, plazmowy ogon prądowy płynie azymutalnie, lub „z zachodu na wschód”, a pole magnetyczne jest radialne i przylegające do wewnątrz w północnej półsferze, a zewnętrznie w południowej.
Model grawitacyjny opisuje arkusze prądowe jako spowodowane przez przeciwne pola magnetyczne po każdej stronie. Pamiętając, że pola magnetyczne to pola siły spowodowane ruchem naładowanych cząstek, a więc prądu, okazuje się, że model grawitacyjny odwraca skutek i przyczynę. To, co robi pole magnetyczne wywołane przez prąd, to ściskanie tegoż prądu do postaci arkusza. Nie tworzy zaś samego prądu.
Arkusze prądowe są zatem kolejnym sposobem, na który plazma może przyjmować strukturę komórkową, w odpowiedzi na zróżnicowanie środowiska.
Arkusze prądowe mogą również służyć do przyspieszania masy w impulsowym napędzie plazmowym. Zobacz tekst oraz wideo z Electric Propulsion and Plasma Physics Lab z uniwersytetu w Princeton.

8.2 Prądy prostopadłe
Omówiliśmy już przypadki, gdy prądy płyną równolegle do (są „przyległe do”) pola magnetycznego (włókna i prądy Birkelanda) oraz przypadki, gdy prąd płynie przez obszar pozbawiony pól (arkusze prądowe). Pozostał jeszcze przypadek prądów, które mają składową wektorową prostopadłą do pola magnetycznego, pod wpływem czynników niemagnetycznych działających wraz z polem magnetycznym (patrz sekcja 8.3).
[Przypomnijmy, że F jest wynikowym wektorem siły działającej na naładowaną cząstkę; q oznacza ładunek cząstki; E jest wektorem pola elektrycznego w określonym miejscu i czasie; U jest wektorem prędkości naładowanej cząstki w określonym miejscu i czasie; zaś B to wektor pola magnetycznego w danym miejscu i czasie. Na koniec dodajmy, że pogrubione wektory wiążą się ze skalarnymi wartościami bezwzględnymi plus kierunek, np 3000 km/s na wschód.]
Siła Lorentza działająca na naładowaną cząstkę, F = q(E + U × B) w algebrze wektorów, zależy od korelacji prędkości U cząstki z polem magnetycznym B. Wartość bezwzględną iloczynu wektorowego U × B można zapisać jako UB sin θ, gdzie θ jest mniejszym kątem pomiędzy wektorami U i B. Kierunek siły danej przez U × B jest dana ruchem prawoskrętnej śruby przekręconej z U do B, tj. będącej pod kątem prostym w stosunku do U oraz B.
Powoduje to, że naładowana cząstka poruszająca się prostopadle do pola magnetycznego będzie podążać kołową ścieżką o płaszczyźnie prostopadłej do pola. Możemy to nazwać siłą dośrodkową. Jeśli E jest niezerowe, cząstka będzie również przyspieszać w jego kierunku.
Oczywiście, jeżeli U jest zerowa lub równoległa do pola magnetycznego, siła dośrodkowa nie występuje. Innymi słowy, jeżeli cząstka jest stacjonarna lub porusza się z polem, to nie doświadcza siły magnetycznej.
Zamiast rozważać zmienne kąty pomiędzy U i B, będziemy raczej rozważać osobno składowe U prostopadłe i równoległe do pola magnetycznego. Ponieważ tylko składowa prostopadła jest źródłem siły, skoncentrujemy się na niej. Będziemy również zakładać, że E = 0, o ile nie będzie wprost napisane inaczej.
Prędkość cząstki będąca wynikiem ruchu indukowanego siłą oraz polem magnetycznym, może być rozważana jako ruch kołowy wokół prowadnicy (rysunek poniżej), która podąża za liniami pola magnetycznego z prędkością vp daną równaniem centrum prowadzącego:
vp = (F × B) / qB2
Zauważ, że F jest jakąkolwiek siłą niemagnetyczną (jak np. grawitacja czy pole elektryczne), powodującą ruch cząstki. Ruch ten oddziałuje następnie z polem magnetycznym stosownie do siły Lorentza. Jeśli B jest w kierunku z a F w kierunku y w kartezjańskim układzie współrzędnych, wówczas wynikowa prędkość vp jest w kierunku x.
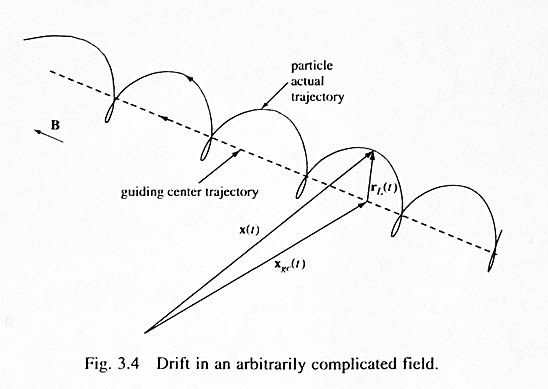
Helikalna trajektoria naładowanej cząstki, z ruchem kołowym nałożonym na ruch dryfu. Źródło: „Fundamentals of Plasma Physics”, Cambridge Press, 2006; Dr. Paul Bellan, California Institute of Technology
To, co mówi nam to równanie, to że gdy cząstka jest pod wpływem zewnętrznej siły prostopadłej do pola magnetycznego, otrzymuje stałą prędkość vp prostopadłą zarówno do siły, jak i do pola. Dzieje się to w sposób następujący:
Jeśli cząstka jest początkowo w spoczynku, siła zewnętrzna (powiedzmy, że pole elektryczne) zacznie ją przyspieszać w swoim kierunku działania, zgodnie z prawem Newtona. Aczkolwiek, gdy tylko cząstka otrzyma drobną składową prędkości prostopadłą do pola magnetycznego, pojawia się siła dośrodkowa, spychająca cząstkę z trajektorii nadawanej jej przez siłę zewnętrzną.
Zewnętrzna siła wciąż stara się przyspieszać cząstkę w kierunku swojego wektora, ale istnieje teraz składowa siły dośrodkowej, przeciwstawiająca się sile zewnętrznej. Przyspieszenie w kierunku zewnętrznej siły zostaje odpowiednio zredukowane.
Pod wpływem pary sił, zewnętrznej i dośrodkowej, cząstka będzie podążać po ścieżce skręcającej o 90 stopni. W miejscu, gdzie ścieżka jest prostopadła do siły zewnętrznej, cząstka osiąga prędkość vp, daną przez równanie prowadnicowe, a siła dośrodkowa, z powodu oddziaływania vp oraz B, doskonale równoważy siłę zewnętrzną.
A zatem nie ma już dłużej przyspieszenia w kierunku zewnętrznej siły, nie ma go również w kierunku wskazywanym przez vp, ponieważ nie działa w tym kierunku żadna siła. Cząstka posiada stałą prędkość prostopadłą zarówno do B jak i do siły zewnętrznej.
Tak długo, jak cząstka porusza się z prędkością vp w kierunku prostopadłym, sytuacja jest stabilna i zewnętrzna siła jest równoważona przez siłę dośrodkową.
8.3 Efekt wielu zewnętrznych sił
Powyższy wywód dotyczy każdej stałej siły zewnętrznej działającej na cząstkę naładowaną w polu magnetycznym. Różne siły mogą powodować ruch prostopadły do pola magnetycznego, włączając w to grawitację, pole elektryczne i bezwładność. Każda będzie wywierała inny efekt w zależności od tego, czy jest funkcją masy, ładunku elektrycznego etc.:
Przypadek A. Siła pola elektrycznego, FE × B, dla pola elektrycznego prostopadłego do B.
Ponieważ FE = qE, więc równanie prowadnicowe przyjmuje postać:
vp = (E × B) / B2
- W przypadku A, poprzeczna prędkość cząstki nie zależy od jej ładunku. Dzieje się tak w specjalnym przypadku, gdy zarówno jony, jak i elektrony dryfują w tym samym kierunku, jak widzieliśmy rozważając skupianie materii przez włókna prądowe.
Przypadek B. Fg × B
Ponieważ Fg = mg, wynikowy dryf poprzeczny jest zależny zarówno od masy, jak i od ładunku cząstki. Dla przypadku B:
vp = (g × B) × m / qB2
- Jony i elektrony poruszają się wówczas w przeciwnych kierunkach, dochodzi więc do przepływu prądu, separacji ładunków i powstania stref przeciwnego potencjału (pola elektryczne). Wszystkie te efekty występują po prostu jako rezultat oddziaływania grawitacji i pola magnetycznego. Oczywiście prowadzi to do kolejnych efektów, przez co mamy do czynienia ze złożonym zachowaniem plazmy (Fundamentals of Cosmic Electrodynamics, Boris V. Somov, Kluwer Academic Publishers, 1994, Chapter 2, Motion of a Charged Particle in Given Fields).
- Dodatkowo zależność pomiędzy prędkością a masą cząstki prowadzi do separacji chemicznej na różne jony, oraz do konwekcji Marklunda.
- Szczególnie interesujący jest tu jeden przypadek poprzeczności. Rozważmy Ziemię i jej pole magnetyczne, które można przedstawić jako zestaw linii rozchodzących się jak segmenty pomarańczy. W płaszczyźnie równikowej, linie ustawione są w kierunku północ-południe. Siła grawitacji będzie natomiast wszędzie promieniście dośrodkowa, a więc w płaszczyźnie równika prostopadła do pola magnetycznego.
- Jakiekolwiek jony i elektrony w sąsiedztwie, na przykład w jonosferze, uzyskują prędkość prostopadłą zarówno do B jak i g, na skutek połączonych oddziaływań ziemskiego przyspieszenia i pola magnetycznego. Ponieważ prędkości jonów i elektronów są przeciwnie skierowane, jest to równoważne z prądem płynącym w pierścieniu w płaszczyźnie równikowej. Pasy Van Allena są przykładem prądów pierścieniowych.

- Jest to nieunikniony rezultat obecności naładowanych cząstek w polu magnetycznym zorientowanym pod kątem prostym do pola grawitacyjnego. Zawsze w takiej sytuacji powstanie prąd. Szereg księżyców Jowisza i Saturna wykazuje obecność takich prądów, na co są dowody w postaci promieniowania elektromagnetycznego powstającego, gdy indukowane w ten sposób prądy wchodzą w kontakt z ich atmosferą w rejonach polarnych.
Case C. Bezwładność, Fi = -m (du/dt) (drugie prawo dynamiki Newtona)
Jest to przypadek, gdy naładowana cząstka posiada już moment bezwładności mu (masa bezwładna razy wektor prędkości), gdy wkracza w pole magnetyczne. Równanie prowadnicowe wyznacza początkowy moment w zależności do pola magnetycznego:
vp = -mq/B2 du/dt × B
Ponieważ vp jest zależne od ładunku, końcowa prędkość elektronów i jonów jest skierowana przeciwnie, tworząc prąd elektryczny. Jony o różnej masie będą miały różną prędkość, zostaną więc chemicznie posortowane. Istnieją też inne ważne efekty:
- Jeśli obszar plazmy jest przyspieszany do określonej prędkości przez, powiedzmy, siłę I × Bktóra przyspiesza przeciwnie poruszające się jony i elektrony w tym samym prostopadłym kierunku, wówczas plazma otrzymuje energię kinetyczną kosztem obwodu prądowego.
- Kiedy obszar poruszającej się plazmy natrafia na inny rejon, w którym może ustanowić nowy obwód w lokalnej plazmie, jego prędkość vp spowoduje powstanie prądu prostopadłego do B oraz vp. Oddziaływanie tego prądu z B spowoduje siłę działającą na poruszającą się plazmę, która ją spowolni. Innymi słowy, energia kinetyczna plazmy służy do wygenerowania prądu w nowej lokalizacji.
- Oddziaływanie siły inercyjnej naładowanych cząstek z polem magnetycznym zamienia energię kinetyczną na elektromagnetyczną. Jest więc sposobem, w który energia może być przeniesiona pomiędzy różnymi miejscami.
8.4 Obwody elektryczne w plazmie
Jeżeli ładunek nie przemieszcza się od elektrostatycznego źródła lub nie zmierza do takowego odpływu, jest częścią zamkniętego obwodu. W przestrzeni kosmicznej nie jest to takie oczywiste, ponieważ przewodnik może być niewidoczny, a zamkniecie obwodu może znajdować się bardzo daleko od badanego obszaru.
Rozważenie obwodów w kosmosie pozwala wyjaśnić takie zachowania, jak transport energii z jednego miejsca do drugiego, co napędza wykrywalną aktywność elektryczną w badanym regionie.
Warto tutaj wspomnieć, że plazma zawierająca jakąkolwiek nieregularność ładunku zaczyna się poruszać względem pozostałych regionów plazmy w polu magnetycznym, wtedy generuje pole elektryczne i prąd w pozostałych rejonach.
Model grawitacyjny uwzględnia ekranowanie Debye’a, występujące jako efekt podobny do otoczki Debye’a wokół naładowanego ciała, ograniczające niezrównoważenie ładunków do długości Debye’a. Aczkolwiek siła v × B z równania Lorentza jest niezależna od długości Debye’a, i mogą indukować pole elektryczne w plazmie daleko poza długością Debye’a.
8.5 Warstwy podwójne jako elementy obwodów
Każda warstwa podwójna przyspiesza jony i elektrony z powodu obecności spadku potencjału. Jeżeli warstwa podwójna przewodzi prąd, wówczas efektywnie tworzy część obwodu elektrycznego. Energia do przyspieszania cząstek jest pobierana przez obwód i przekształcana w warstwie podwójnej w energię kinetyczną.
Warstwa podwójna działa więc jak inercyjny opornik i może doświadczać reakcji dryfu. Jest to analogiczne do odrzutu strzelby, gdy jej źródło mocy przyspiesza nabój. Cząstki przyspieszane przez warstwę podwójną powodują powstanie ciśnień w otaczającej plazmie, z którą oddziałuje, i powoduje promieniowanie. Rozpraszanie nadmiaru energii, które w ten sposób zachodzi, pozwala plazmie zachowywać stan stabilny.
8.6 Energia i indukcyjność
Energia obwodu przekazywana do warstwy podwójnej może brać swój początek w energii zmagazynowanej w polu magnetycznym lub energii kinetycznej obłoku plazmy. W terminologii obwodów, element przechowujący energię nazywa się induktorem. Plazma może więc być traktowana jako taki induktor w prostym obwodzie. Podobnie warstwa podwójna pełni rolę podobną do kondensatora, aczkolwiek ze zmienną charakterystyką – np. z rezystancją malejącą w miarę wzrostu prądu.
Wszystkie obwody elektryczne posiadające indukcyjność są potencjalnie niestabilne, w zależności od wartości woltażu, indukcyjności, oporu i pojemności w obwodzie. Jeśli całkowity opór obwodu jest ujemny, co często zdarza się w plazmie z powodu opadającej charakterystyki prądowo-napięciowej, wówczas stabilność obwodu indukcyjnego jest niemożliwa. Prosty obwód zawierający woltaż, indukcyjność i ujemną oporność będzie albo oscylował, albo rozproszy całą swoją energię i wygaśnie.
Jeżeli spadek potencjału w warstwie podwójnej jest większy niż potencjał plazmy, wówczas warstwa taka jest klasyfikowana jako silna. Silna warstwa podwójna będzie odbijać wszystkie nadchodzące cząstki o energii niższej niż potencjał plazmy. Tylko cząstki o większej energii przedostaną się do warstwy podwójnej i zostaną przyspieszone przez różnicę potencjału wewnątrz niej, czyli przez pole elektryczne.
Zachowanie plazmy w CCDL (prądowej warstwie podwójnej) jest więc zależne od charakterystyki zewnętrznego obwodu, który kieruje powstawaniem CCDL.
8.7 Obwody rezonansowe
Obwód posiadający indukcyjność i pojemność posiada też naturalną, bądź rezonansową częstotliwość na której elektrycznie oscyluje. Podobnie, obwód plazmowy posiadający indukcyjność w formie energii zmagazynowanej w polu magnetycznym, CCDL o ujemnym oporze będzie mieć tendencję do posiadania częstotliwości rezonansowej, wg której energia jest wymieniana pomiędzy polem elektrycznym warstwy podwójnej a polem magnetycznym plazmy. W miarę wzrostu pola elektrycznego w warstwie podwójnej, cząstki przez nie nią przechodzące będą przyspieszane do większych prędkości.
Widać, że ów model jest mechanizmem potencjalnych silnych wybuchów promieniowania o wysokiej częstotliwości. Dla kontrastu, model grawitacyjny próbuje wyjaśnić podobne fenomeny przez postulowanie istnienia super-gęstych gwiazd neutronowych, wirujących z prędkością tysięcy obrotów na sekundę.
Nie wszystkie sytuacje skutkują częstotliwością rezonansową. Obecność wariacji skutkuje często oscylacjami w szerokim spektrum częstotliwości. W terminologii obwodów elektrycznych warstwa podwójna jest wówczas „hałaśliwa”. Efekt szumów polega na stworzeniu elektronów o szerokim zakresie energii, w strumieniu wychodzącym z warstwy podwójnej. Część elektronów posiada dość energii do wyłamania się z pola magnetycznego otaczającego prąd, co prowadzi do rozszerzania się plazmy.
Autor oryginału: Bob Johnson – Jim Johnson
Link do oryginału: http://www.thunderbolts.info/wp/2012/01/17/essential-guide-to-the-eu-chapter-8/